[复材] Abaqus和Tosca优化RVE结构
本文摘要(由AI生成):
本文介绍了一种使用RVE分析方法和Tosca优化技术设计鞋底Lattice结构的方法。首先,通过RVE分析方法研究材料性能,可以直接获取某些均质属性,并通过FE-RVE模型预测更大尺度上的材料性能。接着,使用Abaqus模型创建模型的周期性边界条件,采用MooneyRivlin模型描述超弹性TPU材料。然后,采用最小应变能目标和体积约束进行Tosca优化,优化循环迭代如图3所示,优化结果如图4所示。最后,采用以上流程设计出不同的Lattice结构,如图5所示。
1、RVE分析方法
材料微观结构的代表性体积元(FE-RVE)是以一种不受平均场均质化中使用的分析方法来研究材料性能。某些均质属性(如弹性、热膨胀和电导率)可以直接通过FE-RVE模型获取,另外,还可使用FE-RVE的均质响应代替样片的测试数据,通过研究在给定的远场加载历史中,对某一材料性能进行评估研究,来预测在更大的尺度上的材料性能(如塑性、粘弹性和损伤模型)。
本文采用RVE分析方法结合Tosca优化技术,对图1鞋底的Lattice结构进行设计。

图1 鞋底Lattice结构
2、Abaqus模型
上讲提到的RVE的插件,在此使用其创建模型的周期性边界条件,图2所示,其材料为超弹性TPU材料,采用MooneyRivlin模型。
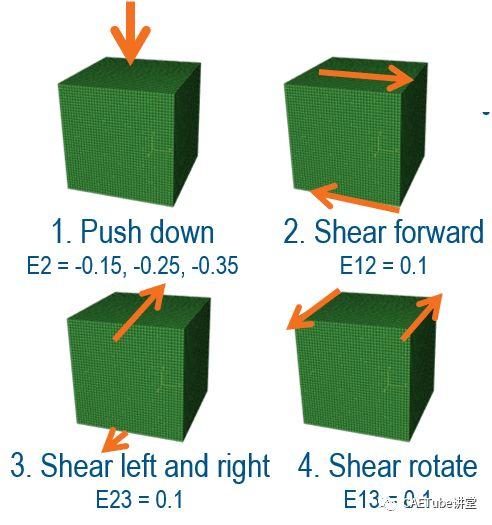

图2 RVE载荷工况
3、Tosca优化
采用最小应变能目标和体积约束,优化循环迭代如图3所示。
图3 优化迭代
优化结果如图4所示。
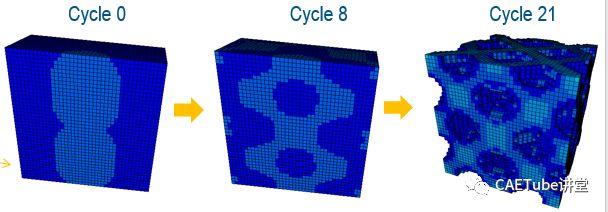

图4 优化结果
4、讨论
采用以上流程,设计出不同的Lattice结构,如图5所示。
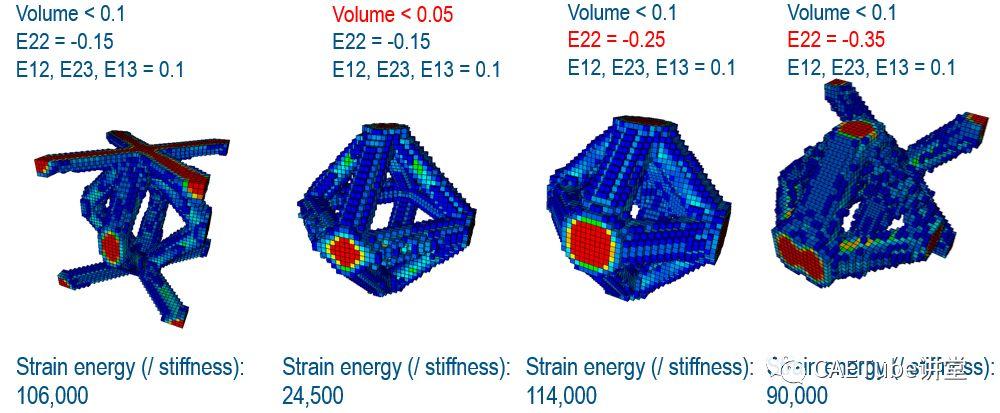
图5 优化结果选择
登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2019-03-16
最近编辑:6月前
相关推荐
最新文章
热门文章






