《线性声学基本现象》Chapter 14 - 声在耗散介质中的传播-Biot理论
MSC软件官方信独家连载的一系列声学理论知识中,帮助国内关注声学应用的工程师,科研人员,高校老师,企业管理者等学习了解声学。各位读者看到的如下系列声学知识连载,是对于2015年出版的声学理论书籍法语版《Phénomènes fondamentaux de l’acoustique linéaire》(《线性声学基本现象》)的中文翻译。
续前节:《线性声学基本现象》Chapter 14 - 声在耗散介质中的传播
14.3
Biot理论
Biot【3】理论为声场中多孔材料的研究提供了一个通用的框架。

图14. 1:Maurice A. Biot (1905-1985)
各项异性的介质被等效为各项同性介质,各项同性介质由固体相(骨架)与流体相(一般是其中填充空气)组成; 骨架的体积含量为 (1 - Ω),空气的体积含量为Ω;
介质中任一点均具有一应力张量和声学压强;
声波的波长远大于材料的特征尺度(孔与纤维的直径,骨架的特征尺度);
骨架的位移属于小位移,使用线弹性假设;
大多数的孔为开孔;
封闭的孔被认为是骨架的一部分,封闭孔内流体的运动效应被忽略;
不存在背景平均流场,流体相没有宏观运动。
骨架的弹性参数: 杨氏模量 E;
泊松比 υ;
形成骨架的介质密度ρs
流体相的声学参数: 流体密度 ρf
流体的体积模量Q (简化的假设,可以使用 ,在14.3.7章中会有更详细讨论)
描述流体相与固体相间相互关系与作用的多孔介质参数: 孔隙率 Porosity: Ω
流阻 Resistivity: R
比奥因子 Biot Factor: α
孔道曲折度 Tortuosity:α∞
下面的章节会介绍Ω,R,α∞ 的物理意义与测试方法。比奥因子α在由空气饱和填充的多孔介质中总近似于1,这在14.3.4章节中会再做讨论。
孔隙率 Porosity: Ω
假设一个多孔介质的总体积为Vt,等于流体相体积Vf与固体相体积之和Vs 。则孔隙率Ω被定义为:
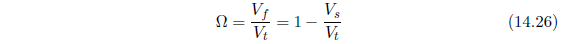
通过将一个体积为Ve的多孔介质样品置入到空腔体积为Vc的钢柱中可以测得孔隙率(图14. 2)。密封含有多孔介质样品的钢柱空腔,然后用一微调装置改变钢柱空腔的体积。空腔体积减小V,则其内压力从p1升至p2。钢柱有足够大的壁厚和热惯性可以保证该升压过程是个等温过程。假设忽略多孔介质固体骨架的可压缩性,则有:
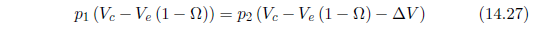
由此可得实测的孔隙率:
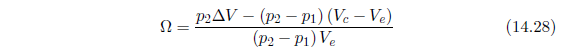

图14. 2:孔隙率测量装置.
流阻 Resistivity: R
空气通过多孔介质的流动受到流体相和固体相之间粘性相互作用的限制。粘性力同流体和骨架之间的相对速度成正比,如下:
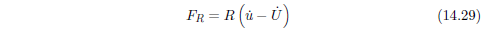
其中,R是多孔介质的流阻。静态流阻的测量方法是(图14. 4和图14. 5):将一厚度为h的多孔介质样品置于一个横截面为S的测试腔中,并使得空气流动(q =Sv)。用一差压计监测腔内样品上下游两侧的压力降p。此时流阻可以表示为:
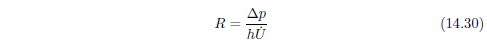
然而,样品的多孔性会减小其内空气通过时的有效横截面积,故在被测试样品内的空气流速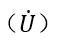 会大于测试腔内的流速(v)。
会大于测试腔内的流速(v)。
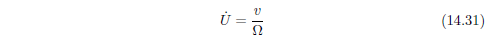
流阻的最终实验表达式为:
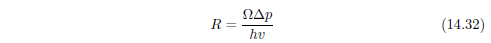
流阻R的单位为N.s/m4 或者 Rayls/m (Rayls是为了纪念Rayls勋爵【4】而引入的单位,)。而动态流阻取决于频率(将于14.3.7节描述)。

图14. 3:John William Strutt, third Lord Rayleigh
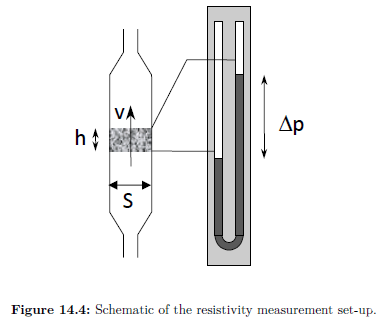
图14. 4:流阻测量装置原理示意图

图14. 5:流阻测量装置
孔道曲折度 Tortuosity:α∞
孔道曲折度表征了空气粒子在多孔介质中运动轨迹的复杂性。比奥将孔道曲折度定义为无粘流体微观分子速度的动能与宏观波动能的比值。孔道曲折度可以用电测法或超声法测得。
在电测法中(图14. 6和图14. 8),将多孔介质样品置于横截面为S的充满导电液体的柱体当中。样品在柱体中的位置可由两个坐标x2 ,x3来定义。样品上下两侧的电极产生一个大小为I的电流。测量位置x4和x5 之间的电势差V1,以及位置x1和x4之间的电势差V2。一般x4非常靠近于x3,而x2非常靠近于x1。如果我们假设多孔介质样品的孔隙被电解液充满,则这些电势差可以表示为流体的流阻和样品流阻的函数:
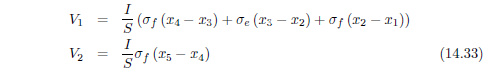
由上式可得:
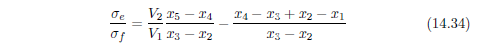
于是孔道曲折度的定义式如下:
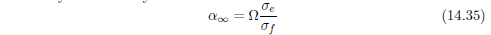
由于超声波脉冲通过多孔介质的传播速度取决于介质的孔道曲折度,故超声法更为简单精确。其测量装置由一个超声波发生器和接收器组成(图14. 7)。比较超声波脉冲在有无样品置入时的从发生器到接收器的传播时间差,可以推得样品的孔道曲折度。
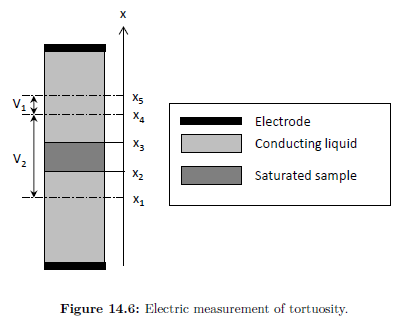
图14. 6:孔道曲折度的电测法原理示意图

图14. 7:孔道曲折度测量装置:超声法

图14. 8:孔道曲折度测量装置—电测法
【3】Maurice Anthony Biot,毛里斯 ·安东尼· 比奥, 美国比利时裔工程师(图14. 1),1905年生于比利时安特卫普,1985年在纽约去世。比奥发表了一系列关于多孔弹性体和饱和多孔介质力学的先驱性文章。今天,比奥理论被广泛应用在声学与土壤力学领域。
【4】John William Strutt,约翰·威廉·斯特拉特,瑞利男爵三世(图14. 3),于1842年11月12日出生,1919年6月30日去世。他在声音、波、颜色感知、电动力学、电磁学、光衍射、流体力学和流体动力学、气蚀、粘性、毛细管现象、弹性和摄影等领域都有贡献。





