后处理 Abaqus 的计算结果

 过冷水诚挚邀请你加入Matlab仿真秀官方交流群进行Matlab学习、问题咨询、 Matlab相关资料下载，qq：927550334 

   前面两章介绍了用 MATLAB 进行简单力学计算的方法，对于更复杂的力学问题，一般需要用功能更强大的商业化有限元软件，如 Ansys、Abaqus 等来完成。但很多时候，研究中还需对商业化软件计算结果进行进一步的分析，这就需要读取这些软件的计算结果并做后处理。 

    本章以 Abaqus 为例，简单介绍用 MATLAB 后处理其计算结果的操作方法。其他商业有限元软件的处理方法类似。 

12.1  商业有限元软件结果后处理的必要性 

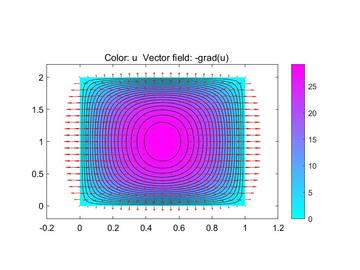
    随着计算技术、计算硬件的发展以及越来越多的需求，商业有限元软件的功能也越来越强大，不但计算和分析功能强大，其数据后处理功能也越来越强大。目前的商业有限元软件中，对计算结果可以进行统计分析，也可以进行各种形式的可视化（图 12-1） 。 

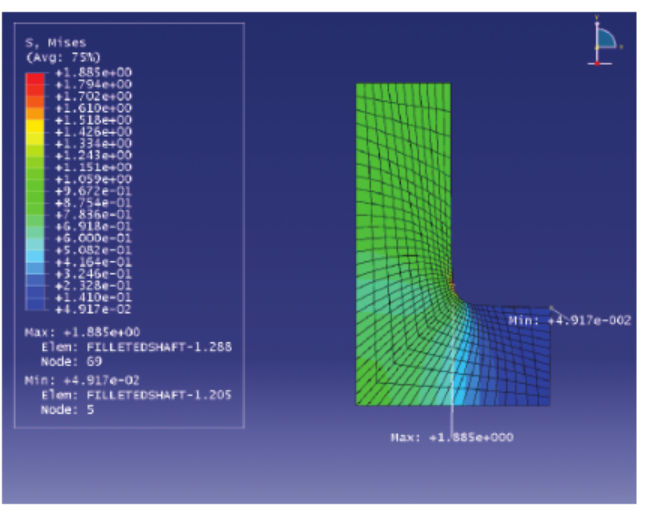
图 12-1  Abaqus 中显示的应力计算结果 

    但是，在实际应用中，这些现成的分析和可视化功能并不总能满足用户的要求。例如下面的几个例子。 

    ① 画一个计算结果与实验或解析结果的对比图。将计算结果与实验或解析结果相对比，是研究或工程中经常要进行的工作，但仅用商业有限元软件的后处理功能是不能完成这一工作的。因为有限元软件不提供将实验或理论结果导入后绘图的功能。更为重要的是，有限元数据结果中的数据点（节点或单元数据点）与实验观测的数据点很有可能是不对应的，也无法做比较。要完成上面的工作，需要将有限元计算结果导出来，然后用其他数据处理软件完成操作。 

    ② 对计算结果进行深入分析或从中拟合关系等。即使不和实验或解析结果对比，仅用计算结果分析，有时软件提供的功能也是不够用的。例如，对一个结构的应力场中的一部分进行“增强” ，使其更加突出。这需要先判定，划定区域，再进行分块操作。对于这种复杂的操作，商业有限元软件一般是不提供的。再如，从不同载荷的计算结果中拟合出一个关系式，直接用有限元软件完成这种操作也比较困难。 

    ③ 画一个符合发表规范的图。即使上面两个工作都不做，有限元软件的计算结果也直接就可以用，商业软件画的图在很多时候也是不能用的。如图 12-1 就不符合绝大多数期刊的绘图要求。 综上可知，将商业有限元软件的计算结果导出，然后用功能更强大、使用更灵活的语言（如 MATLAB）编程进行处理是很有必要的。 

12.2  Abaqus 计算结果的后处理 

12.2.1  问题描述 

    以一个对径受压圆盘应力分布的计算为例。设有一直径为 50 mm，厚度为 5 mm 的圆盘，受一对集中力作用（图 12-2） 。圆盘由环氧树脂制成， 其弹性模量为2.3 GPa， 泊松比为0.4。  用 Abaqus 计算其应力分布， 将中轴线上的应力与理论结果对比，将圆盘的最大剪应力分布与光弹性实验的等差线进行对比。  

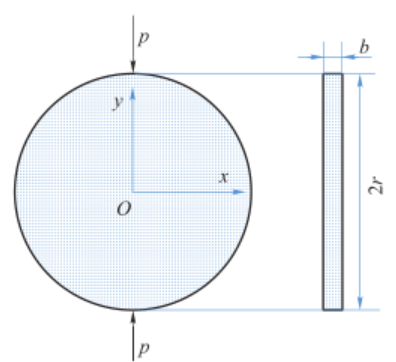
12.2.2  操作过程 图 12-2  对径受压圆盘示意图 

12.2.2  操作过程 

（1） 计算 

    用 Abaqus 建立有限元模型，如图 12-3（a）所示，施加载荷并设定边界条件后进行计算，得到的结果如图 12-3（b）所示。 

图 12-3  有限元模型及应力结果云图 

（2） Abaqus 数据的导出 

    从 ABAQUS 中可以导出两个存贮计算数据的文件： .inp 和.rpt 文件。 其中 inp文件中存贮了计算模型的几何数据，如节点的坐标和单元的节点信息等；rpt 文件贮存了位移、应力等计算结果信息。ABAQUS 的计算结果存贮在二进制的 odb 件中，用 report 选项可从 odb 文件中输出 ASCII 码的 rpt 文件。 

    inp 文件格式如下： 

*Heading
** Job name: brazilian_disc Model name: Model-1
** Generated by: Abaqus/CAE 6.10-1
*Preprint, echo=NO, model=NO, history=NO, contact=NO
**
** PARTS
**
*Part, name=Part-1
*Node
1, 0., 0.0219999999
2, 0., 0.0189999994
3, 0., 0.0170000009
…
*Element, type=CPS8
1, 246, 247, 328, 1048, 1206, 1207, 1208, 1209
2, 48, 437, 492, 504, 1210, 1211, 1212, 1213
3, 614, 52, 1066, 1091, 1214, 1215, 1216, 1217
…
*Nset, nset=_PickedSet2, internal, generate
1, 3549, 1
…

    在 inp 文件中，关键字“*Node”后面是节点的坐标信息，关键字“*Element”后面是单元的节点信息。后面还有其他关键字和其对应的数据信息。 

    rpt 文件格式如下。

…
Field Output reported at nodes for part: PART-1-1
Computation algorithm: EXTRAPOLATE_COMPUTE_AVERAGE
Averaged at nodes
Averaging regions: ODB_REGIONS

Node S.S11 S.S22 S.S12
Label @Loc 1 @Loc 1 @Loc 1
-----------------------------------------------------------------
1 3.72978E 06 -28.9362E 06 610.036E 03
2 1.91421E 06 -14.9593E 06 28.3204E 03
3 1.84509E 06 -11.4225E 06 8.96470E 03
…
Minimum -168.543E 06 -297.155E 06 -158.33E 06
At Node 19 19 19
…

    rpt 文件中第 23 行至倒数第 11 行的内容记录了节点与计算结果（位移、应力或应变等信息） 。 

    将上面两个文件对应起来，就可以得到空间坐标与计算结果的对应关系，从而可以生成计算结果的矩阵。 

（3） 后处理 ABAQUS 计算结果的具体过程 

    以前面巴西圆盘计算结果的后处理为例，设 Abaqus 输出的两个文件为brazilian_disc.inp 和 brazilian_disc.rpt。 

    首先读取“brazilian_disc.inp”文件中单元的节点的坐标，将其赋值给变量 x和 y。需要注意的是，由于 inp 文件同时包含了注释等说明信息，数据读取时需要先 通 过 查 找 关 键 字 的 方 式 确 定 数 据 的 位 置 ， 再 进 行 读 取 。 然 后 读 取“brazilan_disc.rpt”文件中的结果数据，将其赋值给变量 sigma_data。同样地，需要先确定数据的位置，再进行读取和进一步处理。读取数据后，x, y, sigma_data矩阵中分别存贮了节点的坐标和应力，有了这些矩阵，就可以用 MATLAB 完成本节中描述的问题了。 

    圆盘中轴线上应力的理论解与有限元解对比结果如图 12-4 所示。 

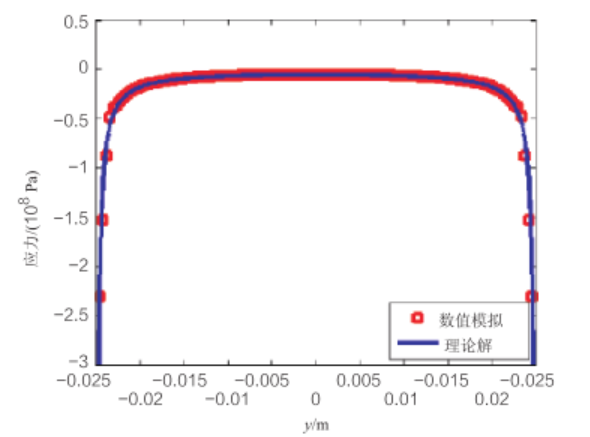
图 12-4  圆盘中轴线上应力的理论解与有限元解对比图  

句法 

    [A,B,C,...] = textread('filename','format') 

说明 

    textread 函数可以从文本文件中读取数据，其中 filename 就是文件名，format 就是要读取的格式。 

%==================================================================%
%% Curve.m
%% 本程序用于实现生成轴线上应力的理论解与有限元解对比图
%==================================================================%
close all
clear all
clc
%% 材料常数
d = 0.05; %圆盘直径
r = d/2; %圆盘半径
t = 0.005; %圆盘厚度
load = 700; %载荷
%% 计算理论应力场
xx = linspace(-r,r,255);
yy = linspace(-r,r,255);
[x,y] = meshgrid(xx,yy);%建立方形区域
circle = x.*x   y.*y - r.*r;%利用 circle 判别圆域
circle(circle>0) = nan;
circle(circle<=0) = 0;
ppi = 2/pi;
ydx = (y r).*(y r)   x.*x;
ydx = ydx.*ydx;
dxy = (r-y).*(r-y)   x.*x;
dxy = dxy.*dxy;
yd = (y r);
dy = (r-y);
sigma_x_th = (load*(- ppi * (yd.*x.*x./ydx   dy.*x.*x./dxy)   ppi/d))/t 
circle;
sigma_y_th = (load*(- ppi * (yd.^3./ydx   dy.^3./dxy)   ppi/d))/t circle;
%% 读取坐标数据
file_inp = textread('brazilian_disc.inp','%s','delimiter','\n');
%将 inp 文件以换行为分隔符读取成字符串
n1 = strmatch('*Node', file_inp); %查找数据开始的位置
n2 = strmatch('*Element,', file_inp); %查找数据结束的位置
node_data = str2num(char(file_inp(n1 1:n2-1)));
%将关键字之间的顶点数据转化为矩阵
x = node_data(:,2); %提取所有点的 x 坐标
y = node_data(:,3); %提取所有点的 y 坐标
%% 读取计算结果数据
file_rpt = textread('brazilian_disc.rpt','%s','delimiter','\n');
%将 rpt 文件以换行为分隔符读取成字符串
n3 = 23; %设定数据开始的位置
n4 = length(file_rpt)-11; %设定数据结束的位置
sigma_data = str2num(char(file_rpt(n3:n4)));
%将关键字之间的结果数据转化为矩阵
sigma_x = sigma_data(:,2); %提取所有点的 y 方向应力结果
sigma_y = sigma_data(:,3);
%% 绘制对比图
[x1,y1] = meshgrid(linspace(0,0.025,128),linspace(-0.025,0.025,255));
%设定插值区域
sigma_x_grid = griddata(x,y,sigma_x,x1,y1); %对计算结果插值
plot(y1(:,1),sigma_x_grid(:,1),'LineWidth',3,'Color',[1 0 0],...
'DisplayName','数值模拟'); %绘制中轴线上数值计算结果曲线
hold on
yy=linspace(-r,r,255); %生成中轴线上结果的坐标空间
sigma_x_midline=sigma_x_th(2:length(yy)-1,128); %截取中轴线上理论解结果
plot(yy(2:length(yy)-1),sigma_x_midline,'LineWidth',3,...
'DisplayName','理论解'); %绘制中轴线上理论解结果曲线
legend1 = legend('show'); %添加图例
set(legend1,'Location','SouthEast','FontSize',15);
%设置图例位置及字体大小
ylabel('Stress(Pa)'); %设置 x 轴名称
xlabel('y(m)'); %设置 y 轴名称
ylim([-1.6e8 0.3e8]);

    光弹性实验中的等差线代表了光弹性材料（如环氧树脂）制成的模型中的最大剪应力分布，图 12-5（a）所示为与本计算模型中同尺寸光弹模型实验中的等差线。为验证计算结果，可将同样载荷下的有限元计算结果与实验中的等差线绘制在一起，如图 12-5（b）所示。 

图 12-5  等差线比较 

（a）光弹实验等差线条纹； （b）实验等差线与有限元计算结果对比 

%==================================================================%
%% BrazilianDisc.m
%% 本程序用于实现显示实验中的等差线与有限元计算结果的对比图
%==================================================================%
close all
clear all
clc
%% 读取节点坐标数据
file_inp = textread('brazilian_disc.inp','%s','delimiter','\n');
n1 = strmatch('*Node', file_inp);
n2 = strmatch('*Element,', file_inp);
node_data = str2num(char(file_inp(n1 1:n2-1)));
x = node_data(:,2);
y = node_data(:,3);
%% 读取计算结果数据
file_rpt = textread('brazilian_disc.rpt','%s','delimiter','\n');
n3 = 23;
n4 = length(file_rpt)-11;
sigma_data = str2num(char(file_rpt(n3:n4)));
[x1,y1] = meshgrid(linspace(-0.025,0.025,256),linspace(-0.025,0.025,
256));
sigma_x = griddata(x,y,sigma_data(:,2),x1,y1);
sigma_y = griddata(x,y,sigma_data(:,3),x1,y1);
sigma_xy = griddata(x,y,sigma_data(:,4),x1,y1);
%% 计算最大剪应力
sigma1 = (sigma_x sigma_y)/2 1/2*sqrt((sigma_x-sigma_y).*(sigma_x- sigma_y) …
4*sigma_xy.*sigma_xy);
sigma2 = (sigma_x sigma_y)/2-1/2*sqrt((sigma_x-sigma_y).*(sigma_x- sigma_y) …
4*sigma_xy.*sigma_xy);
sigma_xy_max = (sigma1-sigma2)/2;
%% 绘制对比图
I=sin(sigma_xy_max/0.203e6);
imshow(I,[min(I(:)) max(I(:))])
hold on
left = imread('left.bmp');
imshow(left);

        过冷水发表于 仿真秀 平台原创文章，未经授权禁止私自转载，如需转载请需要和作者沟通表明授权声明，未授权文章皆视为侵权行为，必将追责。如果您希望加入Matlab仿真秀官方交流群进行Matlab学习、问题咨询、 Matlab相关资料下载均可加群：927550334。

精品回顾

 matlab绘制农夫过河动态图

分子动力学的原子空间运动轨迹演示编程

过冷水带你用matlab制作演示动画

python批量移动文件&重命名代码分享

过冷水和你分享 matlab读取存储各种文件的方法 文末有独家金曲分享