编写一个简单的有限元程序

过冷水诚挚邀请你加入Matlab仿真秀官方交流群进行Matlab学习、问题咨询、 Matlab相关资料下载,qq:927550334
![]()
本章以一个简单的弹性力学问题——求解受均布载荷作用悬臂梁的应力分布为例,简单说明如何应用MATLAB编写有限元程序,完成力学计算分析。
10.1 用有限元求解问题的思路和步骤
10.1.1 总体思路
弹性力学的微分方程(组)是建立在一个连续的求解域上的,用有限元求解问题时,需要将求解域离散为有限个部分(图10-1)进行求解:离散后的每个小部分称为单元; 每个单元由若干个节点连接而成;节点的位移构成单元的自由度;单元内的变形由节点位移通过一些假定的基函数来表达,这些基函数称为单元的形函数。

图 10-1 连续体离散过程示意图
根据有限元的理论,模型离散化后,以所有节点的位移为未知量,用能量最小原理最终可将离散模型问题转化为求解一个线性方程组:
Ke=F (10-1)
式中,K为有限元模型的总刚度矩阵;F为节点载荷向量;e为节点位移向量,是需要从方程中求解的。在求解出e后,可进一步得出应变和应力等。
10.1.2 求解步骤
以一个简单的弹性力学问题为例进行说明求解步骤。 如图10-2所示平面悬臂梁模型,左端为固定端,上部受均布载荷q作用。求解x方向的正应力。

图 10-2 悬臂梁模型
有限元的具体实施过程如下。
(1) 单元划分
将模型划分为若干个单元。本例中选用平面四节点矩形单元,将模型划分为四个单元,并给单元和节点编号,如图10-3所示。

图 10-3 有限元模型
(a)单元划分; (b)直角坐标系下单元示意; (c)正则坐标系下单元示意
平面四节点矩形单元的每个节点有两个自由度,因此该模型共有20个自由度。位移向量e和节点载荷向量F的维度为20×1,总刚度矩阵K的维度为20×20。
(2) 确定位移向量和节点载荷向量
根据物理模型写出位移向量e和节点载荷向量F。对于本例,可知节点位移向量为
e=[e1 e2 … e20]T (10-2)
由于节点1和6固定,可确定e1、e2、e11、e12为0,其他自由度未知,需要求解。
节点载荷向量为
F=[p1 p2 … p20]T (10-3)
其中,p1、p2、p11、p12未知,剩余的分量中,p20=aq,p14=p16=p18=2aq,其他为0。
(3) 求解单元刚度矩阵ke
平面四节点矩形单元有4个节点,8个自由度,因此ke的维度为8×8。根据有限元理论可知

其中

其中

为单元的局部坐标;

为节点i在局部坐标系的坐标值。
对于平面应力问题

对于本例中的平面4节点单元,最终ke可表示为

其中kij是2×2的矩阵,具体形式为 
(4) 组装总体刚度矩阵K
根据有限元理论,刚度矩阵中的元素表示当节点发生单位位移时引起的节点力。在单刚ke中,kij表示j节点发生单位位移且其他节点位移为零时,单元在i节点引起的节点力。类似地,在总刚K中,Kij表示j节点发生单位位移且其他节点位移为零时,整体结构在i节点引起的节点力。由于结构已经被离散为若干个单元,该节点力为所有与i、j节点相关的单元在i节点引起的节点力之和。因此,总刚是由单刚按一定规则组装起来的。
根据有限元总刚组装规则,对前述问题的总刚进行计算。
已知总刚度矩阵K的维度是20×20,将其分成10×10的分块矩阵,每个分块矩阵为2×2,下面所有的操作均为对分块矩阵的操作。
首先组装单元1,此时的总刚度矩阵所有元素均为0。单元1的刚度矩阵为k1。单元1中四个节点依次对应整体模型的编号是1、2、7、6(按逆时针顺序) 。将k1中分块矩阵的下标1、2、3、4依次用1、2、7、6代替,并叠加到K矩阵的对应标号的分块矩阵上。单元1组装完成后,再对单元2进行组装。前两个单元组装完成后的K如图10-4所示。

图 10-4 组装了两步的总刚
依次对所有单元完成组装,得到的K如图10-5所示。

图 10-5 总刚 K
(5) 求解方程
组装完成后的K不是一个满秩矩阵,若不做处理,方程(10-1)没有唯一解。因此,在求解之前,需要将已知边界条件引入,以使K满秩。对于本问题,具体做法是:将K矩阵的第1、2、9、10行和列去掉,同时将e、F向量的第1、2、9、10行去掉,组成一个新的线性方程组

进行求解。线性方程组求解可用数值分析中的各种算法完成。
(6) 后处理
后处理主要包括求应力、应变以及画图显示结果等。记任一单元8个自由度的位移向量为δe,则单元内任意一点的应变为

单元内任意一点的应力为

10.2 用 MATLAB 编写简单有限元程序
10.2.1 流程
根据上一节介绍的有限元的思路和步骤,可设计用Mablab编制有限程序的步骤如图10-6所示。具体实现过程为:首先输入模型参数,包括材料参数、外载荷,以及各单元的节点坐标及其在整体模型中的编号;然后依次计算各单元的单刚矩阵,并组合到总刚矩阵里;最后进行求解。

图 10-6 有限元程序的编写流程
10.2.2 算例实现
已知有一受均布载荷的悬臂梁,给定参数:l=8 m,h=2 m,b=0.2 m,E=3 GPa,μ=0.3,q= -1KN/m。编写有限元程序对问题进行分析。
(1) 程序
先针对简单问题进行编程。假设将模型划分为4个单元。程序为:
%==================================================================% %% 文件名:FEM4element.m %% 功能:实现四边形单元计算受均布载荷悬臂梁 %% 用到子函数 cal_K_e()和 cal_K() %==================================================================% clc clear all %% material parameters E = 3E9; %弹性模量 nu = 0.3; %泊松比 b = 0.2; %梁厚 q = 1000; %均布载荷的大小 n_no = 10; %节点个数 Ne = 4; %单元个数 ele = [1 2 7 6; 2 3 8 7; 3 4 9 8; 4 5 10 9]; %每个单元的节点编号 x = [0 2 4 6 8 0 2 4 6 8]'; %每个节点的 x 坐标 y = [0 0 0 0 0 2 2 2 2 2]'; %每个节点的 y 坐标 %% load F0 = zeros(2*n_no,1); F0([14 16 18]) = 2000; F0(20) = 1000; F0([1 2 11 12]) = nan; index = find(~isnan(F0)); %% displacment e0 = zeros(2*n_no,1); e0(index) = nan; K = zeros(2*n_no,2*n_no); for i = 1:Ne k = cal_K_e(b,x(ele(i,:)),y(ele(i,:)), E, nu);%% 单刚 K = K cal_K(n_no, ele(i,:), k); %% 总刚 end %% 求解 e0(index) = K(index,index)\F0(index); F = K*e0; D1 = E/(1-nu*nu)*[1 nu 0; nu 1 0; 0 0 (1-nu)/2]; B = 1/4*[-1 0 1 0 1 0 -1 0; 0 -1 0 -1 0 1 0 1; -1 -1 -1 1 1 1 1 -1]; %% stress strain strain = B*e0([ele(:,1)*2-1 ele(:,1)*2 ele(:,2)*2-1 ele(:,2)*2 ... ele(:,3)*2-1 ele(:,3)*2 ele(:,4)*2-1 ele(:,4)*2])'; stress = D1*B*e0([ele(:,1)*2-1 ele(:,1)*2 ele(:,2)*2-1 ele(:,2)*2 ... ele(:,3)*2-1 ele(:,3)*2 ele(:,4)*2-1 ele(:,4)*2])'; %==================================================================% %% 文件名:cal_K_e.m %% 功能: 计算单个单元的刚度矩阵 %==================================================================% function k = cal_K_e(h,x,y, E, nu) k = zeros(8,8); a = (x(2)-x(1))/2; b = (y(3)-y(1))/2; l_x = [-1 1 1 -1]; l_y = [-1 -1 1 1]; for i = 1:4 for j = 1:4 k(2*i-1:2*i,2*j-1:2*j) = [b/a*(1 1/3*l_y(i)*l_y(j))*l_x(i)* l_x(j) ... a/b*(1-nu)/2*(1 l_x(i)*l_x(j)/3)*l_y(i)*l_y(j),nu*l_x(i)*l_y(j)... (1-nu)/2*l_y(i)*l_x(j);nu*l_y(i)*l_x(j) (1-nu)/2*l_x(i)*l_y(j),... a/b*(1 1/3*l_x(i)*l_x(j))*l_y(i)*l_y(j) ... b/a*(1-nu)/2*(1 l_y(i)*l_y(j)/3)*l_x(i)*l_x(j)]; end end k = h*E/(4*(1-nu^2))*k; end %==================================================================% %% 文件名:cal_K.m %% 功能:实现各个单元刚度矩阵的组装 %==================================================================% % function K = cal_K(n_no,ele,k) K = zeros(2*n_no,2*n_no); DOF = [2*ele(1)-1:2*ele(1), 2*ele(2)-1:2*ele(2), 2*ele(3)-1:2*ele(3), 2*ele(4)-1:2*ele(4)]; for n1 = 1:8 for n2 = 1:8 K(DOF(n1),DOF(n2)) = K(DOF(n1),DOF(n2)) k(n1,n2); end end end %%
其中cal_K_e()为计算单刚的函数,计算结果如下。

cal_K( ) 计算总刚的函数,计算结果如下。

最终计算获得的位移和节点载荷结果如下。


获得位移向量e0后,可以计算获得单元的应力、应变,结果如下。
(2) 结果分析
根据弹性力学知识,悬臂梁的应力解为

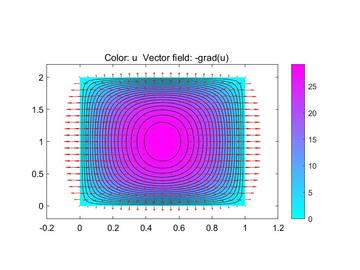
与解析解相比,前述程序的计算结果显得很粗糙,这是因为计算中采用的单元太少, 对问题离散得不够。 将有限元模型中的单元进一步细化, 使单元达到1 600个(单元大小为0.1 m×0.1 m) 。用新的程序计算,所得数值解比较光滑,也更接近于解析解,如图10-7所示。

图 10-7 受均布载荷悬臂梁 σx应力
(a)有限元解; (b)理论解

过冷水发表于 仿真秀 平台原创文章,未经授权禁止私自转载,如需转载请需要和作者沟通表明授权声明,未授权文章皆视为侵权行为,必将追责。如果您希望加入Matlab仿真秀官方交流群进行Matlab学习、问题咨询、 Matlab相关资料下载均可加群:927550334。
精品回顾
过冷水和你分享 matlab读取存储各种文件的方法 文末有独家金曲分享