热测试（一）——ETM法测量结温

电子产品热设计总体包括两大重要环节，热仿真和热测试。热仿真是应用CFD软件对被测目标（芯片，PCB，系统，超系统）进行模拟，从而预测被测目标的温度分布。

热测试——通过各种手段，推算或者测量芯片的结温。因为结温是热设计上限，控制结温是热设计非常重要的目标。传统测量结温的方法一般都是通过测量壳温，再根据θ_jc推算出结温。

T_j = T_c  θ_jc*P

     T_j  ：    结温

   T_c  ：  壳温

     θ_jc：  结壳热阻

     P   ：    功率

这个公式的原形是热欧姆定律

θ_jc =△T/P=（T_j-T_c）/P

△T=（T_j-T_c） ：结到壳的温度梯度

该公式脱胎于电欧姆定律R=U/I 电阻=电压/电流。热阻对应于电阻，温度梯度对应于电压的压降，电流对应于功率。

这说明热传导相对于电传导有一定的可比性。电的绝缘体的电阻率大概是10¹⁰欧姆·米，而常温下，电的良导体铜的电阻率是0.0172(µΩ• m)，两者相差接近20个数量级；反观常温下热的绝缘体空气的热导率大概是0.026W/（m·K），热的良导体铜的热导率大概是385 W/（m·K），两者相差仅仅5个数量级。这就说明热的传导，不可能像电传导那种一维传导路径，而是一种三维空间的传播方式，因此我们在使用热欧姆定律时，必须要考虑一些限制条件。

下图是功率元件三维热分布的示意图。

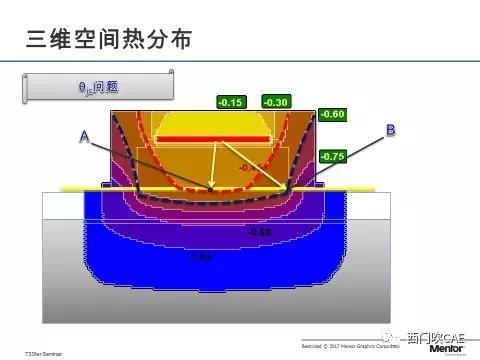
图一 功率元件的三维空间热分布

上图黄线上半部分是芯片（功率元件），下半部分是热沉，通过任何一个仿真软件抽取出的等温面（二维图即是等温线，如果上图所示），可以看出，在热沉和芯片之间的接触面上（黄线所示），其温度是按照中间高周围低这样一个规律分布的，最高的显然是A点，第一个到达热沉的等温面。按照结壳热阻的定义θ_jc=（T_j-T_A）/ P，我们只有准确的测出A点温度，再根据准确的 θ_jc推算出结温。然而实际应用上A点温度很难测量（有一种方式是在热沉上钻一个洞，这种方式测出来的也未必觉得准确），工业上通常用测量最近的管脚B点的温度来替代A点的温度，而上图可以清楚的看出，B点的温度显然要比A点的温度要低几个温度梯度，这样推算出来的结温要比实际结温低，如果用这个结温作为设计的目标，系统的安全性就得不到到保障，为了弥补这个问题，不同生产厂商，他们的datasheet里面 θ_jc都存在一定的冗余量（Margin）来防止设计时对结温的过低评估， 但是冗余量在业界并没有标准化。

实际上壳温的测量也非常困难，工业上常用测量壳温的工具是热电偶和红外摄像仪，不同的大小的热电偶，不同贴热电偶的方式，不同使用的人，都会带来不同的误差。而红外摄像仪测量温度需要设置热辐射率，这个热辐射率只能设置一个值，测量温度分布是没有问题，温度的精度就难以保证了。

也就是说，按照datasheet里面 θjc，结合测量的壳温推算出来的结温比实际结温要高，而高多少，并不知道。

有没有办法能够准确知道结温呢，当然是有的，用ETM（电气法），如下图：

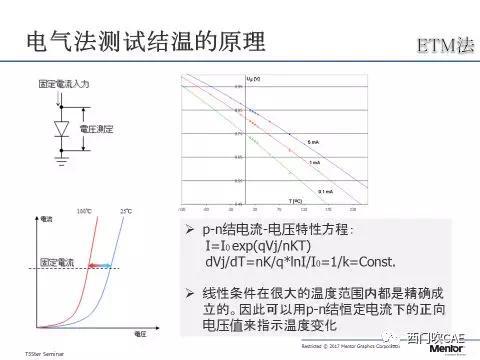
图二 ETM法

根据结电流-电压特性方程，在一定的电流下，可以看出结温和结电压成负线性相关，也就是说，如果知道该元件线性相关的斜率K，只要用测试电流（该测试电流很小，不会引起器件发热）测出结电压，就可以知道结温。用这种方式测量结温的精度，取决于电压测试的分辨率，其重复性非常高，如果电压的分辨率可以保证的情况下，精确度也可以非常高。

K系数的测量方法也很简单，通过一个控温设备（冷板，恒温箱等）去控制环境温度，给被测器件通上测试电流（该电流不会引起器件发热），把被测器件放置在控温设备中，通过改变环境温度，会得到不同的结电压，连线后，很容易得到该器件在该测试电流下的K系数。

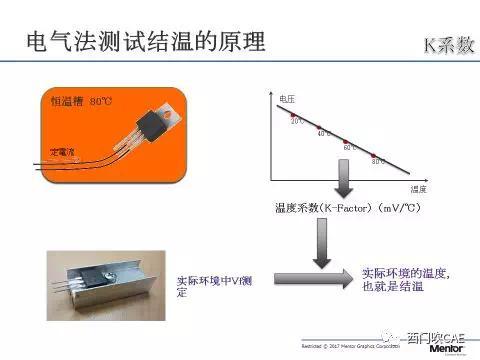
图三 K系数的测量

到目前为止，我们具备了瞬态热测试的基本条件，在后面的章节，我们会介绍静态法瞬态热测试技术，以及探讨结构函数在电子设备热设计中的具体应用。

未完待续