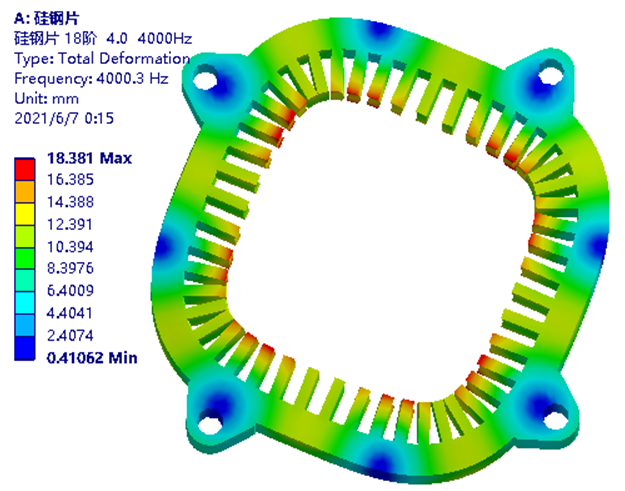
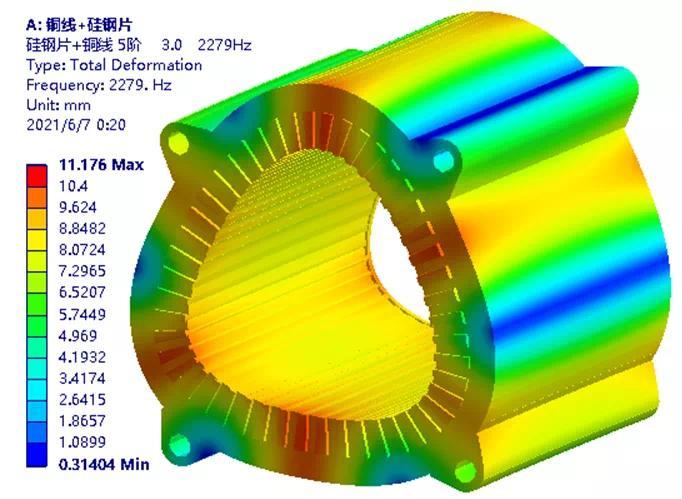
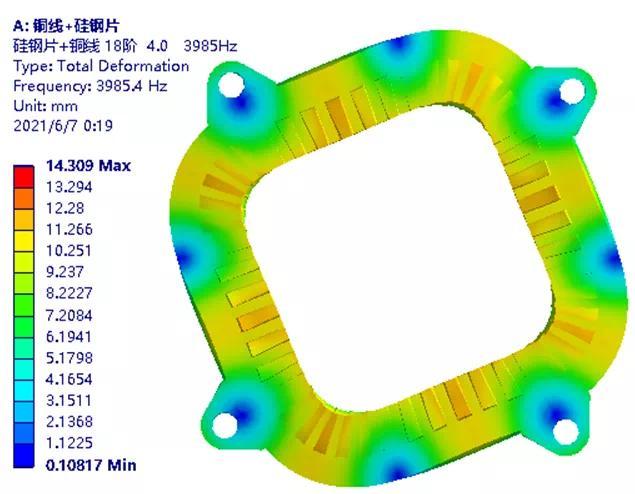
误差仅1%!油冷电驱动系统电机定子弹性模量的验证方法
本文摘要(由AI生成):
文章主要介绍了电机定子自由模态仿真分析方法,包括几何建模与清理、网格划分、材料属性对标等。其中,几何建模与清理对精度影响较大,网格划分原则包括删除几何模型细节特征并圆润化,材料属性对标包括硅钢片与铜线的弹性模量等。文章还介绍了自动优化方法,通过遗传优化算法进行筛选优化,最终将定子模态仿真的前6个主要特征阶次模态频率与自由锤击模态实验结果对应的最大差异控制到1.5%左右,平均差异0.5%左右。
一、写在前面
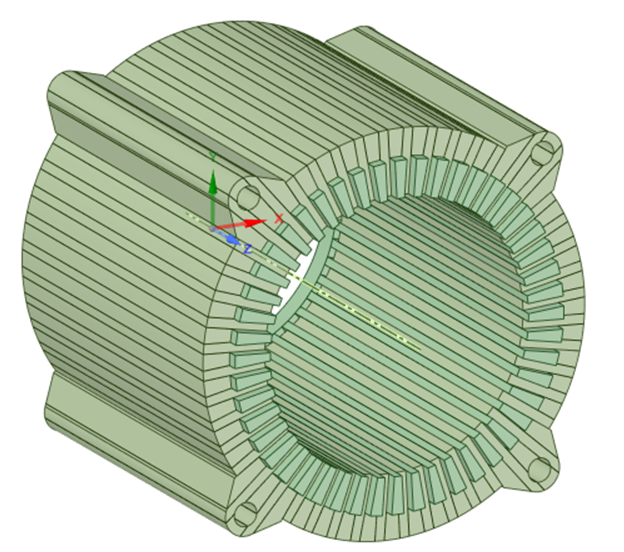
拥有符合自由敲击模态实验的高质量的电机定子自由模态仿真结果,是后续整机模态、振动、噪音等NVH相关计算精度与性能实现的重要基础性工作。本文以新款日产尼德科品牌,介绍峰值功率为150KW油冷电驱动系统的定子模型为例,进行模态、网格及等效弹性模量等参数的验证仿真分析方法。

本案例所用模型,对应产品型号为Ni150Ex,如下图。相传,李德胜大大在《矛盾论》有云:“事物的性质,主要由取得支配地位的,矛盾的主要方面确定。”对于电机定子模态仿真而言,影响计算精度的各因素,由以下几个方面构成:第一、几何建模与几何清理精度,其对精度影响比例约±20%;
第二、网格形式与密度分布,其对精度影响比例约±50%;
第三、符合实际的材料属性,其对精度影响比例约±50%;
第四、外部支撑与固定的刚度,其对精度影响比例约±100%等。
则仿真精度的上下极限误差范围,约1.2x1.5x1.5x2=±540%。而较高质量的计算结果,一般可控制到正负10%甚至5%左右。采用本案例方式,可进一步优化至1%上下。也就是说,所谓高手和水手间的差距,可拉开约100倍。但两者薪资待遇的差异,则远远小于与此。对于模态仿真而言,主要与刚度成正比且与质量反比。前者主要受到弹性模量、支撑刚度、网格数量与密度等影响。后者主要为模型的形状、尺寸、密度等影响。影响计算精度的主要矛盾为,材料属性中的等效弹性模量以及网格划分方式的选定。二、仿真前的准备工作
开始仿真分析前,首先简单介绍一些模态仿真与试验的背景信息。1、线性假设。即无法考虑摩擦、碰撞、塑性变形等非线性部分。同时频率响应函数,不会随着外部激励而发生变化。当采用自由锤击法,进行模态实验时,可采用不同大小的锤击力进行敲击,并查看频响函数的一致性,从而判断结构是否满足线性假设。否则,频率响应函数如果随着激励变化,而发生频率移动,则认定本结构,将存在一定的非线性成分。2、时不变假设。即结构特性不会随着时间而改变。则实验时可多次重复实验,而可保证结果不变。但对于PCBA等轻量材料,为尽量避免实验时,移动加速度传感器前后,对整体模态的影响,应尽量将加速度传感器,均匀分散到PCBA各处。同时,温度等外部环境变化,也将影响弹性模量及内应力等分布,则实验时应保证各条件的横向一致。3、可探测性假设。即所有数据和特性,都是可以被探测到的。但是也应注意实验时,应尽量采用不同锤击与加速度传感器的粘贴位置,以试图激发出全部模态信息。对于特定阵型方向的模态,激励的方向也尽量与之接近,从而更好的进行激发和测量。根据采样定理,传感器采样频率,为关注频率的二倍以上,否则易于混淆。最后,传感器的布置,应尽量避开各主要模态的节点处。其可通过多次实验并移动加速度传感器的固定位置,进行对比验证。4、互异性假设。即在A处敲击测量到结果为B,如果换过来,在B处敲击测量的结果也是A。基于此,其可通过多次移动传感器固定位置,进行对比验证。采用自由锤击法实验,也是为了尽量避免,因外部固定约束关系,对结构刚度产生的不易探测的影响,从而降低问题复杂度,使精度更为可控。相同的,模态仿真时也可不设置任何约束关系,仅计算自由模态,从而更利于进行试验对照。同时,根据被测件刚度的不同,应选用不同材质(弹性模量)组成的锤头。一般而言,锤头材料的弹性模量应稍大于被测件。如使用钢制锤头,轻轻敲击铝质电机壳体等。三、定子模态空间特性
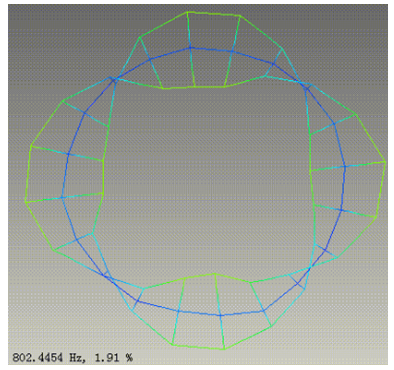
常规而言,传统的模态阶次顺序,按照模态频率,从小到大顺序排列,并对应其阵型。宏观而言,电机定子为圆柱体状,实际可采用更为简约的方式进行表达。其空间模态特性,可根据节点(振幅为零)位置及数量,采用mode(m,n)方式描述。其中m为圆周方向的节点数,n为轴向。一般对电机定子或机壳等,圆柱体类模型的仿真及实验时,周向模态考虑前5个,同时轴向模态,考虑1个节点,即可拥有足够的精度。如1.0、2.0、2.1、3.0、3.1、4.0、4.1、5.0、5.1等。如下图所示。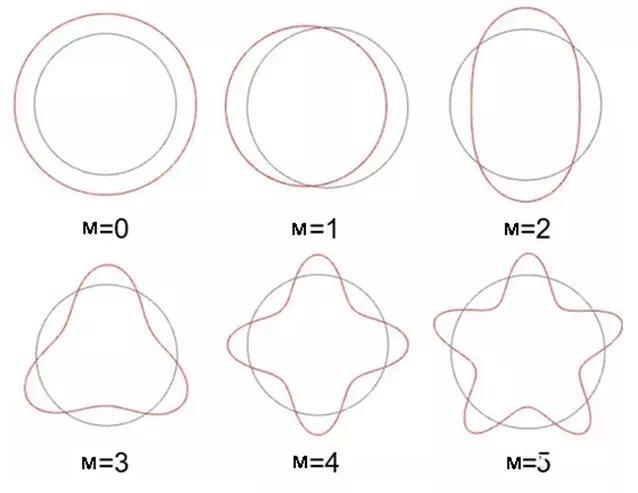
图3 定子周向模态特性
其中m=0为呼吸模态,即周向同步振动,类似呼吸状而得名。对于电机NVH问题而言,该模态有时为在机械侧,诱发噪音的主要矛盾。这就是为什么很多电机的机壳表面,设计大量径向环状加强筋的原因。但从全局角度审视,定子等效弹性模量,约为铝质机壳的2倍,同时电机直径尺寸,相对定子鄂部对铝质机壳厚度亦较大,则机壳加强筋带来的少量刚度变化,极易被以上两个因素所埋没。故如非必要,则可尽量减少机壳上,大量增加环状加强筋的设计思想。从而尽量降低总体重量、尺寸、成本等代价,提高材料利用率。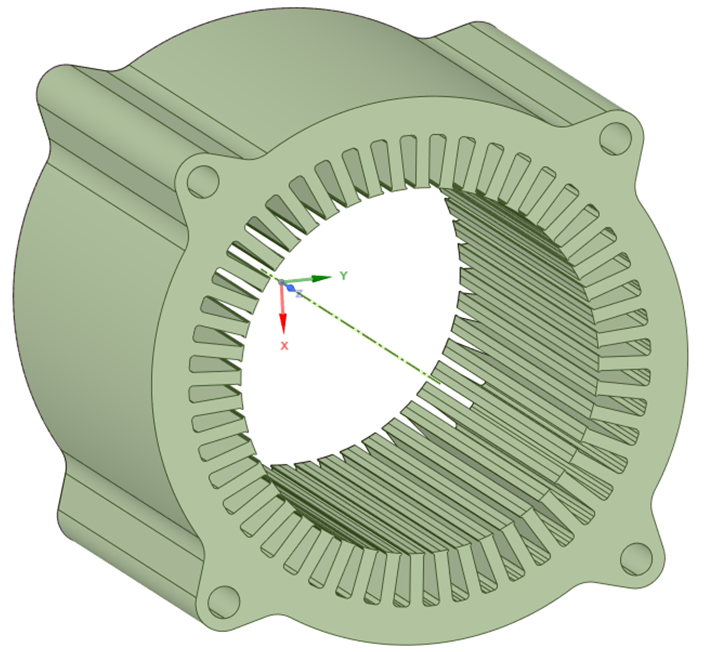
图-5 单独定子几何模型

四、网格划分原则概述
根据“抓大放小”的基本行为准则,参考汽车行业常用的D-FMEA编制思路,优先定位到网格的密度与数量、单元形状、单元插值函数阶次、网格质量等,是影响模态仿真分析中,离散误差范围的主要方面,同时也是后续网格相关验证工作的重点。对于本文案例,随着网格密度的变化(一般为每次网格尺寸,在上一次基础上减少30%~40%,并连续重复3~6次),各主要特征阶次,如2.0、2.1、3.0等关键模态阵型,对应的频率结果,趋于稳定且变化极小,则可认为该结果,实现了与网格的无关性,或者说完成了,计算结果的网格无关性验证。这是实现高精度模态仿真的必备过程。该过程为对硅钢片 铜线模型的方向性判断。故计算得到的模态阶次,为前10阶~20阶时,当基本得到了诸如2.0、2.1、3.0等,少数关键模态阵型结果即可,从而尽量降低网格验证阶段的计算成本。模态分析的主要计算结果,为总体变形类。则网格划分时,建议采用全局基本一致的网格尺寸与密度分布;而相反的,对于强度分析等应力类仿真,由于应力集中现象的存在,则需对局部关键区域,基于应力等值线的分布趋势,采用逐层渐细的网格尺寸分布,而远离处可逐渐粗糙(圣维南原理)的方法。从而平衡计算成本、难度、精度间的矛盾。同时,模态分析为基于有限元方法的数值模拟仿真技术。对于有限元应力类分析的基本流程,为节点位移、节点变形、单元应变、单元应力、总体应力。其越靠前而计算精度相对越高。从而在使用较为粗糙的网格尺寸与密度时,计算精度即可满足要求。总体应力结果,为计算的最后阶段方可得到。其经历了多重计算与数据转化过程,精度相对较低。故需采用非常细密的网格,方可将结果精度,控制到合理范围。同时,由于网格较为粗大时,结果中存在单元应力与总体应力的差异,故应力类仿真分析的网格无关性验证,在本文所述方法基础上,还需进击的增加一组,应力磨平前单元应力分布与磨平后总体应力分布结果差额的验证过程。一般而言该差异小于5%为合格。但达到此类要求,需要的网格数量较多。其综合计算成本,为变形类的5倍~10倍。从全局角度审视,一味追求网格对结果的影响,甚至一组工程计算,却追求“好看吗?好看就是好网格”的单方面网格精度崇拜和六面体网格崇拜,容易造成一叶障目、坐井观天、夜郎自大的盲目与偏执以及在混沌蹉跎间,造成的高成本。建议对所有影响计算精度的因素,挨个排查并验证,且根据影响程度与改善难度,分配相关精力与资源,力求将最影响精度的因素,进行重点排查及控制(2-8原则),方可实现符合木桶效应的总体精度与成本的有效控制。本文主要采用,不同网格尺寸及不同单元阶次的多次,定子模态仿真分析对比验证,从而筛选出达到结果的网格无关性,且成本最低的仿真方案。电机定子作为三维实体模型,可采用的网格单元形状,主要为四面体及六面体两种。采用四面体网格,对几何模型的复杂度及细节特征的容忍度较高,同时网格划分和控制非常简单,综合成本极低。缺点是网格数量相对六面体可能翻倍,以至于仿真时对内存的需求,可能超过计算机的内存容量,造成被动借助虚拟化技术,不得已使用速度极慢的硬盘进行数据存储容量补偿,以部分代替内存需求空间,继续进行仿真分析。其将使总体计算时间,增加10倍~100倍。极端时,由于内存容量严重无法满足要求,甚至无法进行计算;采用六面体网格,需保证模型的每一个局部,都满足可以“一键生成”的简单形状要求,如通过拉伸、扫描、放样等方式,建立的矩形、梯形、菱形等零件。这是因为六面体网格划分时,一般基于零件的一个侧面作为基准面并布局网格单元,而后沿着某一个方向,进行其他单元的平推和旋转等操作,从而将网格单元进行,逐步边拉伸边的方式,生成并填满整个实体零件。该方法与几何建模阶段的扫描与放样极为接近,故形状越接近此类一步建模的局部,也越容易被六面体网格生成。其需提前对几何模型,进行大量分割与剖分操作。从而将高度复杂的一个整体零件的模型,分批切割为大量形状简单的局部零件。同时,以上六面体网格划分思路,也意味着需对复杂模型,尽量删除细节倒角、碎面、凸台、凹陷等破坏“一键生成”原则的部分,并尽量将几何轮廓,简化并调整至圆润、平滑、饱满的基本特征。条件一:删除几何模型细节特征并圆润化;
- 条件二:对总体模型切分并组合为,多组可“一键生成”的局部零件。
其生成难度与成本,将相对四面体网格的简单易行又“不挑食”更高。故四面体网格方案,相对较为适合“只争朝夕”的企业工程计算,尤其是电驱动壳体模态分析这类,无需考虑细节模型特征的仿真项目。但对于本文案例而言,定子与铜线的形状较为简单,可通过不算复杂的一些剖分操作,生成全六面体网格,从而抵消了部分前处理成本。对于本文案例,定子模型共拥有48个定子齿槽,可对每一个齿槽的两侧,进行径向切分操作。从而将原设计的一个总体零件,切分为近百个,近似矩形的条状局部零件。并通过共享拓扑方式,将切分后的多组零件,组合为一个新的装配体,从而实现网格划分时,不同几何模型零件的交界面之间,网格节点的对应与共享。另一个推荐的几何模型切分思路为:由于定子分齿部与锷部两处。可首先对齿部外径一侧根部进行环形切分,而后对外圈锷部附近4组螺栓孔附近,再次径向切分的方式。否则需使用绑定或者tie接触等方式进行连接。但接大量接触的存在,将极大增加计算成本与计算机内存需求。如未进行合理的简化及分割切分,使几何模型中仍残留了,任意形状复杂的部分,其将无法以六面体网格方式划分,而不得不生成四面体网格。其相对四面体网格策略,可能多消耗5倍~10倍的工作量与难度,以至于综合成本巨大,且计算精度与四面体不相上下,综合性价比堪忧。优点是网格数量,相对四面体可能减半,从而降低计算机内存需求,并节约计算时间。因为六面体的网格分布,看起来更规整顺滑,对于非技术人员及强迫症患者的视觉冲击力与诱惑力更强。大部分情况下,非技术指引的强调六面体网格划分,将是基础操作者的悲剧。无论四面体或六面体网格,对于每个单元的内部,是否考虑了中间节点,又可细分为无中间节点(一阶)与有中间节点(二阶)两类。则交叉组合后,进行完整的网格无关验证操作时共需分别试进行:1、四面一阶(每个单元4个节点);2、四面体二阶(每个单元10个节点);3、六面体一阶(每个单元8个节点);4、六面体二阶(每个单元20个节点)等,四种可能性的对比计算。当不考虑其他因素时,仿真分析的计算量与内存需求量,基本与网格总体节点数量,成正比关系增长。经试算,用于本案例的定子及铜线模型,其总体网格尺寸划分,可分别采用6mm、4mm、3mm、2.5mm等四种,并基本满足上文介绍的,每次减少30%~40%并连续重复3~5次的基本思路。其与网格形状及是否考虑,一二阶次单元的四种情况交叉组合后,共需对4x4=16次重复计算中选最佳,即可得到符合网格无关验证,且计算成本最低的方案。对于本案例,首先对任意网格形式及尺寸划分网格后,复 制相关case并调整尺寸及网格划分方式即可。以上工作需重复16次,但可借助软件左上角的update功能,在完成全部仿真设置后,一次性顺序自动计算所有结果。
图-8 网格无关性验证用计算文件
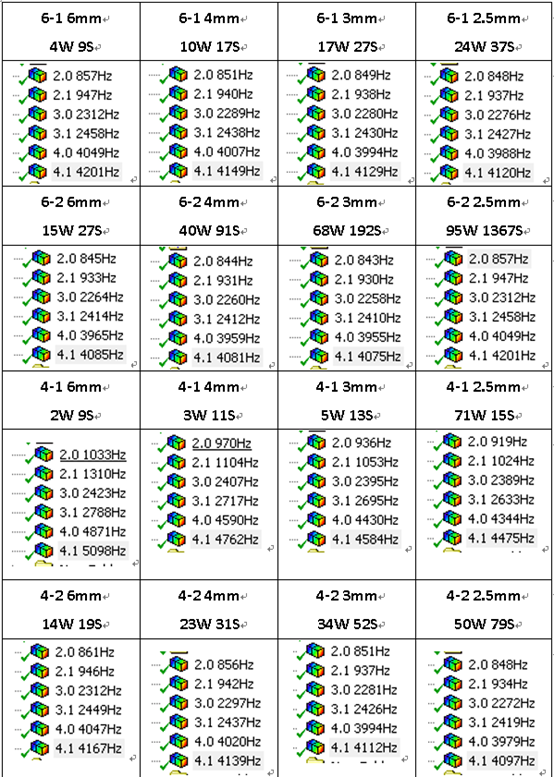
下面对本案例,所采用的不同网格形状及尺寸设置下,实际生成的网格分布情况,进行横向对比展示。下面为人工强制设定以四面体方式,机械划分的网格分布情况。一般而言,对于三维实体模型,推荐其沿着厚度方向,最少划分3层二阶单元或者4层一阶单元,可得到较高的结果精度。并注意单元质量,即远离标准四面体或六面体的差异程度,越小则网格精度越高。其中以上网格设置中,六面体一阶6mm时,约4万节点数、4mm约10万、3mm约17万、2.5mm约24万;六面体二阶6mm时约15万、4mm约40万、3mm约68万、2.5mm约95万;下表中分别为16次网格无关验证阶段中,单元形状、阶次、网格节点数量、求解时间、各关键特征模态频率、每次仿真计算时间等汇总。其中六面体一阶4mm总体网格尺寸时,其计算结果基本稳定,且求解时间极短(17秒),十分有利于后续大量参数化验证时,控制计算量。图-17 网格无关验证过程与结果横向一览表
通过对比以上结果,还可发现一个基本规律为,四面体一阶网格的模态频率,普遍高于其他10%及以上,则代表其刚度相对较高。如4mm网格尺寸时,四面体一阶的2.0模态为970Hz,其他为850Hz左右,其相对差异为15%。虽然对于大规模计算时,如果三合一整机的模态及扫频震动仿真,有时可能为降低内存需求,而不得不使用四面体一阶网格,但应时刻留意该10%左右精度的影响。五、材料属性对标概述
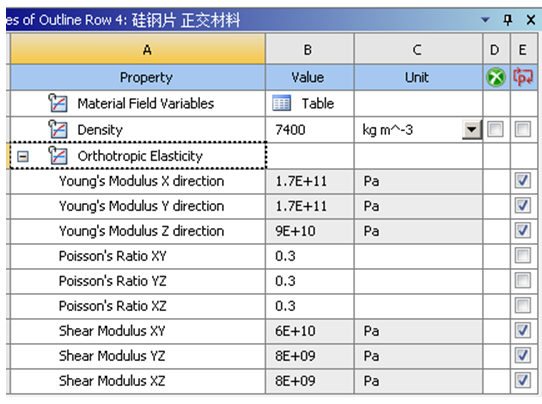
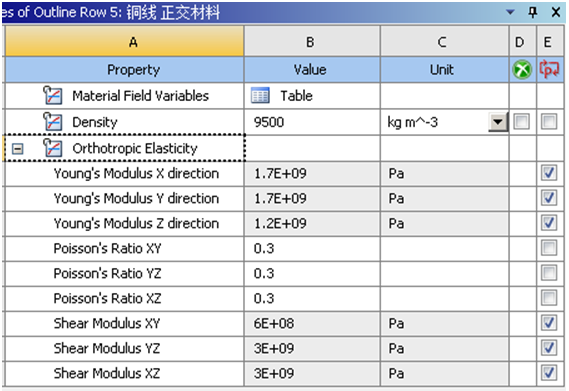
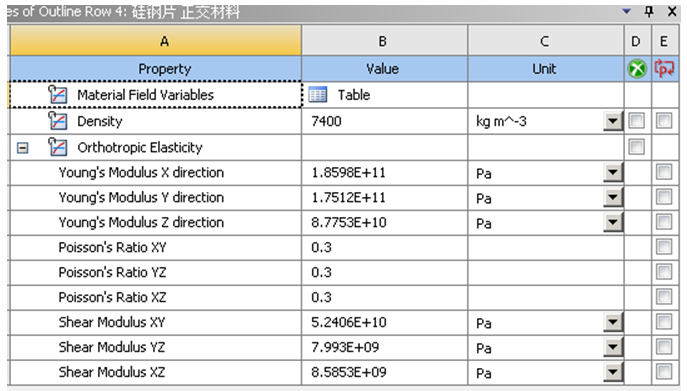
电机定子自由模态分析时,材料属性部分中,影响计算精度的主要参数为弹性模量,次要参数为密度与泊松比。其等效密度值,可将各零件分别称重获得。模态分析时的结构体积基本不变,可基本不考虑泊松比影响,故选用金属材料常用的0.3。电机定子主要由硅钢片与铜线,两种主要材料组成。次要材料为铜线表面绝缘漆、定子槽内绝缘纸、浸漆等。依赖“自下而上”工作法,对其进行等效弹性模量对标验证时,也应先校准单纯硅钢片,后进行硅钢片 铜线,共计最少两轮仿真验证过程。新能源汽车用驱动电机中,常用的硅钢片,一般为厚度0.2mm~0.35mm的冷轧薄片状带材,经冲压后通过粘接、榫铆、焊接、铆压等方式进行互相叠压固定;铜线为0.5mm~1.5mm圆形铜线或者4mm左右矩形扁铜线组成。待铜线下线完成后,经真空浸漆或滴漆等工艺,将铜线、绝缘纸、硅钢片等进行固定。由于下线后定子间,存在一定缝隙与间隙,而浸漆或滴漆后的渗透填充能力也存在一定差异,则不同工艺方法与参数间的定子浸漆质量存在分散性,将在一定程度上,影响定子总体的刚度表现,并影响铜线的等效弹性模量值。这使得无法通过简单估计方式,得到适合自由锤击模态实验的等效弹性模量。同时由于其不同方向刚度不一致,而采用传统计算验证方案中,只设置一个基于各项同性假设的弹性模量方法,将无法快速进行对标校准。建议先期对大量相同工艺方法与参数的多组浸漆后定子,进行自由锤击模态实验测试,方可发现规律,并尽量避免相关影响。同时,经大量对比累计后的模态数据,也可作为现场生产时,使用简单锤击并借助相关手机APP,快速验证浸漆质量的检验指标与方法。电机定子总成中,由于薄片状定子硅钢片 多根铜线 铆接及焊接等,细节结构及特征的存在。如完整精细建模,每一个细节特征,其计算成本与计算量将不可承受。则一定需要借助某种方式方法,进行几何模型与刚度表达的简化与等效。 对于硅钢片,其沿轧制的不同方向,拥有互相垂直关系的三种刚性,同时多片轴向叠压后,其不同垂直方向的刚度也有所区别。其不适用进行传统仿真分析,所采用的基本假设之一各项同性假设时,仅需设定一个弹性模量的方法。而需针对XYZ三个方向,采用正交各项异性弹性模量,共需6个模量的方法进行刚度等效。对于浸漆后的铜线,其轴向与径向的刚度,沿着正交关系有所不同,也需使用正交各向异性的6个弹性模量参数,方可表达其不同方向的刚度差异效果。图-19 铜线初始6个模量参数值
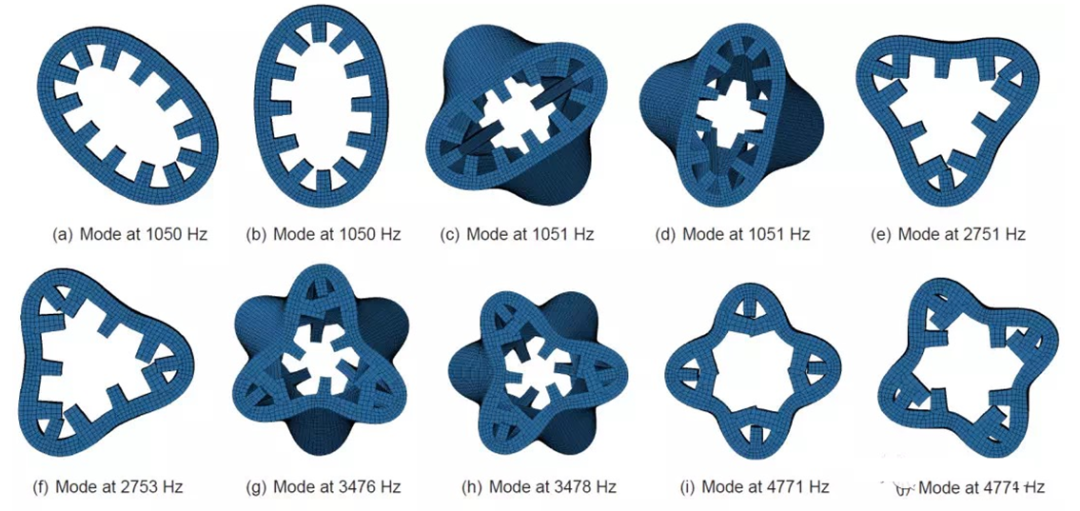
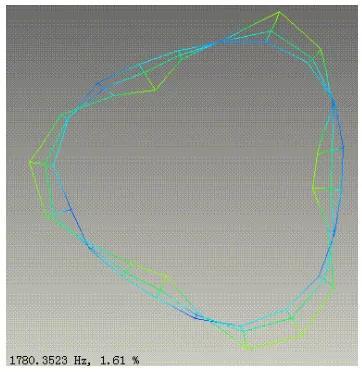
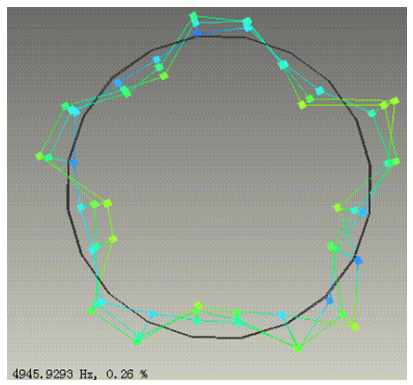
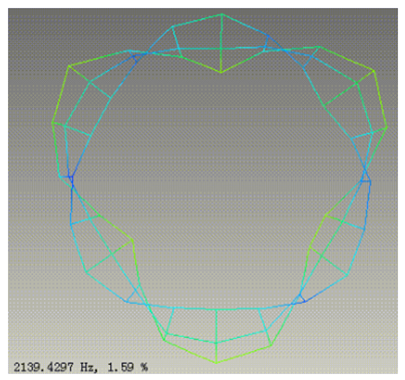
仿真前,可借助自由锤击模态实验方法,进行多组同批次同制造方法的,定子总成的重复试验,并找到2.0、2.1、3.0、3.1、4.0、4.1等,关键阶次模态特征结果的中位数,依此为目标函数,使用仿真软件中的参数化优化模块,并搭配模态分析模块,进行自动筛选。下面几组图片,为借助LMS等专用模态测试软硬件系统,得到的典型电机定子,关键特征阵型及频率值。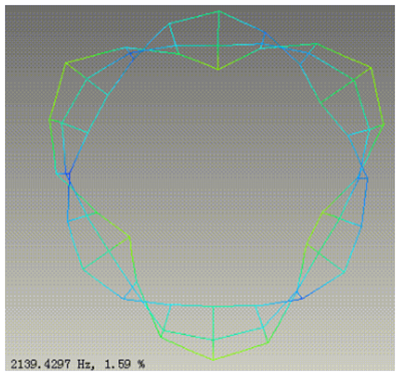
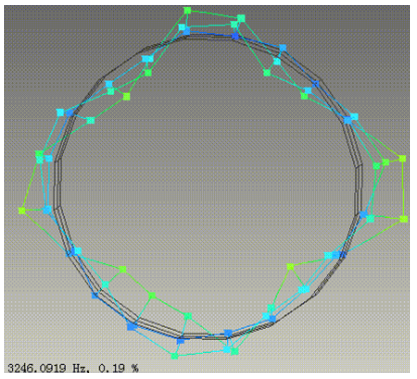
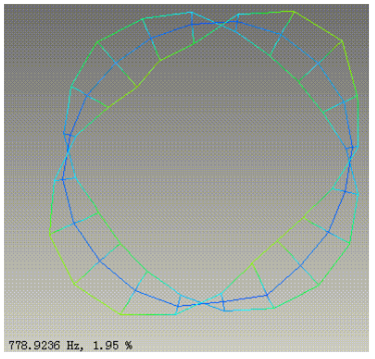
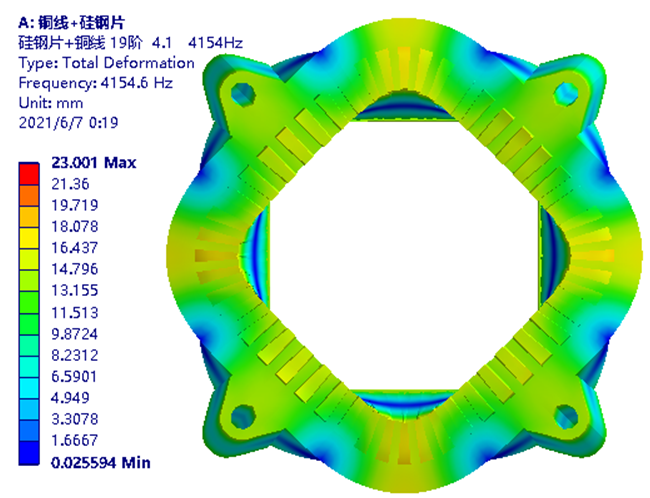
图-27 模态试验典型4.1阵型
六、材料属性的渐进式对标方法
自动优化方法。定子与铜线均为正交各项异性材料。为准确表达其刚度特征,共需12个弹性模量。交叉组合后,可产生成千上万种不同的组合方式。如依次借助手工试算方法,即使采纳正交实验表等技术的帮助,其工作量与成本也不可接受。但借助仿真计算软件及优化模块的自动参数化筛选方案赋能后,将相对手工试算的效率与质量,提升一到两个数量级,即实现所谓的降维打击。一般而言,依靠纯手工试算方法,验证等效弹性模量,需耗时4星期~6星期,并且非工作时间,一般无法连续产出成果。精度可达到与模态实验,各主要阶次频率的差异平均为5%~10%。进一步的,使用优化模块搭配模态仿真方法,进行自动筛选仅需约1星期,且与实验的相对差异,可提升到1%甚至0.5%,并可7x24小时连续进行,可极大的提升工作效率与计算精度。下面为本案例仿真分析用,计算机软硬件配置。其中央处理器,为测试版志强牌铂金系列的8272。
具体操作时,可采用基于多组典型的,自由锤击模态实验的对标验证数据为基础,而后模态仿真分析时,先单件后整机的渐进式理念,逐步深入对标验证的工作方法进行。基本分析思路是,首先对叠压后的定子,进行等效弹性模量的验证。而后以最符合实验的6个弹性模量数据为基础,在定子模型基础上,添加铜线模型,再次对下线及浸漆后定子,进行自由锤击模态实验结果与模态仿真校准即可。细节操作方法为,对多组叠压后硅钢片及浸漆后定子,进行称重记录。使用实验模态测试软硬件,对定子模型的基础轮廓进行。将加速度传感器,贴至定子外表面,采用固定传感器-移动击锤方法,在验证了结果符合互易性、线性、时不变等假设后,分别轻轻锤击实验测试建模时,设定的多组基准点。模态实验注意事项。试验时注意不要连击,同时将锤击后的相干性曲线,尽量清爽平顺的结果进行保存。加速度传感器,尽量粘贴至定子的轴向两端附近,从而尽量避免关键模态的振动节点处,对测试精度的影响。击锤的敲击点,尽量远离关键模态的节点位置。对于本案例,关注的最高阶4.1模态阵型的频率约6KHz。则试验时加速度传感器的最高探测频率,可选择12.8KHz及以上。同时根据采样定理,采样频率最低为其二倍,即25.6KHz及以上。模态实验精度满足要求后,汇总不同锤击点数据,进行后处理并借助肉眼判断,如2.0、3.0、4.0等关键特征模态阶次与频率结果,而后进行模态仿真分析。
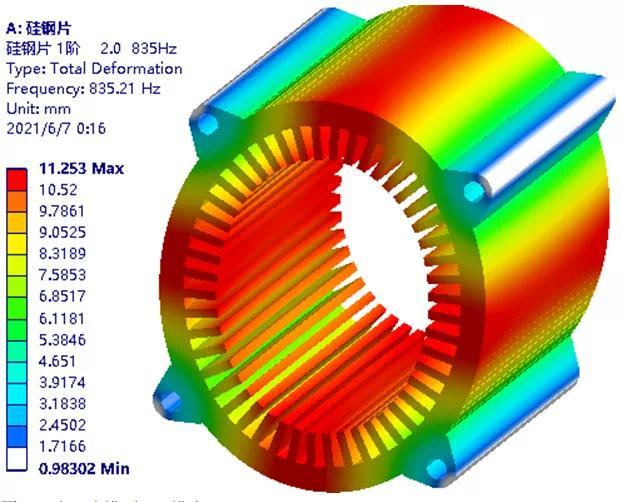
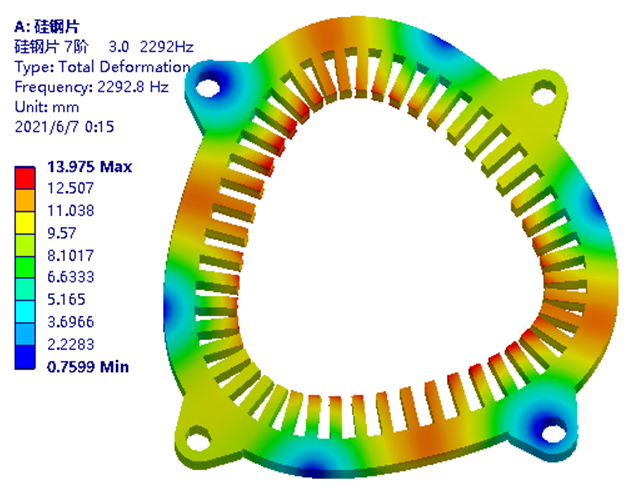
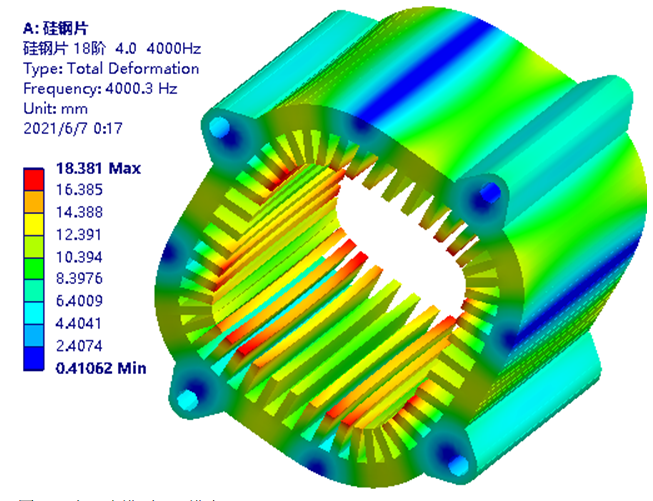
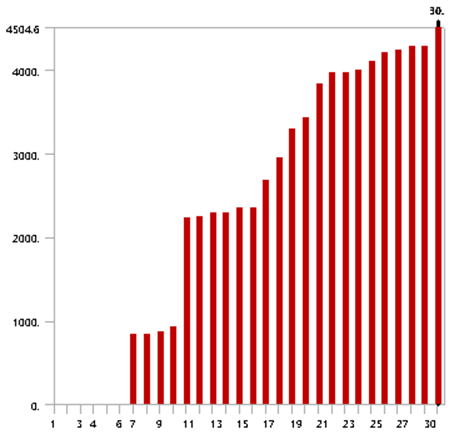
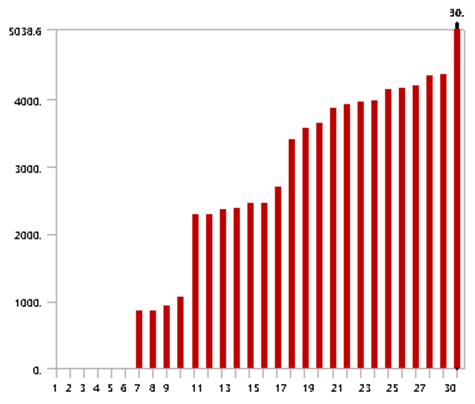
下面计算提取前30阶,模态频率的直方图表示。注意;由于自由模态前6阶,为刚体模态阵型,则真实1阶模态结果,从第7阶开始计数。
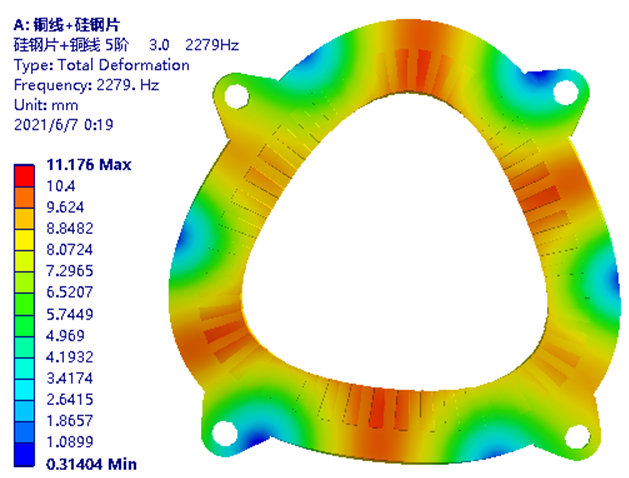
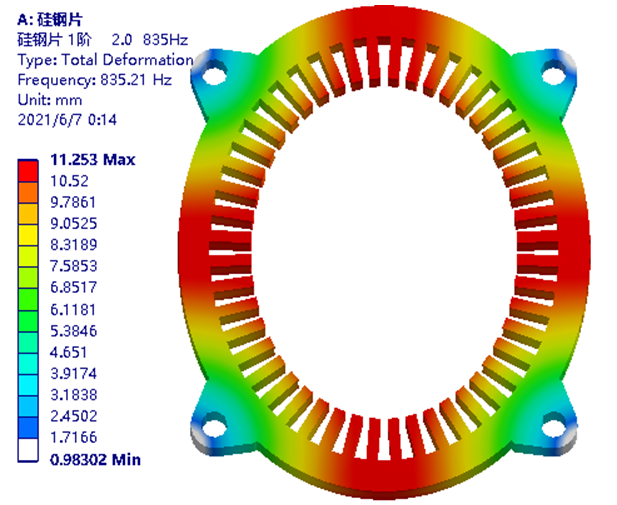
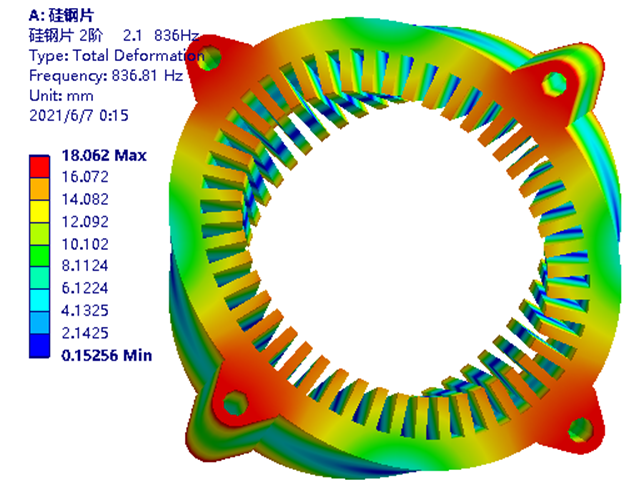
图-46 硅钢片加铜线模型前30阶模态频率分布情况仿真时,根据称重结果,分别设定硅钢片与铜线的等效密度值。而后分别设定6组正交弹性模量。可根据以往经验,先期大致输入XYZ方向弹性模量以及XY、XZ、YZ方向剪切模量数据与泊松比。采用上文经网格无关性验证的建模及网格划分方式,计算前30阶~80阶模态结果。并根据试算结果判断,达到最高可体现4.1阶模态结果时,最少应计算的模态阶次,从而降低计算成本。而后以模态仿真得到的2.0、2.1、3.0、3.1、4.0、4.1等,关键模态阵型对应的频率(也需肉眼判断,存在一定误差),作为参数化优化模块的目标函数,并设定其与模态实验中,对应阶次模态频率相同。为方便横向对比,不同自由锤击模态实验,关键阶次阵型与仿真的异同点。下面采用两个并列汇总图,以方便查看。图-48 仿真与实验模态阵型对应关系1
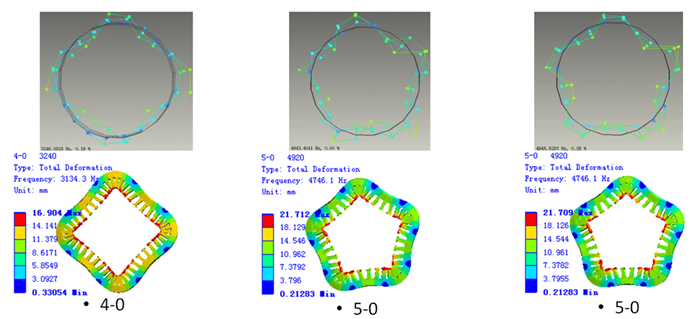
模态仿真后,提取各阶模态阵型与频率结果。通过以此肉眼观察30阶结果中,最符合2.0、2.1等关键模态阵型及其频率结果,将其结果单独命名,并在详细信息最下方的频率结果的前方,单击生成蓝紫色“P(英文参数化的首字母)”字样显示。即可用于后续优化模块时,以该模态阵型的频率,为优化目标之一而用。
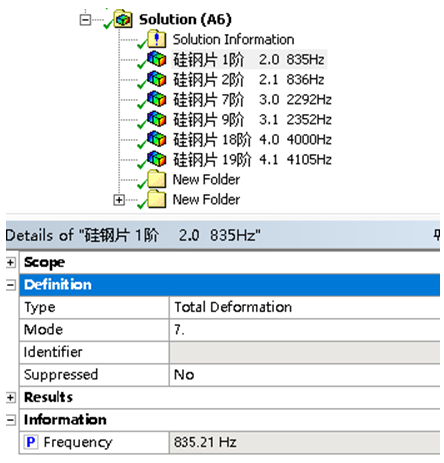
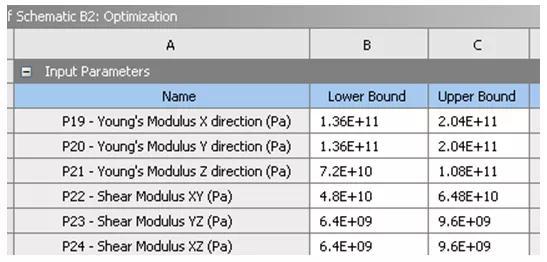
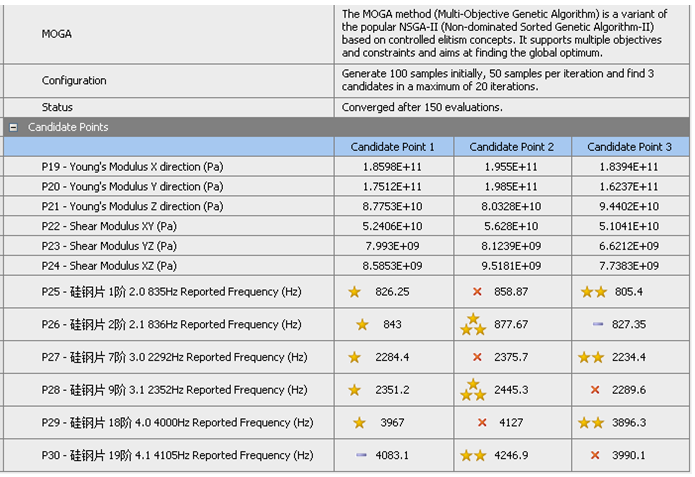
以硅钢片的6个弹性模量为设计变量,并设定每一个模量±20%左右的上下限范围。常用的优化算法为筛选法、单目标优化、多目标优化、遗传、蚁群等。推荐采用遗传优化算法,进行自动筛选优化。并根据每一轮约150个材料组合样本中,尽量符合试验模态频率,最后在前3名结果中选最佳。
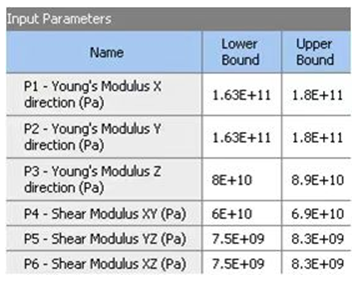
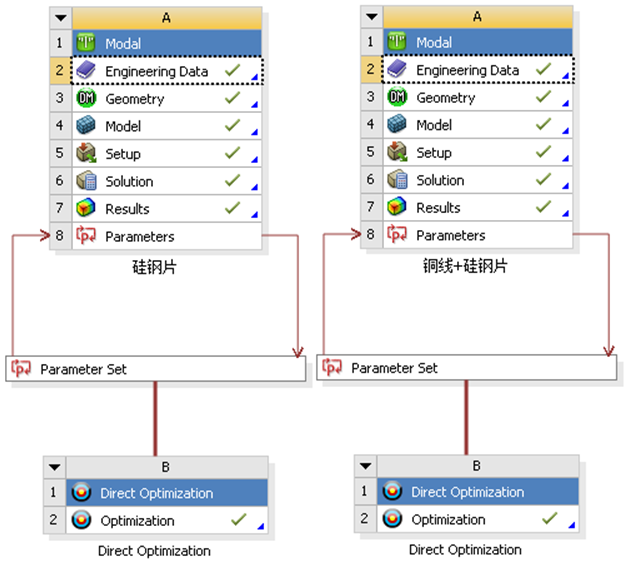
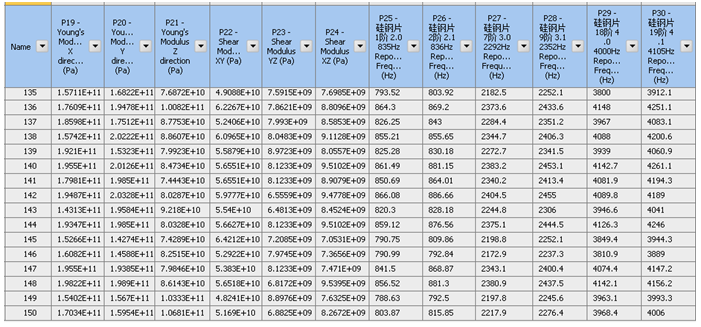
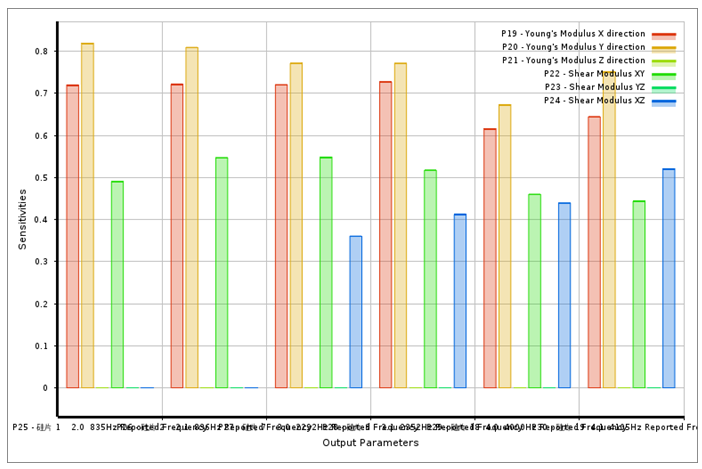
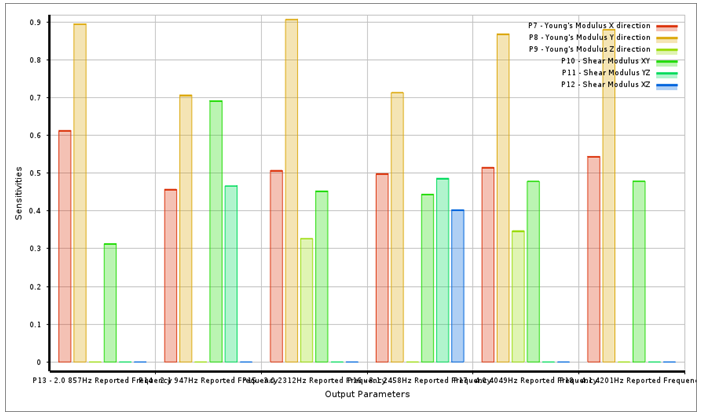
假定第一轮测试中,对硅钢片自由锤击模态实验,得到的前几阶,关键特征模态频率的中位数,为793Hz(2.0)、877Hz(2.1)、2711Hz(3.0)、2469Hz(3.1)、3800Hz(4.0)、4310Hz(4.1)。可以此设置为第一轮,硅钢片等效弹性模量验证的目标函数。为方便试算,可采用较大筛选范围的弹性模量值。当结果区域稳定时,可考虑进一步采用更小更窄的筛选范围,从而降低计算成本。进行多次优化迭代分析后,可提取下图所示的,6个模量分别对结果的敏感度。其数值越大于零,则其模量的贡献影响越明显,也越正相关。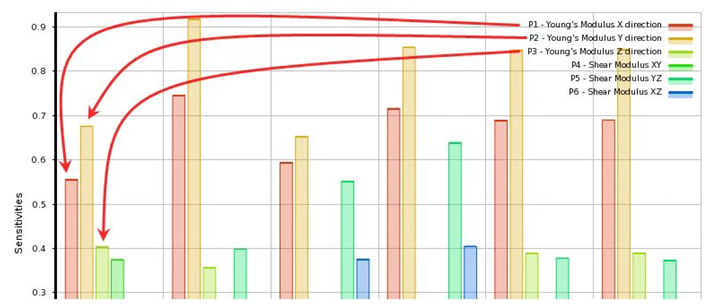
对于本文案例,遗传优化算法的核心思想,主要参考生物进化时,基本遵循的“物竞天择,适者生存”的基本原理,通过一组粗选的弹性模量组合数据,组建一个基本种群,后分别计算其,关键模态特征的频率结果,并分别与自由锤击法模态实验中,得到的对应阶次的频率的目标函数值进行比较。试图从中寻找到,相对更符合实验的几组优先数据。并依此为第二代弹性模量优化时的初选种群,使其互相“交配”并孕育出第三代子孙,以扩大种群数量,再次进行对比试算。经反复多轮,从而试图逐渐得到,在子子孙孙的后代种群中,优中选优的结果。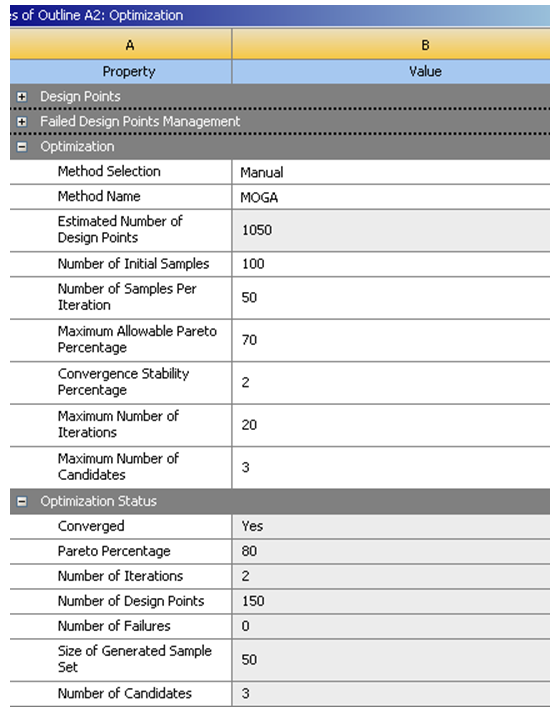
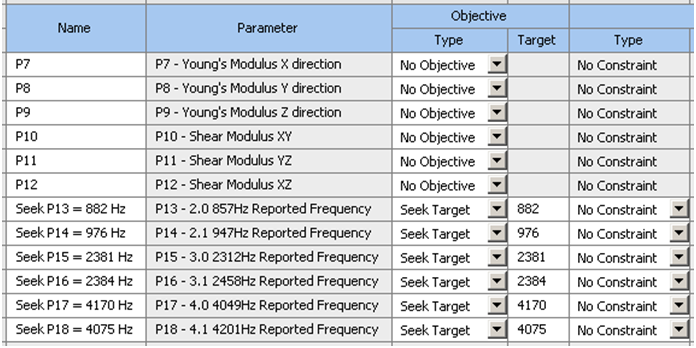
优化模块运行时,可随时监控不同弹性模量变量下,已完成的不同阶次模态频率结果的分布情况。优化完成后,可查看不同参数随着试算进程的深入,其筛选及变化过程的细节。经多组数据筛选,软件自动选中,相对最符合目标函数的,弹性模量组合前三名。虽然计算机经过150种不同弹性模量组合试算后,虽然已经得到前三位,最符合目标函数的弹性模量组合结果。但不同结果的相对误差可能仍然较大。此时需依靠肉眼判断,并权衡利弊。对于本案例,选取最左侧结果为准,并将其带入下一轮,新增铜线材料的验证仿真之中。以下敏感度直方图中,Z方向杨氏模量以及YZ方向剪切模量的敏感度几乎为零,说明其不影响计算结果。至此,在第一阶段仿真中,硅钢片符合模态实验的6组等效弹性模量已知。而后将铜线模型,添加入硅钢片中,并将铜线与定子齿槽交界面处,借助CAD软件中的使用组合功能,以将二者的网格节点,进行共享与连接。而后使用上一轮验证后的硅钢片弹性模量,设置为硅钢片材料属性中。其他的铜线部分,同样采用正交各向异性弹性模量,先估算6个模量值,后采用与上文相同方法,得到铜线 绝缘漆 绝缘纸 浸漆等综合部分的等效弹性模量。本轮仿真由于已经通过上一轮弹性模量的验证,获得硅钢片材料的6组等效弹性模量,则可直接修改材料属性,但删除其设计变量资格,并将铜线的材料属性,作为新一轮模态仿真的设计变量值,假定第二轮硅钢片加铜线自由锤击模态实验中,各关键特征阶次的频率分别为:882Hz(2.0)、976Hz(2.1)、2381Hz(3.0)、2384Hz(3.1)、4075Hz(4.0)、4170Hz(4.1)等。图-62 第二轮优化中设计变量与目标函数设置
至此,经4种单元形式、4种总体网格尺寸共计16次网格无关系验证计算,以及2轮共计398次试算,得到的12个符合实验的,等效弹性模量结果的对比验证,可将定子模态仿真的前6个主要特征阶次模态频率,与自由锤击模态实验结果,对应的最大差异控制到1.5%左右,平均差异0.5%左右的极高质量。其也是后续扫频振动、噪音分析精度保证的基础工作。
图-65 弹性模量与结果筛选变化过程
图-66 148次参数优化后等下弹性模量前三强
与硅钢片不同,铜线敏感度较高的弹性模量,主要为X、Y方向杨氏模量以及Z方向剪切模量。
图-67 不同模量敏感度分布
前两轮验证后,其弹性模量敏感度规律基本一致,即X及Y方向(定子径向)弹性模量,一般对本案例更敏感,则意味着后续仿真分析时,可减少设计变量数量,如从6个模量降低为3~4个,从而减少了不同模量交叉组合的可能性,从而进一步降低计算成本,或者加速等效弹性模量校准的优化效率与质量。七、写在最后
电机定子与机壳间,往往采用过盈配合方式,进行连接固定(本文案例为4组长螺栓),其接触面的宏观连接刚度,将略低于直接绑定接触的方式。一般为,在验证机壳、硅钢片、铜线的相关材料属性,均符合模态实验的基础上,通过手动调整绑定接触刚度的方式,进行验证。一般而言,推荐的接触刚度值,为0.01~0.001之间。
本文完。
作者简介:者刘笑天,仿真秀专栏作者,11年工作经验,前8年为压力容器行业的设计与分析经验,建筑环境与设备工程专业,本科学历,仿真秀科普作者。第一作者著有2部ANSYS Workbench结构仿真类书籍。第一作者申请4项发明及2项实用新型专利。声明:本文首发仿真秀App,部分图片和内容源自网络,如有不当,欢迎批评指正。欢迎分享,禁止私自转载,转载请联系我们。喜欢作者,请点赞和在看 
获赞 10108粉丝 21592文章 3547课程 219