基于轮心力法的整车路噪仿真
本文将对轮心力提取的原理和方法进行阐述,并通过轮心力加载计算得到整车路噪结果与试验测试结果进行对比,验证此技术的可靠性。
轮心力方法的关键在于轮心力的提取,轮心力提取方法有直接法和间接法。直接测量的方法带来一些困难,首先需要用到特殊测试设备,例如测压元件测量时需要承受整车的重量,而且还需要更改车轮的结构,并且也很难测量出一个频带上的动态载荷。在结构耐久和车辆动力学应用中会用到六分力测试仪,其价格昂贵,同时对操作人员要求高,由于其主要应用场景限制了其频率范围为80Hz以下的低频范围,对于整车路噪的入力提取也是不够的。那么接下来介绍一种试验和仿真相结合的手段,通过间接的逆矩阵方法提取轮心力,解决整车路噪仿真入力的问题。
轮心力法原理
路面不平度激励下的车内噪声响应分析实质是一种随机响应分析,对于线性稳定系统,如果系统的输入是随机的,并且是部分相关的,那么系统的响应也是随机的、部分相关的。在这种情况下,输入和输出分别用功率谱密度矩阵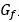 和
和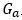 表示。对于受多个随机激励的多自由度线性系统,其随机响应计算公式为:
表示。对于受多个随机激励的多自由度线性系统,其随机响应计算公式为:
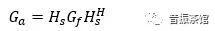 (1)
(1)
式(1)中: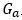 为响应PSD矩阵,
为响应PSD矩阵,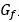 为输入PSD矩阵,
为输入PSD矩阵,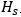 为输入点到输出点的传递函数矩阵,
为输入点到输出点的传递函数矩阵,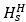 为传递函数的转置。从式(1)中,我们可以看出,有了输入激励和传递函数就可以求得响应。反过来,有了响应和传递函数,同样可以求得输入激励,计算公式为:
为传递函数的转置。从式(1)中,我们可以看出,有了输入激励和传递函数就可以求得响应。反过来,有了响应和传递函数,同样可以求得输入激励,计算公式为:
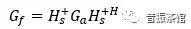 (2)
(2)
式(2)中: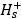 为传递函数的伪逆矩阵,
为传递函数的伪逆矩阵,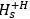 为传递函数矩阵的转置。
为传递函数矩阵的转置。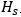 矩阵通常是一个矩形矩阵,直接求逆是不可能的,利用奇异值分解(SVD)方法实现了
矩阵通常是一个矩形矩阵,直接求逆是不可能的,利用奇异值分解(SVD)方法实现了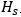 的伪逆。典型SVD如式(3)所示:
的伪逆。典型SVD如式(3)所示:
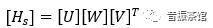 (3)
(3)
是一个M*N的矩阵,U是一个M*N的列向量矩阵,W是一个N*N的对角线矩阵,有正的或零的元素(奇异值),V是一个N*N的正交矩阵。如果我们在转向节上布置5个传感器(如图1所示),通过试验采集加速度信号,构建响应矩阵;通过CAE计算轮心到传感器位置的传递函数,构建传递函数矩阵;根据公式(2)的原理,就可求得轮心力,具体计算公式如下:
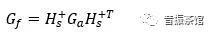 (4)
(4)
式(4)中: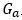 为转向节上测点加速度响应矩阵,
为转向节上测点加速度响应矩阵,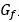 为轮心力矩阵,
为轮心力矩阵,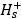 为轮心到测点传递函数矩阵的伪逆矩阵,
为轮心到测点传递函数矩阵的伪逆矩阵,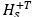 为
为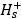 的转置。
的转置。
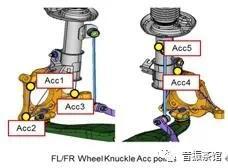
图1 转向节测点示意图
转向节振动加速度测试
加速度矩阵通过试验测试数据生成,测试道路、试验车辆状态和车速应保持跟路噪测试一致。每个道路工况至少测试三次并检查每次试验间各个测点的采集数据一致性,理论上转向节上测点加速度响应为转动自由度大于平动自由度。
为捕捉到转向节所有方向的振动,要求转向节上布置4~5个三向加速度传感器,且要求所有测点不共面,尽量远离轮心。测试布点过程中需仿真人员跟踪试验过程,记录测点位置,用于后续传函分析。同一个转向节上的所有测点需要同时采集,对于四个转向节上的测点,可以根据数采通道及传感器数量等实际情况来确定测试的批次,可分为1轮,2轮或4轮。如果分两次采集的话,建议前轮同时采集,后轮同时采集。值得注意的是,如果分批次采集的话,由于各测点非同时测量,需要额外选取一个参考加速度测点作为相位参考(不能为转向节上的5个点),此参考点应在整个试验过程中保持不动,若试验中同步采集了车内响应,也可选取车内加速度响应作为参考点,比如选取座椅导轨Z向为参考点。数据采集长度要求采样率1024Hz,分辨率为1Hz,输出各测点自功率谱,整个测试数据长度至少大于10s。转向节采集的实际加速度时域信号如图2所示。
图2 Time Domain界面预览时域图
轮心传函计算
轮心传函的计算模型为整车路噪计算模型,由于转向节加速度响应测试信号中已经包含了轮胎的影响,因此在传函分析模型中应除去轮胎。
轮心传函矩阵通过CAE计算的轮心(图3所示制动盘与转向节轴承连接位置)到测点位置传递函数生成,每个轮心需要考虑6个自由度(X,Y,Z,RX,RY,RZ)激励,共24个工况,响应点必须包含各转向节上的加速度测点。计算模型中减振器处于unlock状态,底盘衬套参数采用0~300Hz的随频率变化的动刚度和阻尼,也可采用100Hz频率下的动刚度值。
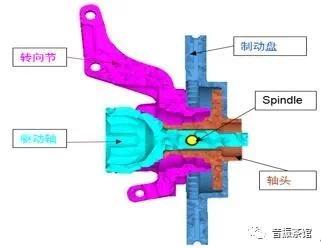
图3 轮心结构示意图
轮心力计算
有了加速度矩阵和传递函数矩阵就可以进行轮心力计算,计算流程如图4所示。
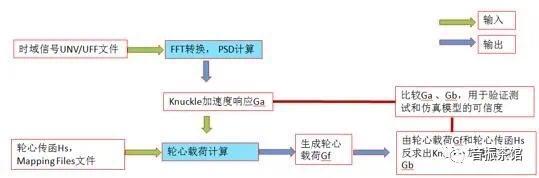
图4 轮心力计算流程图
伪逆过程的准确性是获得质量结果的关键,因此计算得到的轮心力还需要进行验证。为了检查矩阵的SVD求逆的准确性,用计算的轮心力和传递函数,求得响应点加速度矩阵,通过将轮心力计算的加速度和测试得到的加速度进行对比,如图5所示,和之间error越小,表明转向节测试数据和整车有限元精度高,并且足以准确地预测轮心力,一般要求的error值小于0.4即可,如果部分通道的error值大于0.4,需要去除这些通道,直到所有通道的error值小于0.4。
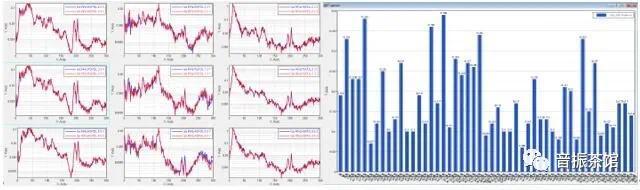
图5 Ga和Gb比较
最终计算得到的轮心力如图6所示,一般来说,计算得到的轮心力为轮心力的PSD矩阵,是一个非确定性信号,通常需要再进行主向量(PCA)分解,去掉轮心力的相关性,将非确定性信号转化成确定性信号,以便后续进行TPA,贡献量等分析。
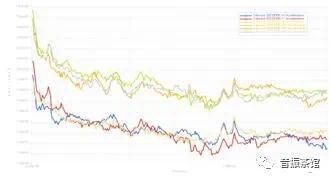
图6 轮心力计算结果
基于轮心力的整车路噪仿真
经过逆矩阵法最终得到了一个较为准确的轮心力,此轮心力包含24个主向量,这些向量是线性无关的。将轮心力加载到整车路噪模型中,仿真计算得到路噪响应曲线,最终的车内路噪响应是将这24个分量工况分别得到的响应进行RSS。通过仿真与实车测试曲线对比,检验模型和载荷提取的准确性,最终的路噪仿真结果与试验结果相比如图7所示。
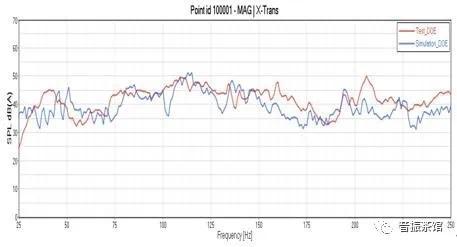
图7 基于轮心力的整车路噪仿真结果
总结
基于轮心力法的路噪仿真,将轮胎这个高度非线性,难模拟的子系统绕过,通过仿真与试验的对标验证,证明了轮心力的提取和路噪仿真分析的可靠性,为整车路噪开发提供了一种快速有效地评价手段。但此方法仅适用于存在样车的开发阶段,存在一些局限性。后续将讲述基于NVH虚拟路面和CDTire的整车路噪仿真,敬请期待!
参考文献:
[1] Perry Gu, Joe Juan, Archie Ni and James Van Loon, “OperationalSpindle Load Estimation Methodology for Road NVH Applications” ,SAE,2001-01-1606
[2] Brian Y. Cho, “Spindle Load Application for NVH CAEModels by Using Principal Vector Approach” ,SAE, 2005-01-1505
[3] 李京福,王吉祥,等。轮心力提取在整车路噪仿真中的应用[C],Altair技术大会论文集,2019。【免责声明】本文经授权转自音振茶馆(ID:River666_2020),由钱总原创,版权归原作者所有,仅用于学习!对文中观点判断均保持中立,若您认为文中来源标注与事实不符,若有涉及版权等请告知,将及时修订删除,谢谢大家的关注!





