【励分享】LiToSim几何非线性屈曲分析-弧长法
结构非线性问题可分为三大类:几何非线性、材料非线性和状态非线性。其中几何非线性是因几何变形引起结构刚度改变的一类问题,即结构的平衡方程必须在未知的变形后的位置上建立。几何非线性问题常采用Newton-Raphson迭代进行求解,但Newton-Raphson迭代无法求解荷载位移曲线具有荷载极值点的情况,这时可采用弧长法(Arc length method)求解。
LiToSim是一款完全国产自主可控,具有国际先进水平的通用有限元软件。LiToSim具有强大的非线性分析能力,已具备完全国产自主可控的弧长法,可广泛应用于复杂几何非线性问题的CAE分析中。同时经过案例对标验证,LiToSim弧长法的求解结果与主流商用软件计算结果相当。
圆弧拱失稳问题的荷载位移曲线比较复杂,常用来检验弧长法。如图1所示,两端铰接的深拱结构承受拱顶中心集中力作用,采用平面梁单元,梁的截面形状为矩形。
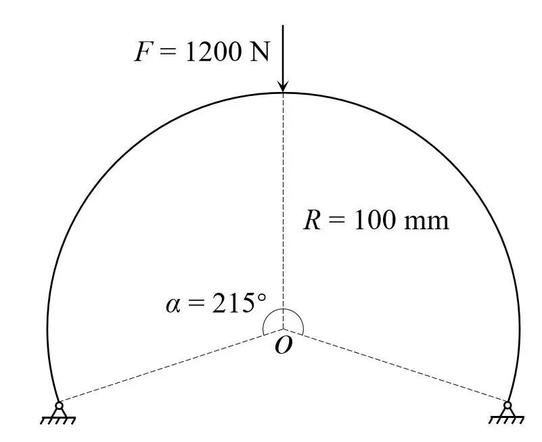
图1. 深拱结构承受拱顶中心集中力作用的模型示意图
创建新工程项目并导入网格。首先启动LiToSim,点击菜单栏文件→新项目,弹出新工程项目对话框,如图2所示。在弹出的对话框中选择分析类型:固体力学→静态,点击确定;

图2. 新建工程项目
左侧模型树网格模块处单击鼠标右键,选择导入,将网格文件(CircularArch1.msh)导入工程中,如图3所示。
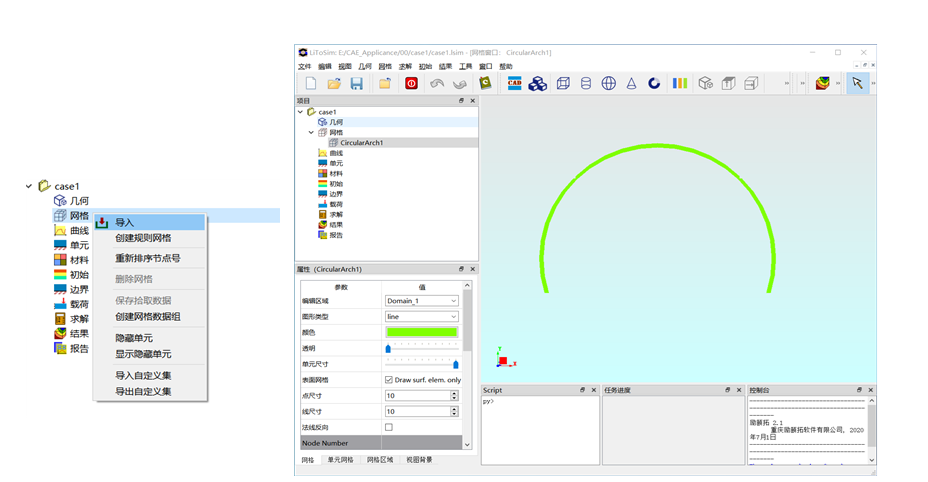 图3. 导入网格文件
图3. 导入网格文件
赋予单元类型。在模型画布中单击鼠标右键,选择拾取单元→单元,在弹出的对话框中指定选择模式→方框,在模型画布中框选全部单元,如图4所示;

图4. 选择单元示意图
然后,在左侧模型树单元处单击鼠标右键,选择单元类型,在弹出的单元类型编辑对话框中,选择单元类为Beam2D,单击Edit,设置梁单元截面形状和尺寸参数,参数设置如图5所示,点击确定。
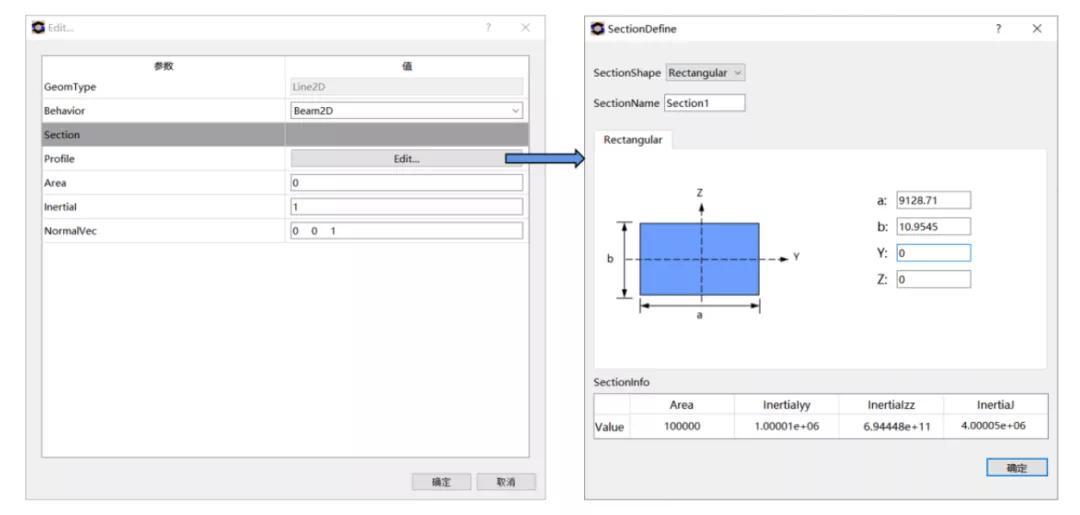
图5. 设置单元类型相关参数
设置材料模型。左侧模型树材料模块处单击鼠标右键,选择指定材料,在弹出的材料库对话框中选择弹性→各向同性→新项目,编辑材料参数如图6所示,点击设置,然后点击确定。
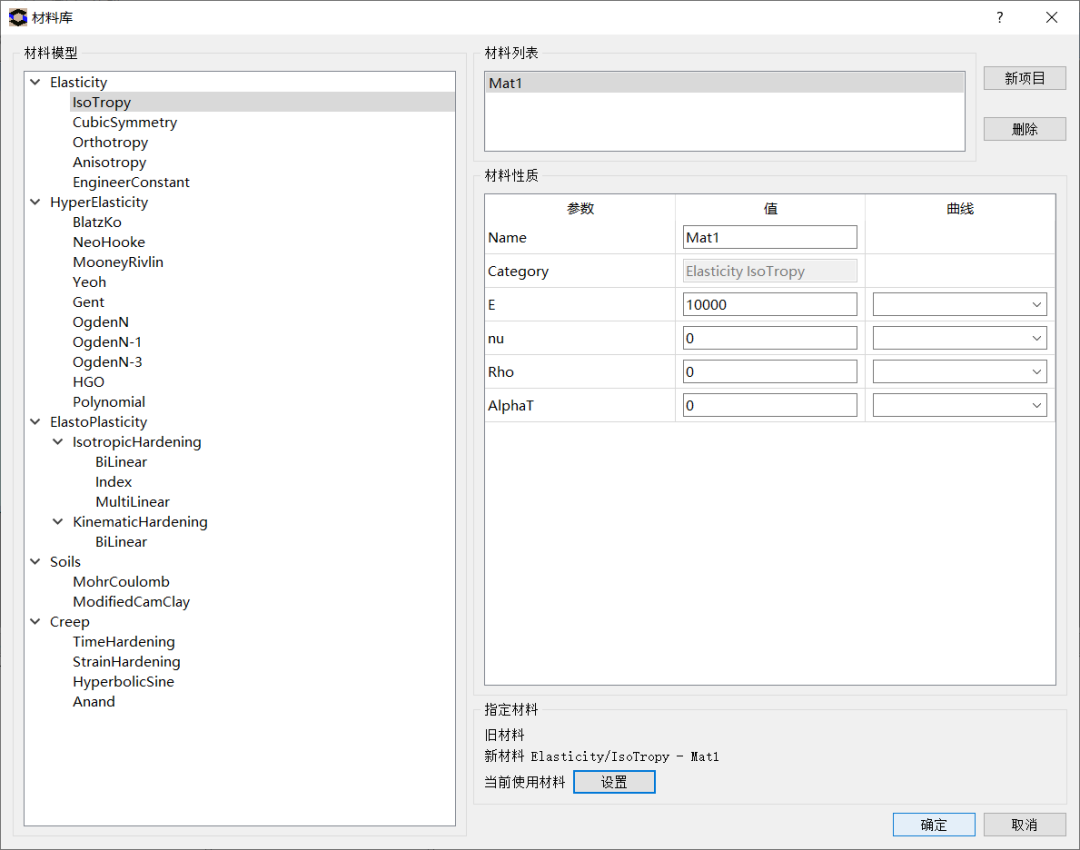
图6. 设置材料参数
设置模型边界条件。分别选中拱的两个端点,并在左侧模型树边界模块处单击鼠标右键,选择位移,均采用铰支约束,即X和Y方向的位移Ux和Uy为零,如图7所示。
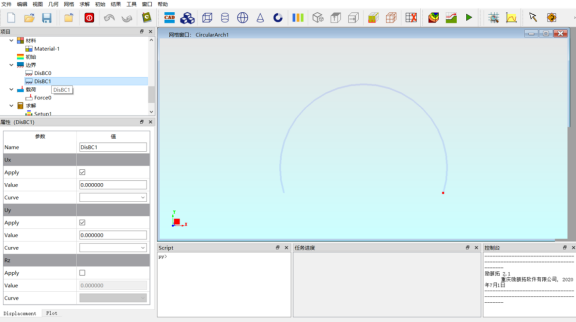
图7. 设置边界条件
设置载荷条件。选中拱顶点处的节点,在左侧模型树载荷模块处单击鼠标右键,选择节点力,设置拱的顶点承受沿Y轴负方向的中心集中力,如图8所示。
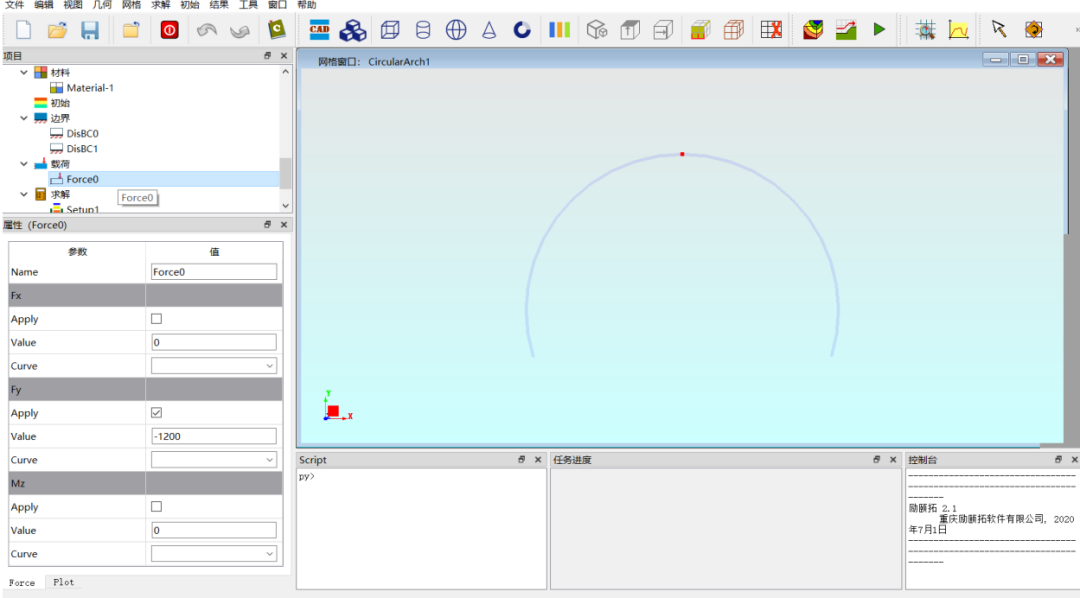
图8. 设置载荷条件
设置弧长法求解控制参数。在求解模块单击鼠标右键,进行求解参数设定:打开求解器控制窗口,打开大变形并选择弧长法,设置相关参数如图9所示。设置好后,在左侧模型树Setup1处单击鼠标右键选择求解,提交求解器进行计算。
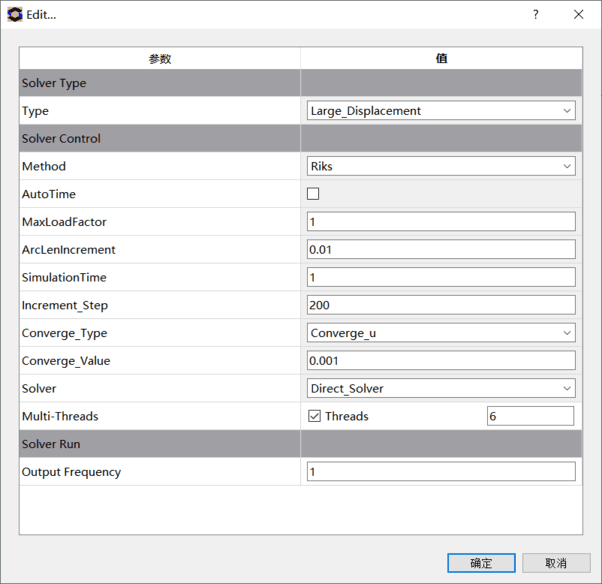
图9. 设置求解控制参数
等待求解完成后,查看求解结果。点击结果→创建云图,选择Y向位移分量UY,如图10所示,然后确定,即可查看云图;同时,点击UY→创建动画,即可查看变形动画,如图11所示。
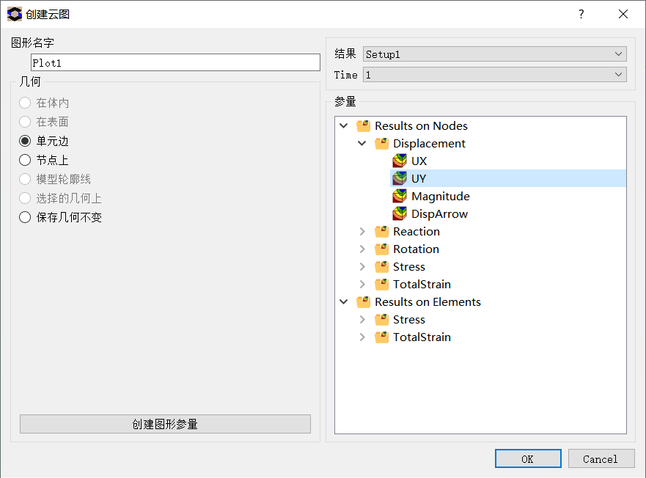
图10. 创建UY云图

图11. 创建UY动画
ABAQUS计算的动图结果如图12所示,可以看出LiToSim与ABAQUS计算的结构形状变形趋势一致,最大最小值范围误差较小。同时,荷载作用点处的荷载位移曲线对比如图13所示,二者基本一致,说明LiToSim求解结果与ABAQUS基本相同。
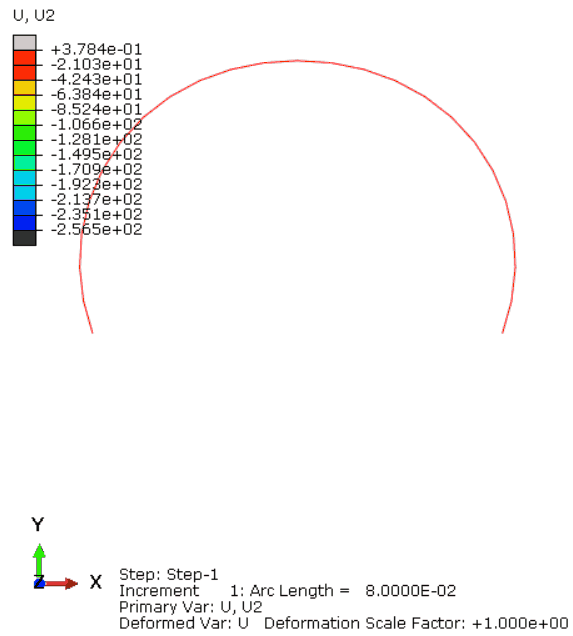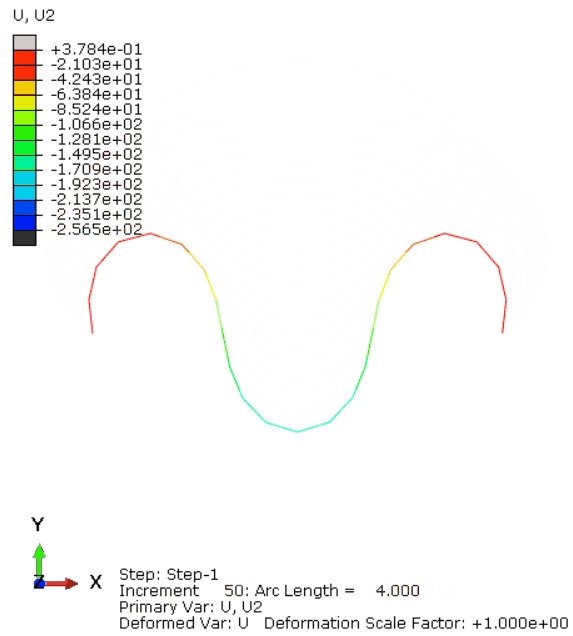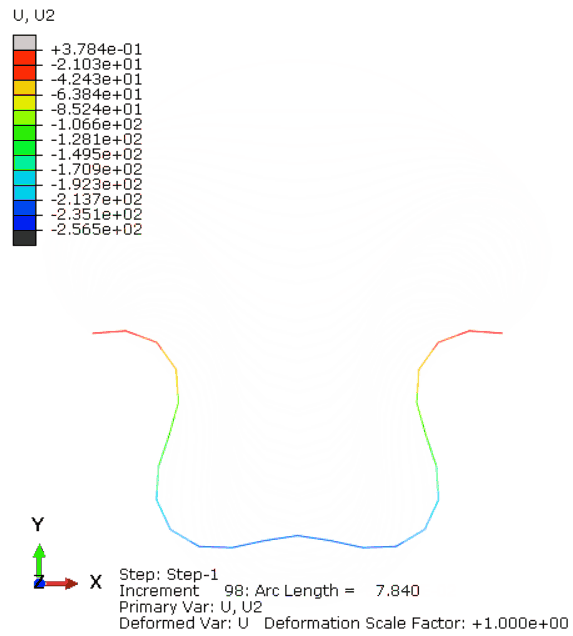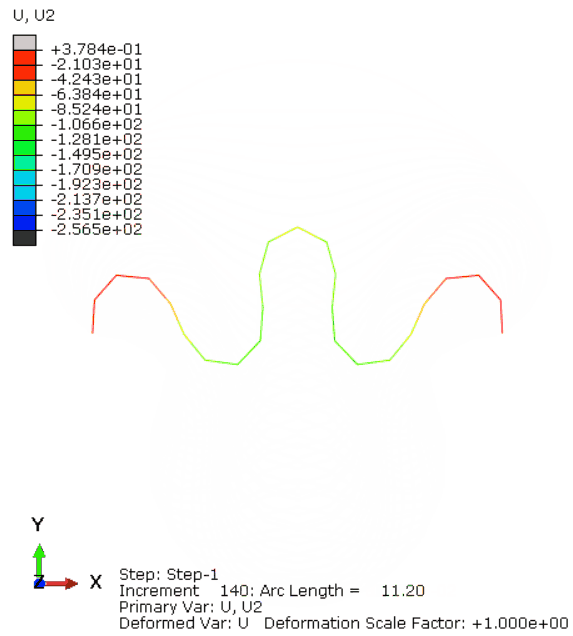
图12. ABAQUS的UY动画
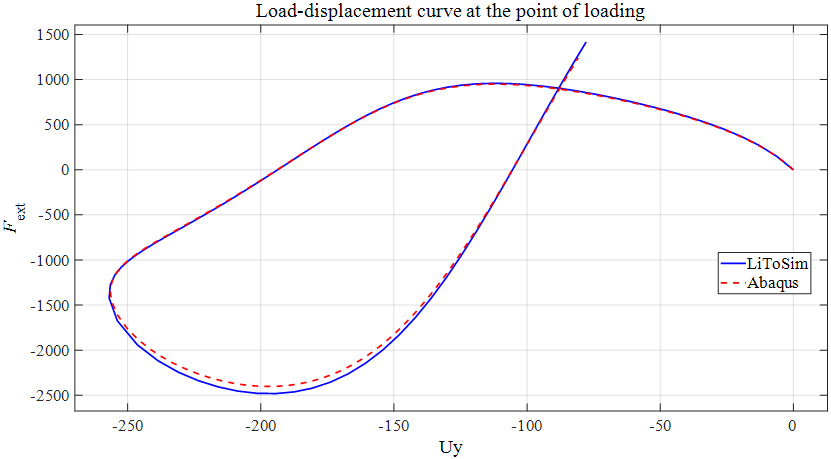
图13. 深拱结构承受拱顶中心集中力作用的荷载位移曲线对比
算例2为扁拱结构承受拱顶中心集中力作用,如图14所示,LiToSim与ABAQUS计算结果对比如图15-16所示。
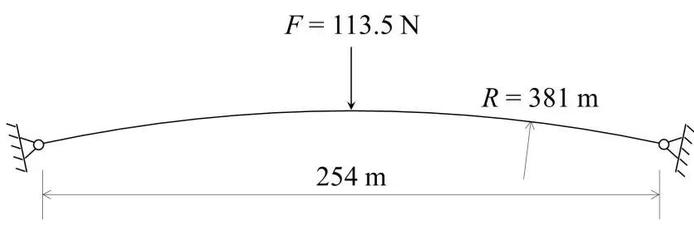
图14. 扁拱结构承受拱顶中心集中力作用的模型示意图
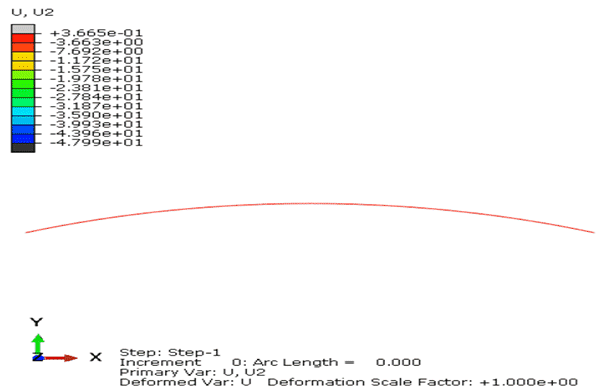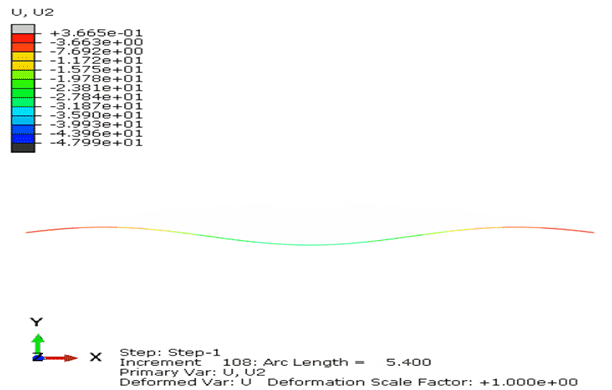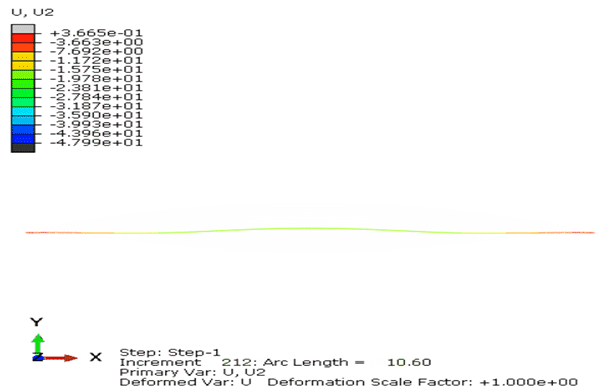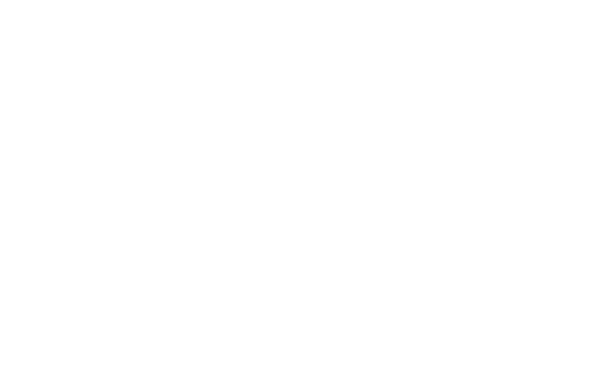

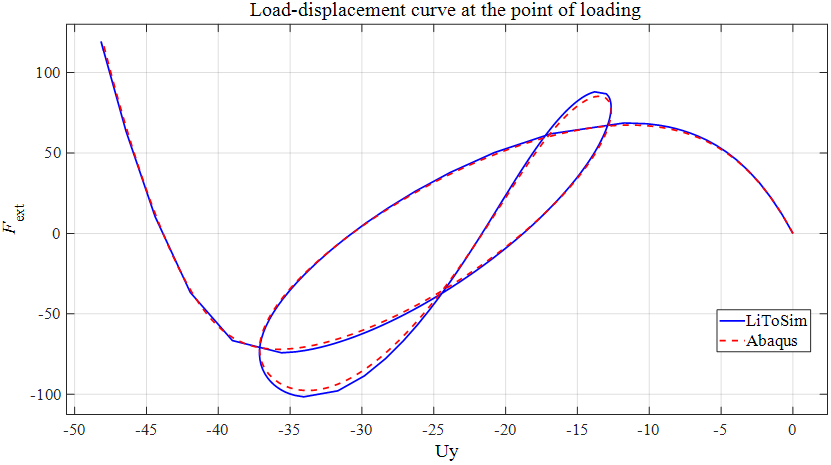
图16. 扁拱结构承受拱顶中心集中力作用的荷载位移曲线对比
算例3与算例2模型相比,只将拱顶中心集中力改为拱顶偏心集中力,偏移量为1°,LiToSim与ABAQUS计算结果对比如图17-18所示。
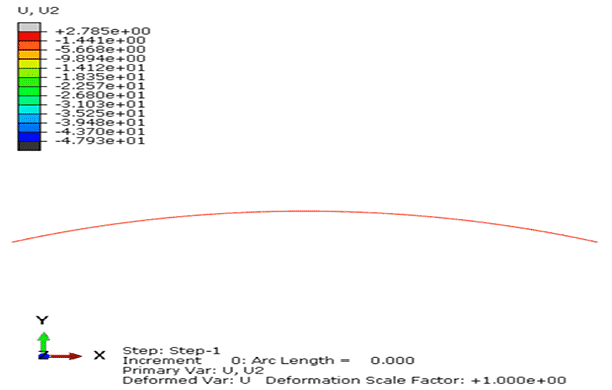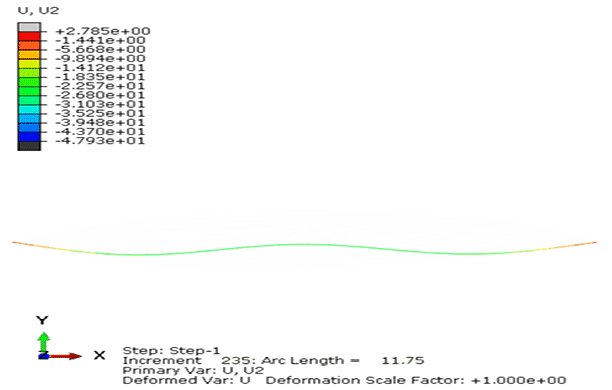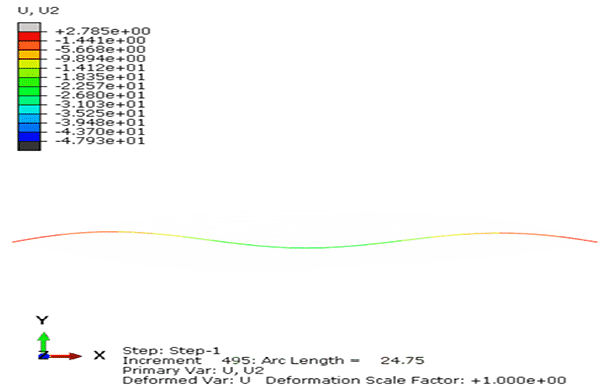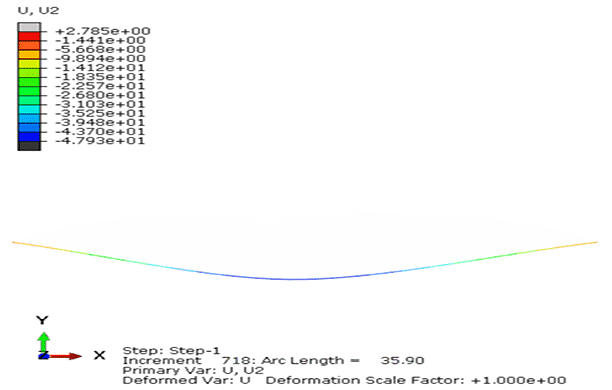
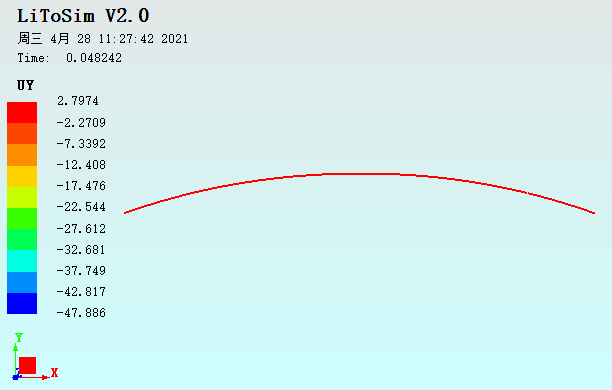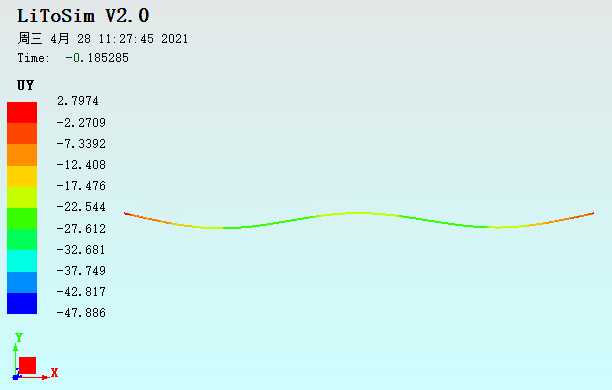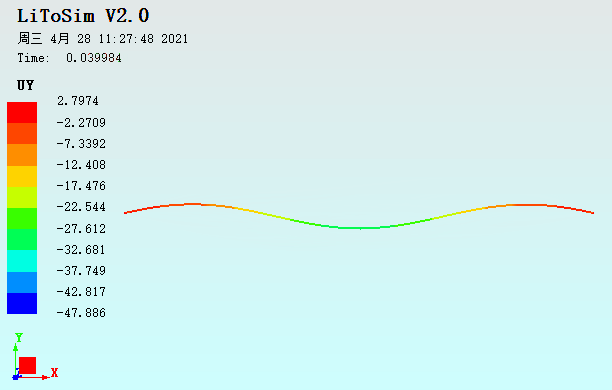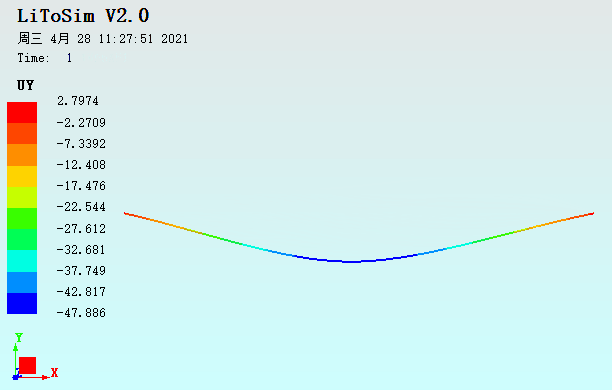
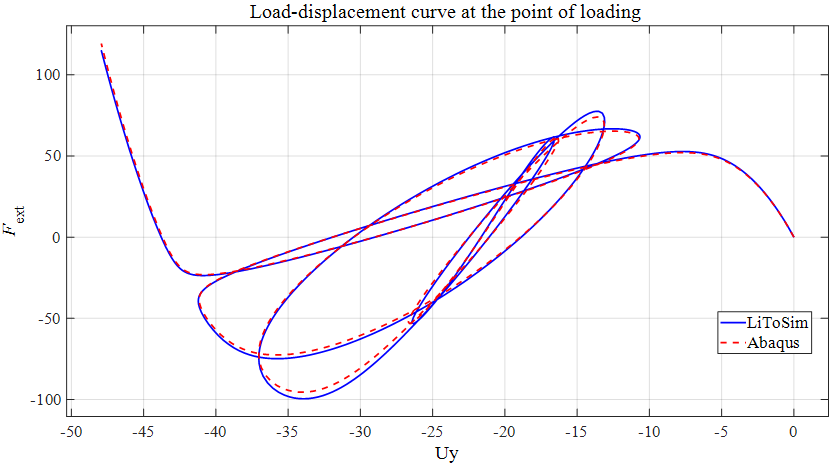
图18. 扁拱结构承受拱顶偏心集中力作用的荷载位移曲线对比
算例4为扁拱结构承受拱顶偏心集中力作用,如图19所示,采用壳单元进行模拟,集中力施加在壳单元边缘节点上。LiToSim与ABAQUS计算结果对比如图20-21所示。
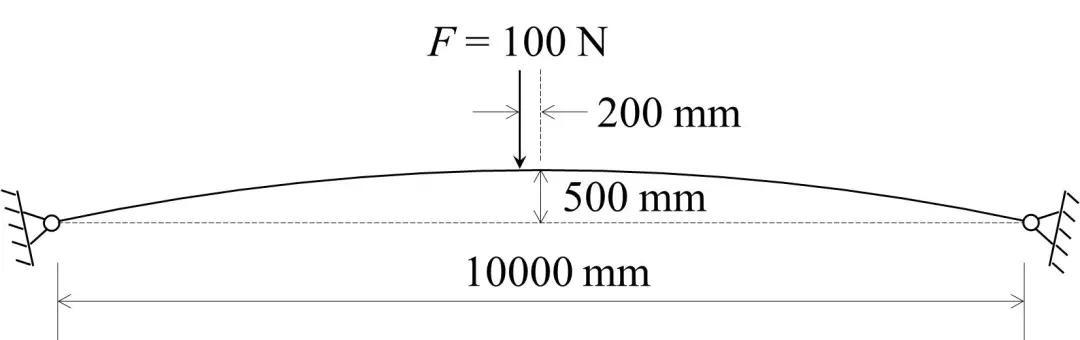
图19. 扁拱结构承受拱顶偏心集中力作用的模型示意图

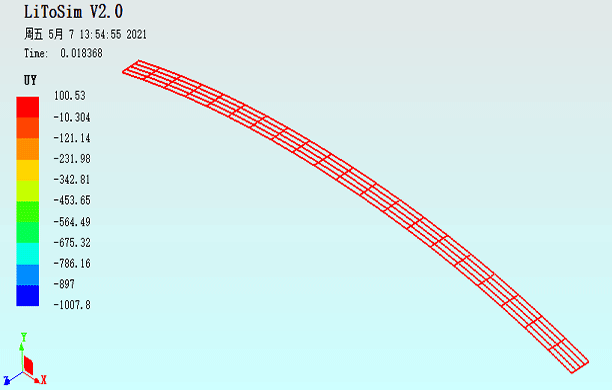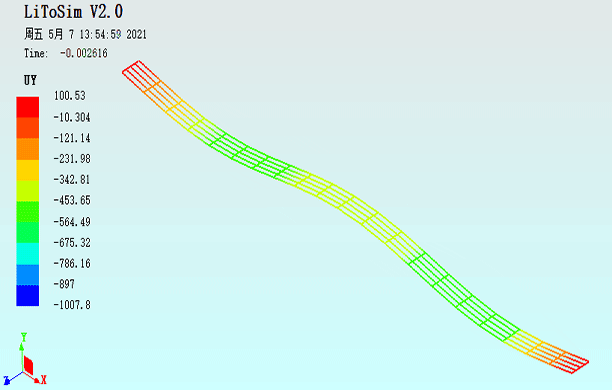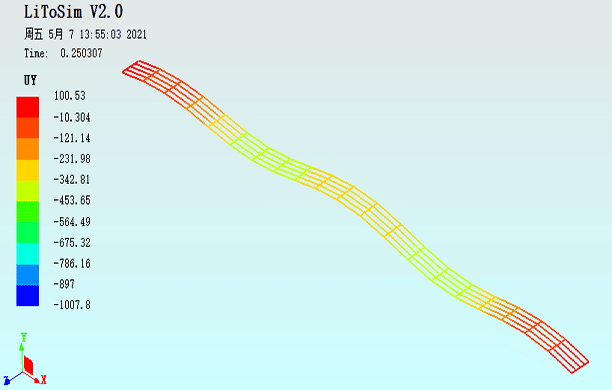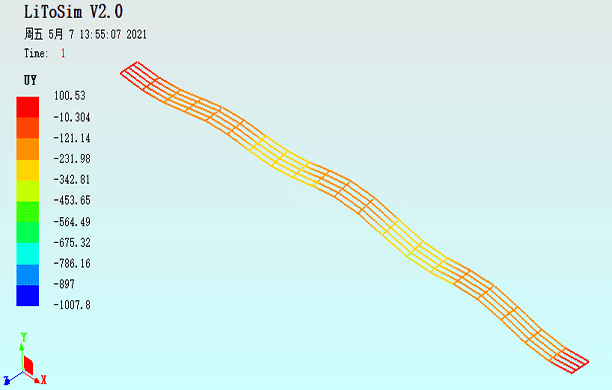
图20. 扁拱结构承受拱顶偏心集中力作用的UY动画

图21. 扁拱结构承受拱顶偏心集中力作用的荷载位移曲线对比
通过算例验证LiToSim所具备的弧长法与主流商用软件计算结果相当,可被广泛应用于实际工程几何非线性问题CAE分析的评估中。
感谢西南交通大学对文中ABAQUS计算结果提供的支持。





