电机电磁人的学习笔记:振动与模态
本文摘要(由AI生成):
本文主要介绍了力学平衡方程、振动分析、模态分析、自由模态与约束模态等内容。其中,振动分析是动力学分析中的一种,模态分析是振动分析的特例,也是振动分析的基础。模态分析公式为特征方程,其特征值为固有频率,特征向量为振型。振动方程的解是模态方程解与特解之和。在计算振动时,认为系统是线性的,就可以采用模态叠加法,计算结构在不同激励下的振动情况。
1、力学平衡方程
静力学平衡方程:
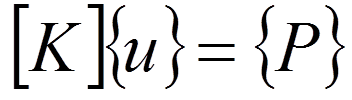
动力学平衡方程:

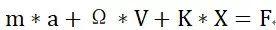
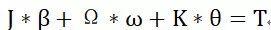
式中,[M]—结构的总质量矩阵;
[C]—为阻尼矩阵;
[K]—结构的总刚度矩阵;与结构、约束条件、材料等有关
[u]—结构的位移向量;
{R(t)}—强迫力列阵。
2、振动分析
振动分析是动力学分析中的一种,振动分析过程中假设阻尼矩阵为0矩阵,此时不考虑速度项对结构的影响,由此振动分析的动力学公式变化为:
3、模态分析
模态分析是振动分析的特例,也是振动分析的基础。
模态分析是振动分析中不受外力的情况(不受外力不是没有约束)。因此在模态分析中,振动分析公式的等式右侧为零,即:

因此模态分析公式为:

其特征方程可以写为(鉴于高数其次二阶常系数微分方程解法)

其特征值问题
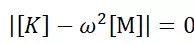
其中 特征值 为固有频率
特征向量为振型
4、为什么说模态分析是振动分析的基础
对比模态分析公式和振动分析公式
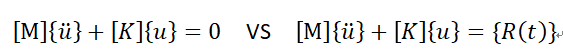
从微分方程的角度看,可知模态方程是振动方程的常系数形态,因此模态方程的解是振动方程的通解,振动方程的解是模态方程解与特解之和。
因此我们在计算振动时,认为系统是线性的,就可以采用模态叠加法,计算结构这不同激励下的振动情况。
从物理现象上理解,模态方程反应自身结构特征,其特征值为自身结构的各阶固有频率,特征向量反应各阶振型。
当施加不同频率的外力时,结构根据外力频率和作用点、方向等因数,激发出相应的固有频率,而与外力频率相差较大或者作用方向不同的固有频率和振型将不被激发,因此振动方程反应特定条件下结构的振动。
5、为什么不考虑阻尼的时候结构一定是做振动的
从模态公式可以得出,其特征仿真的解为
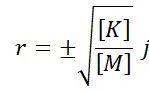
其中 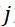 为虚数向量。这里的解即为特征值:
为虚数向量。这里的解即为特征值:

根据这个特征方程的解我们可以得到模态方程的通解形式为

可以看到模态方程的解是一个关于u关于t的正余弦的代数和,也就是说位移u随着时间t的变化为各中频率下正余弦的振动之和。
刚才已经讨论过了,振动方程的解为模态方程解的特解,因此振动方程的解也一定是各频率结构振动的过程。
6、结构的频率和振型VS自由度
结构的频率和振型的数量,与结构的自由度的数量有很大的关系。
7、什么是结构的自由度
我们通常认为一个物体的自由度有6个,三个方向的平动和三个轴的转动,这是建立在这个物体是刚体的前提下,注意刚体是没有震动问题的。
在振动分析中,我们认为结构体非刚体,才来计算他的振动特性。这里要注意到所选单元的特性问题:
实体单元:节点上三个自由度,无转动自由度,弯曲是通过单元的拉伸和压缩排布实现的(实体单元的面必须是平面,可以做拉压变形,不能弯曲);这可能是造成自由模态是前六阶自由度出现非零项的原因。
梁壳单元:节点上六个自由度,具备转动自由度,在做振动分析时,可以根据结构特点,尽可能选择这种单元进行振动分析,会更为准确。
自由度与频率和振型
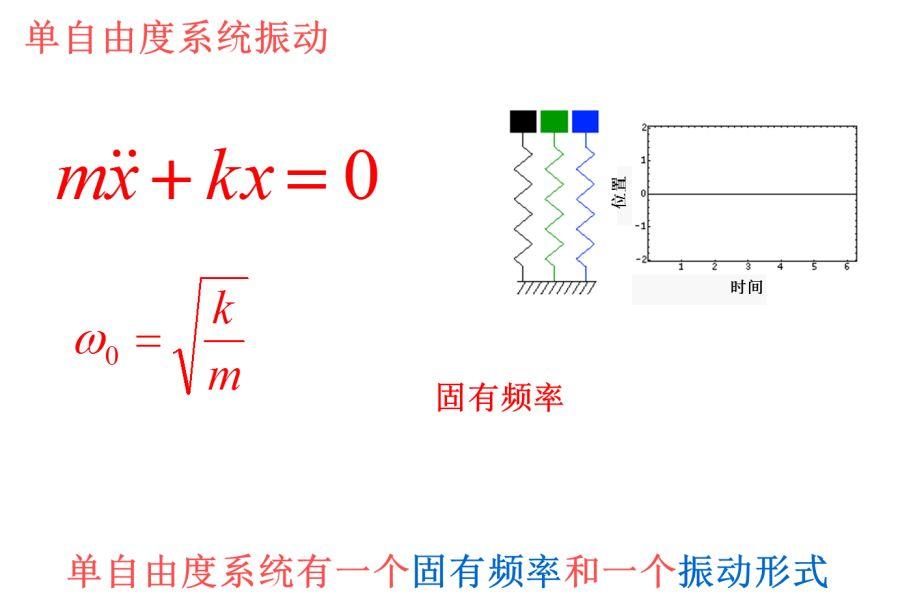
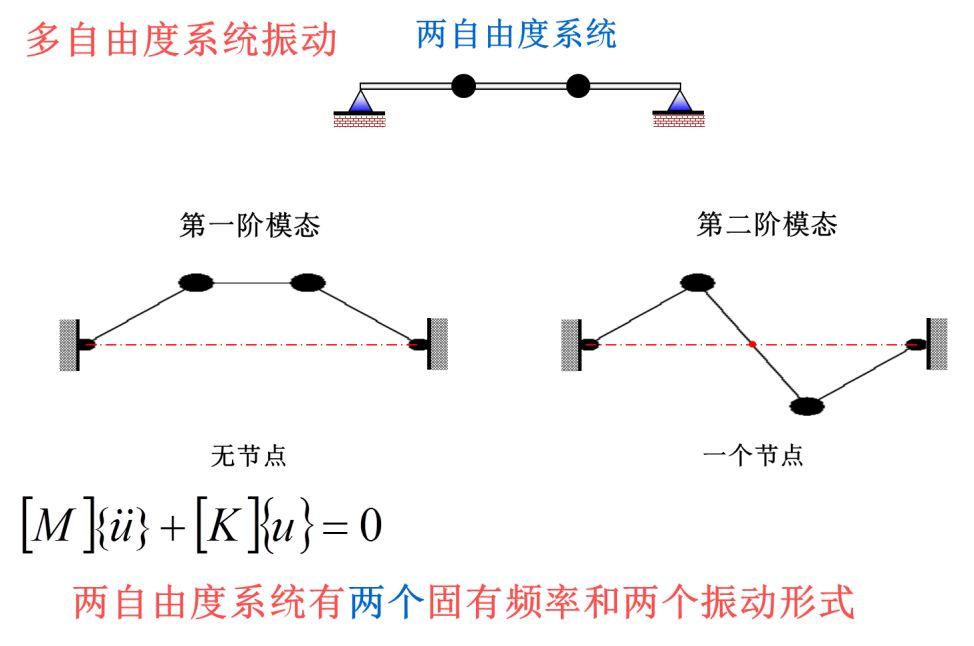
有多少个自由度?有多少个频率和振动形式
8、模态的阶数
结构在不同方向刚度大小决定了这些方向发生振动的难易度,按照由易到难结构固有频率由低到高,对应的,分别称为一阶\二阶\三阶模态等等
模态的阶数与物体振动的振型有关
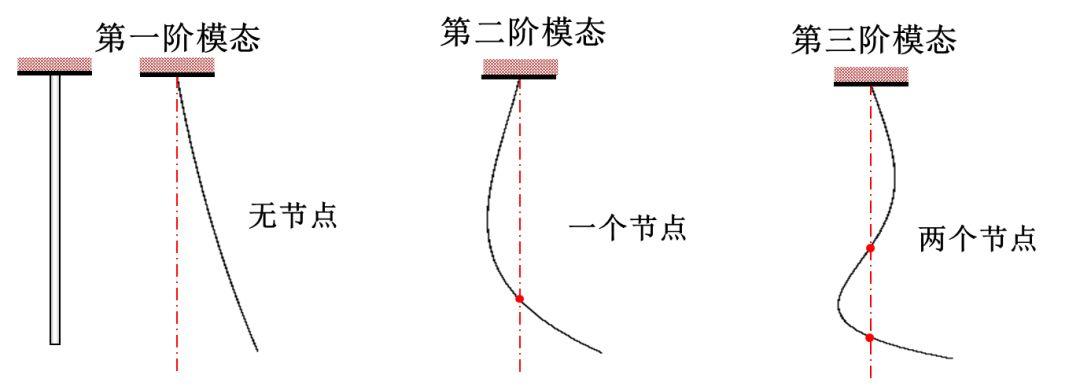
约束模态下的一阶模态
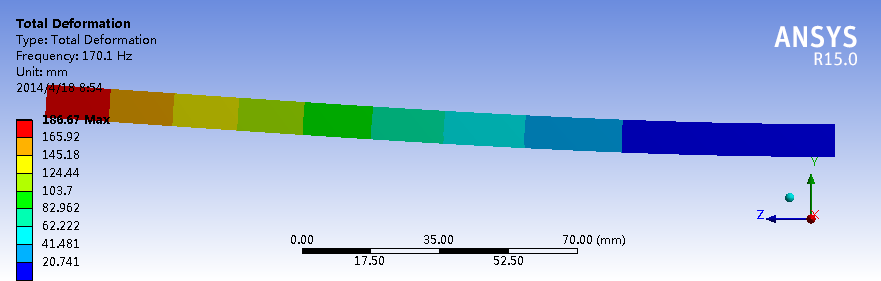
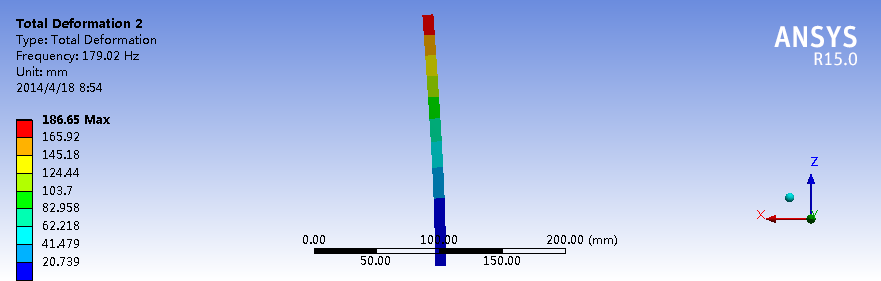
约束模态下的二阶模态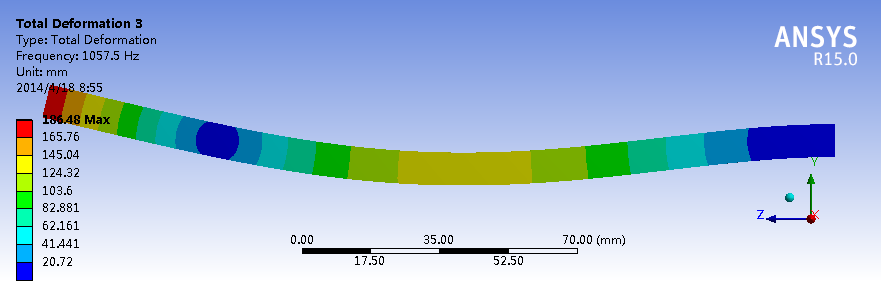
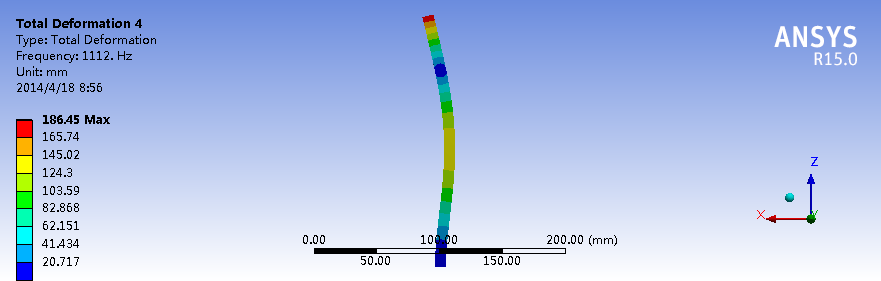
约束模态下的三阶模态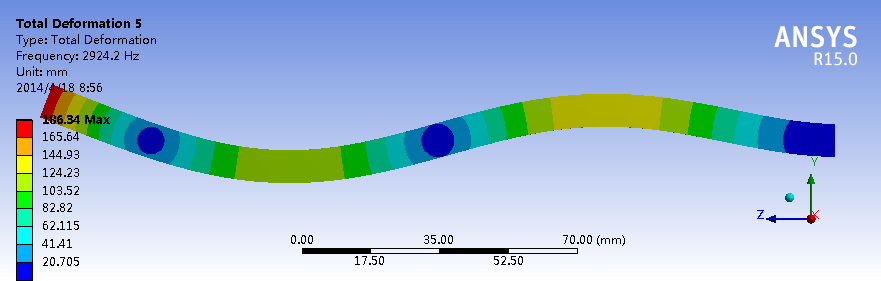
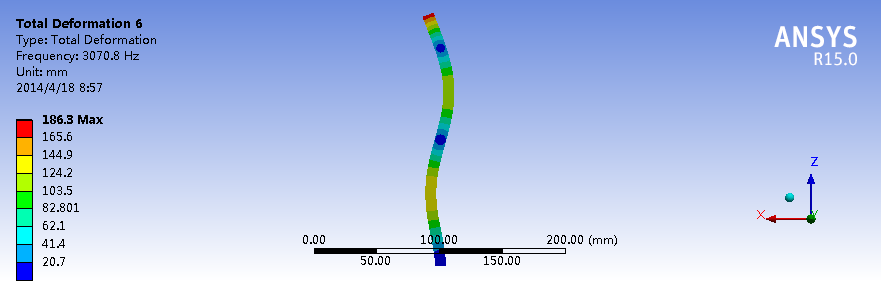
对于这种一端约束的长直梁结构,X和Y方向的刚度相似,Z方向最不容易变形,因此一阶、二阶、三阶模态分别有两个振型,即X、Y方向各一个,固有频率也非常接近。
再看一个框架的约束模态分析的结果。
一阶模态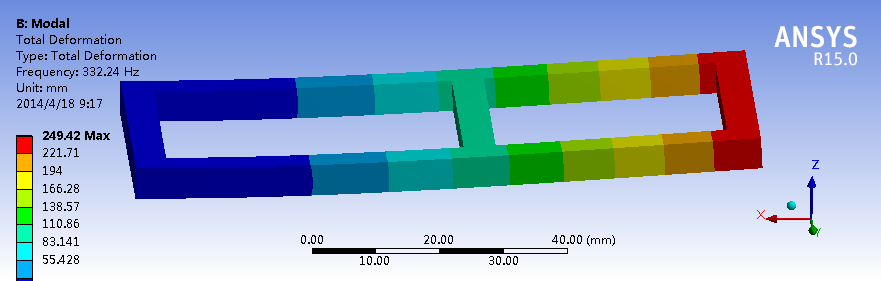
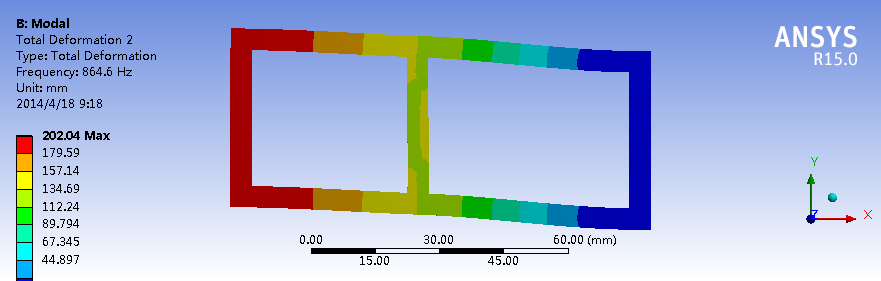

二阶模态
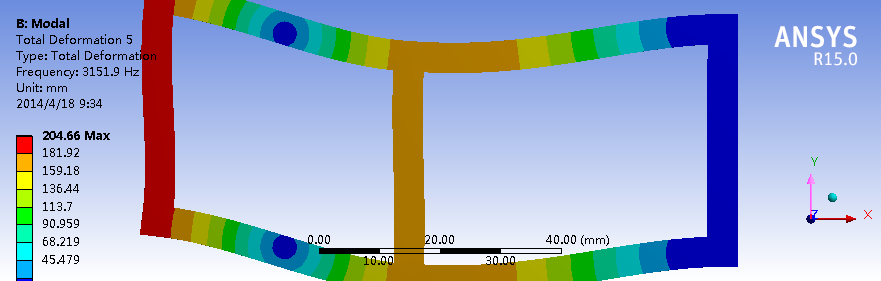
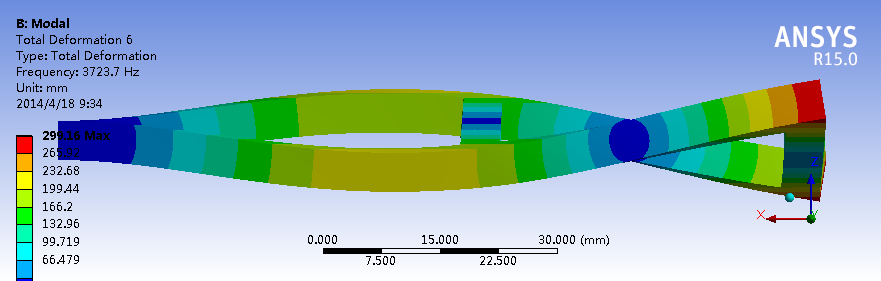
对于这个框架结构,Z方向的刚度最弱,因此一阶模态中,最低频率时的振型为结构在Z方向上下摆动;Y方向的刚度略强于Z方向,因此一阶模态中振动的模态略高与Z方向的振动;最强的是X轴方向的扭转,在一阶振动中振动的频率更高。二阶模态与一阶模态的振型相似,特点是变形的“波长”比一阶模态短(是否是由于频率增加导致)。
9、自由模态与约束模态
模态的计算可以根据情况分为自由模态和约束模态两种。自由模态是指物体在无约束状态下的模态形式;约束模态指的是在一定的约束状态下进行模态计算得到的模态形式。
自由模态适用于对飞机、火箭等处于自由空间中,无约束条件的物体。
约束模态适用于处于某约束条件下的物体,如发动机、电子设备等
在进行振动分析时,需要根据实际条件选择相应的模态分析结果。因为,从公式上分析,两种模态采用的公式虽然相同,

但是,由于约束条件会影响到公式中的刚度矩阵K,因此两种情况属于各自的分析方程,并不存在谁是谁的子集的说法。从计算的结果也可以看出,对同一个结构进行自由模态和约束模态两种分析,得到的频率结果如下:
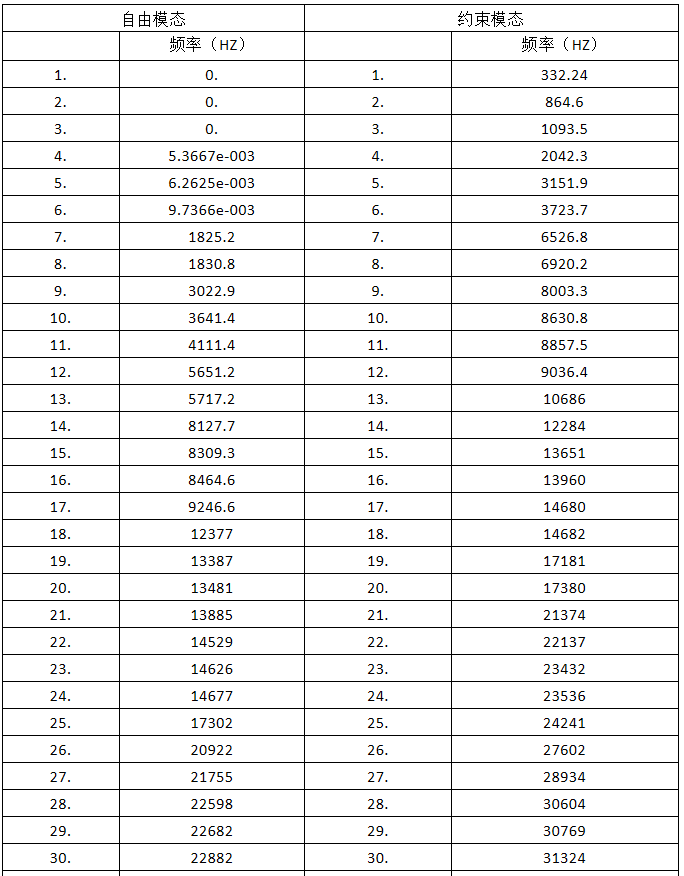
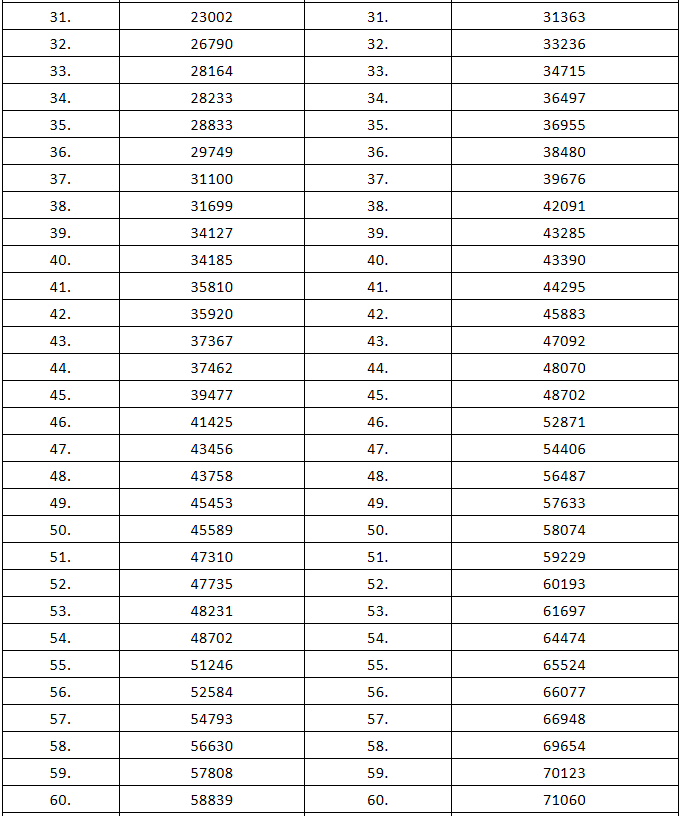

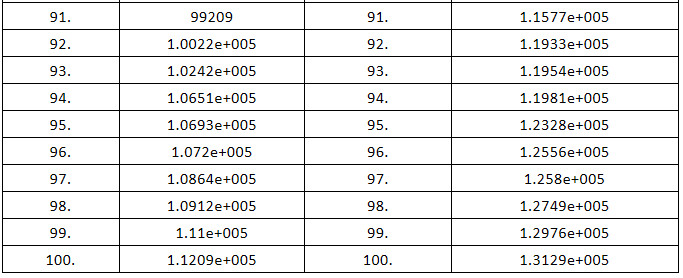
可以看到自由模态和约束模态之间无任何对应关系,因为是两个方程组各自的解。
如果在计算振动时采用模态叠加法进行分析,如我们之前讨论的结论,振动分析是模态分析的特解,因此在进行相应振动分析时,要采用各自的模态,才能得到准确的结果。
下面以一个长直梁为模型,分别采用自由模态下的振动激励、约束模态下的振动激励、全模态法三种谐响应分析方法和一个瞬时结构分析进行计算,所加激励力为10幅值下的振动力,取30HZ的频率激励,分别计算结果如下:
自由模态法(振动分析时无法加约束)
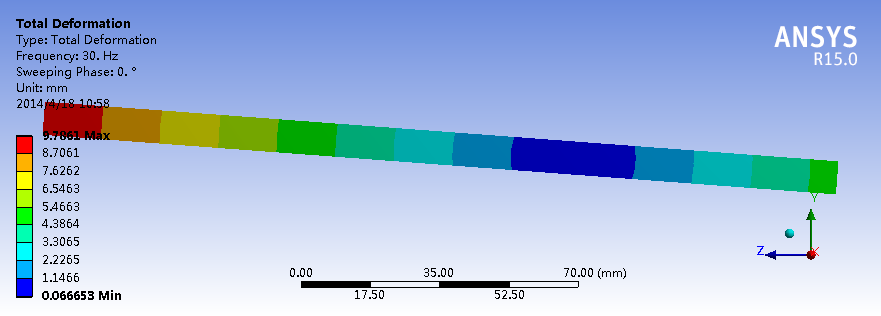
约束模态法
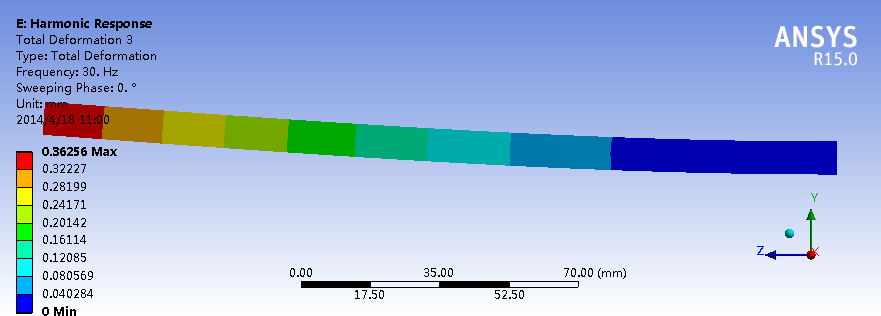
全模态法
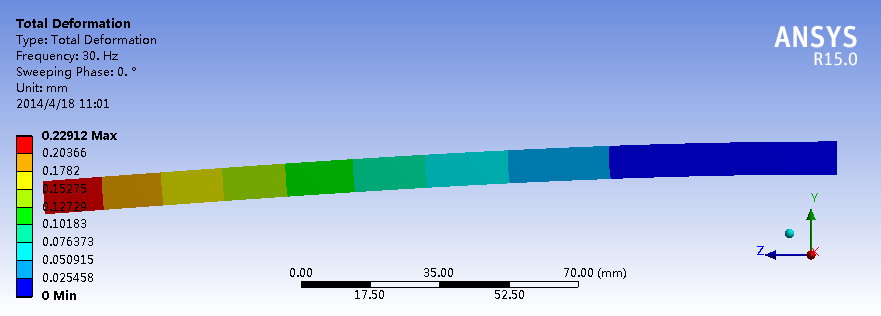
瞬态结构场
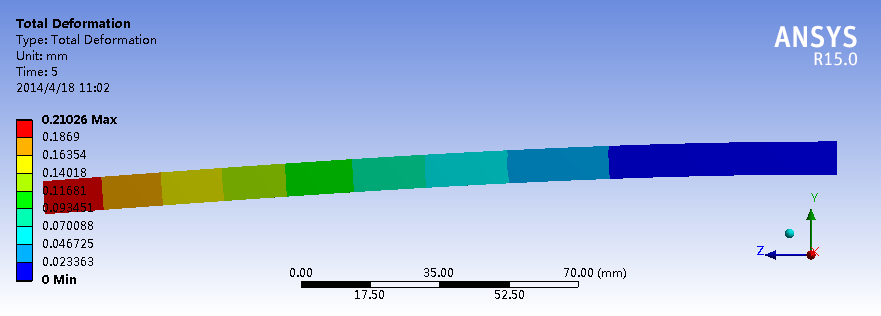
对比这几个仿真结果可以看出,就振幅的最大值来看,瞬态结构场计算的结果和全模态法比较接近,约束模态法计算结果与前两者在同一数量级且偏大。自由模态法无论从振型还是幅值,与三者相差都很大。
我认为瞬态结构场计算的更为准确(因为其对全微分方程进行直接求解);全模态法对全矩阵进行求解,无须选择模态阶数,对质量矩阵不做简化,因此计算结果比较接近瞬态场的计算结果,比较可信;采用模态叠加法是在一定阶数模态分析基础上进行叠加得到的(本算例Y方向模态有效质量已经达到0.990885),忽略了部分模态的影响,但是计算速度较快。
作者:白增程,仿真秀专栏作者(ID:化凡人生),硕士,沈阳工业大学,电机电器专业,擅长电机及相关产品的仿真分析,10年工程仿真经验。
声明:原创文章,首发仿真秀,部分图片源自网络,如有不当请联系我们,欢迎分享,禁止私自转载,转载请联系我们。








