材料力学之圆轴扭转时的应力
来源:力创空间(ID:mechanics786),作者:蔺斯诺 李运杰。
横截面为圆形的直杆受扭时的应力,需要综合研究几何、物理和静力等三方面的关系。以下是我们研究的一个思路。
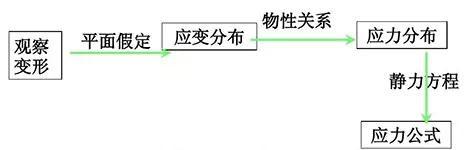
确定横截面上切应力的方法与过程
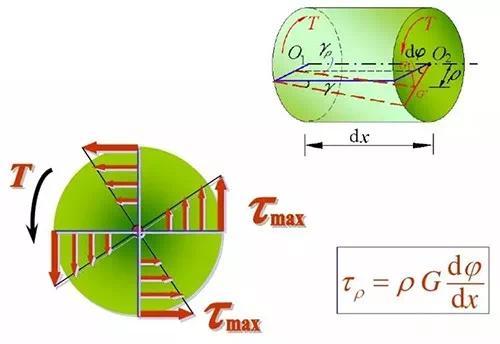
在轴表面作圆周线和纵向线,在扭转力偶矩作用下,圆周线长度形状不变,各圆周线间距离不变,只是绕轴线转了一个微小角度;纵向平行线仍然保持为直线且相互平行,只是倾斜了一个微小角度。变形如图所示。
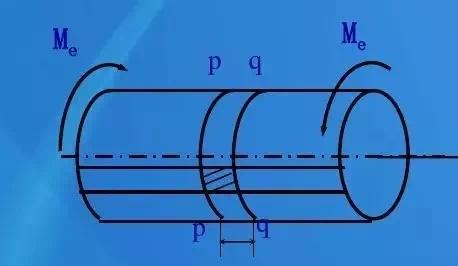
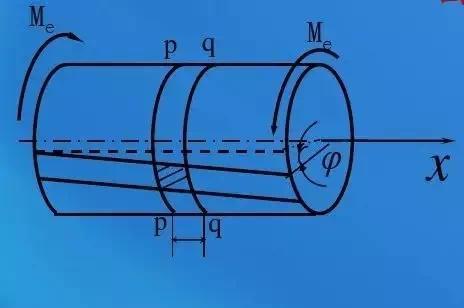
圆轴扭转的平面假设:圆轴扭转变形前原为平面的横截面,变形后仍保持平面,形状和大小不变,半径仍保持直线,且相邻两截面间的距离不变。
这里需要注意,一定要在线弹性范围内。接下来研究用到了切变模量、切应力互等定理、剪切胡克定律等知识。
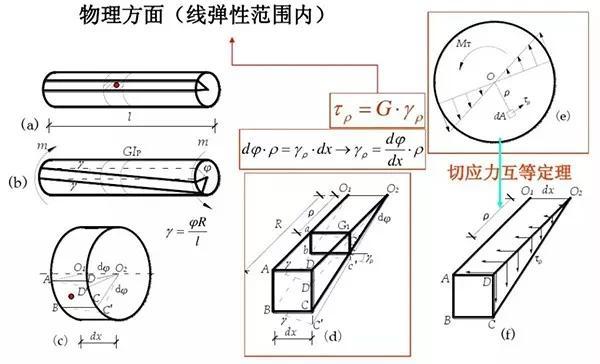
1、变形协调方程推导应变、应力分布规律
设到轴线任意远ρ 处的剪应变为γ(ρ),则有如下几何关系:
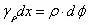
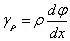
式中,dφ/dx 为扭转角沿长度方向变化率。
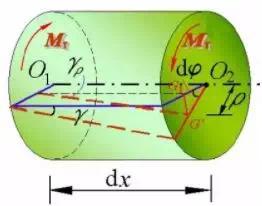
距圆心为ρ 任一点处的γρ、τρ 与到圆心的距离ρ 成正比。
2、物性关系——剪力胡克定律
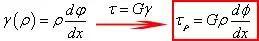
至此,我们已经求出了切应力的表达式,但是扭转角沿长度方向的变化率还不知道。这就需要静力学方程来解决了。
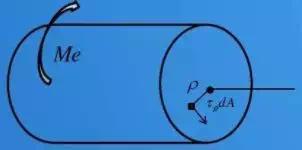
微分面积:
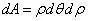
dA 上的微内力对圆心的力矩:
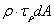
对上式进行积分(扭矩定义):
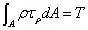
横截面上的扭矩应与截面一侧的外力偶距相平衡
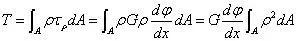
我们引入一个极惯性矩
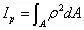
式中,Ip 为横截面对形心的极惯性矩(截面二次极矩,单位为m4)。
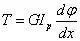
在圆截面边缘上有最大切应力:
令
抗扭截面系数(单位:m³)
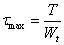
公式适用条件:
圆杆;
τmax≤τp。
其中极惯性矩和抗扭截面系数,在实心轴与非实心轴中的计算是不一样的。
在实心轴的情况下:
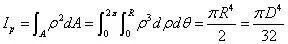
其中,D 为圆截面直径。
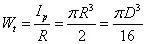

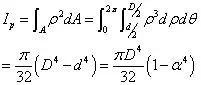
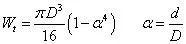
以上就是完整的求圆轴扭转时的应力的方法和过程了!
登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2021-06-08
最近编辑:3年前
还没有评论
相关推荐
最新文章
热门文章




