【技贴】工程应力应变、真实应力应变及修正应力应变!
一、屈服点比较明显的材料(如金属)
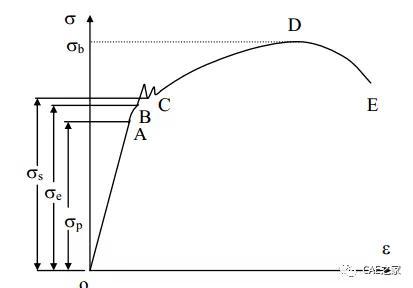
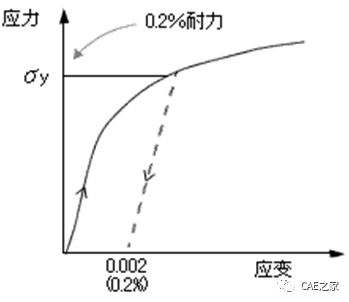
二、屈服点不明显的材料(如铜、铝及铸铁等)
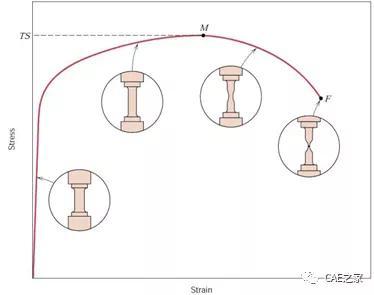
三、拉伸应力-应变曲线

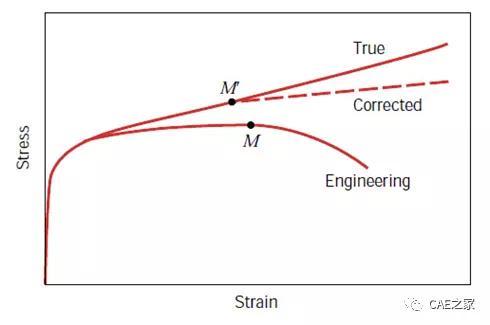
2、真实应力-应变曲线:是指在拉伸过程中,试样的截面积和长度随拉伸力的增大不断变化。
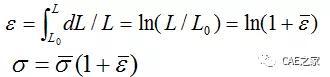
注:真实应变通常小于工程应变,且变形量愈大,两者差距也愈大;真实应力通常大于工程应力;
3、修正应力应变曲线:指在考虑结构缩颈后出现的不均匀变形,且不再是单应力状态,一般会出现加工硬化现象,此时应力会升高,需修正真实应力-应变曲线。
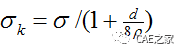
注:式中d为颈缩处试件直径;p为颈缩处试件外形的曲率半径。
四、CAE与理论计算结果对比
对于结构而言,其工程应力或名义应力计算公式如下:
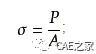
工程应变或名义应变:
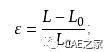
式中,P为外载荷;A为试样的初始横截面积;L0为试样的原始长度;L为试样变形后的长度。
案例:若某一试件,材料为钢,直径为20mm,长度为100mm,外力为1000N,如下所示。
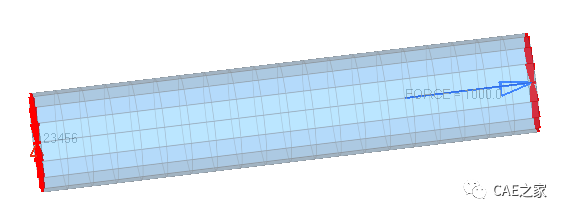
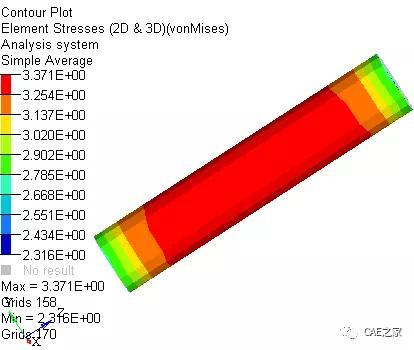
1、通过理论计算可得其工程应力约为3.183MPa,由CAE计算可得其Mises应力为3.371MPa,差异为5.9%;
2、理论计算值小于CAE值,其主要原因是理论计算时,假定横截面积不定;
3、而CAE计算时,在外力作用下,横截面积会变小,即应力会变大;
4、通过理论计算可验证CAE仿真结果的合理性,也验证了力学基础理论的重要性。
登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2021-06-02
最近编辑:3年前
作者推荐
还没有评论
相关推荐
最新文章
热门文章





