第1篇 带你进入结构有限元的世界
有限单元法,简称有限元,顾名思义,是将无限计算域划分成有限单元进行求解。其本质实际最终还是归结于数学求解问题,涉及基础学科包括高等数学、数值分析、线性代数、变分法等,结构工程专业学科包括理论力学、材料力学、弹性力学、动力学等。
很多读者对有限元存在天生恐惧感,原因大致归为两类,一、大部分有限元软件均为英文版本;二、有限元涉及的数学理论和力学理论较多,对于早已步入社会的读者而言,有种望尘莫及的感觉。作为本系列文章(共计15~20篇)的第1篇,笔者力争使用朴素易懂的语言带领大家认识有限元基础知识和Ansys软件操作过程,伴随笔者一步一步进入结构有限元的奇妙世界。
下面就以一个单向受拉构件的案例将有限元的计算思想使用简单的材料力学和线性代数展现给读者。
如图1,一根简直梁,左端可以自由旋转,但被限制X和Y轴平动,右端可以旋转,但被限制Y轴平动,同时右端受到一个X轴F=100N的轴向力,杆的长度为L=200mm,杆截面的面积为A=50mm2,弹性模量E=210000Mpa,求右端的X向位移。

图1
在介绍有限元知识之前,有必要与读者共同复习一下《材料力学》胡克定律:

公式1即为图1右端位移的解析解。公式1经过简单的移项可改写为公式2:
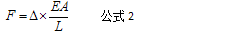
公式2中EA/L项即为单元刚度k。
下面开始推导有限元一维杆单元线性静力学典型方程,将图1轴向受拉构件划分成一个杆单元,杆单元分左右i、j两个节点,每个节点有一个自由度,即沿X方向的平动自由度,如图2:

图2
由图2可知,杆件左右两侧均受轴向力作用,左侧Fi和右侧Fj的内力可由公式2推导如下:
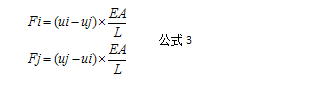
公式3写成矩阵形式,如公式4:

公式4中有ui与uj两个未知量,因此可知,若1个节点有1个广义位移未知量,1个一维杆单元包含两个节点,则1个单元共有两个广义位移未知量,最终构成的矩阵为2×2的方阵。
公式4可简写成公式5:

式中,

公式5即为有限元线性静力学的典型方程。
当然,公式4仅为1个单元的静力平衡方程,若将图1的轴向受力构件划分成两个单元,则需要将两个单元平衡方程进行组装。下面就以图1的构件为例,将其划分成两个单元,计算其右侧的轴向位移。
单元划分如图3,左侧定义为1号单元,右侧定义为2号单元,共有3个节点,3个未知位移,故最终构成的矩阵应该是3×3的方阵:

图3
1号单元的静力平衡方程如公式6:

2号单元的静力平衡方程如公式7:
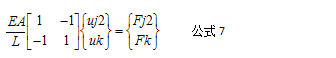
在组装矩阵之前,需要扩充公式6和公式7,扩充矩阵的目的是将3个节点的位移全部纳入到总刚矩阵中便于后面矩阵叠加,扩充后的公式6和公式7如下:

下面将扩充后的公式6和公式7合并、组装,如公式8:

若按公式8求解图1结构的位移将无法求解,因为式8中的总刚矩阵K的行列式为0,这将导致矩阵的奇异性,进而使式8变得无解或者有无穷解,正是由于此原因,初学者在使用有限元软件求解线性静力学问题时,若由于结构约束不足,软件会给出报错提示。
若让式8有解,需要对式8加入边界条件,本例的边界条件是左侧i节点的轴向位移为0,即ui=0是已知的,故将式8的第一行和第一列从矩阵中去除,式8变更为式9,如下式:
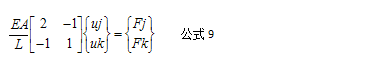
将其它已知条件(弹性模量E、杆长L、杆截面面积A及右侧集中力F)带入式9:
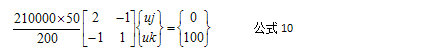
为方便初学者学习,将公式10从矩阵形式改写成线性方程组的形式:
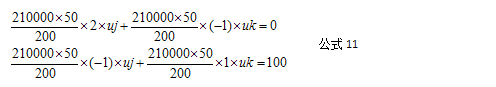
求解公式11,得:
ui=0mm uj=0.00095mm uk=0.0019mm
由结果可知,有限元方法求出的基本结果是位移,应变、应力场是基于位移基本解派生而出的。另外,本案例的结果仅求出了i,j,k三个节点的位移,杆中的其它部位的位移需要通过单元形函数求得,形函数的概念感兴趣的读者可自行查阅相关书籍。
通过以上一个简单案例,相信读者已对杆单元的线性静力学典型方程推导有了一定了解,值得注意的是,以上推导过程仅适用于杆单元结构,实体单元、壳单元由于其自身的结构特性,其典型方程需要采用变分法及最小势能原理推导。
第一时间获取文章内容可关注微信公众号“机械人读书笔记”。




