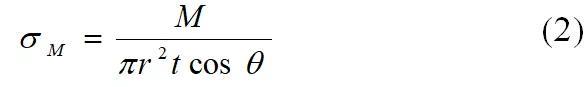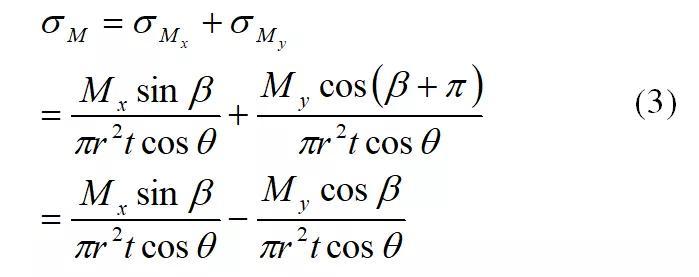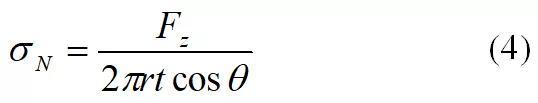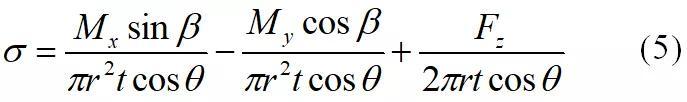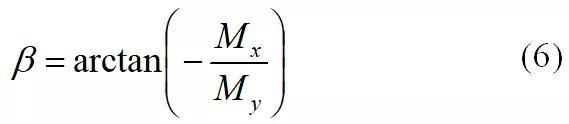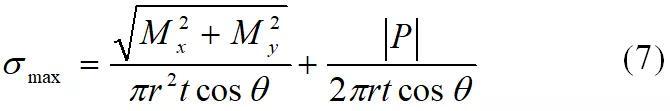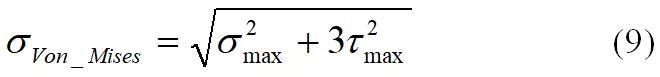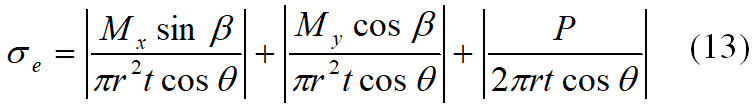大型水平轴风力机塔筒焊缝强度分析（文末附直播）

详细信息

作者优秀: 优秀教师/意见领袖/博士学历/特邀专家/独家讲师
平台推荐: 主编推荐

3年前浏览3449

导读：为实现某大型水平轴风力机塔筒截面焊缝强度设计，介绍了DIN18800-4应力计算的工程算法，针对2.0 MW直驱型风力机塔筒某一截面进行极限强度校核。根据疲劳载荷分类，提出等效疲劳损伤和时序疲劳损伤两种不同计算方法。推导了等效疲劳载荷、等效疲劳应力与等效疲劳损伤的计算公式。针对某一截面进行等效疲劳损伤和时序疲劳损伤分析计算和结果对比，给出两者等价性条件与适用条件。结果表明，被校核的截面焊缝满足强度设计要求。提出的方法在大型水平轴风力机塔筒截面焊缝极限强度与疲劳强度分析上具有可行性和有效性。

点击上图可观看

一、写在前面

近年来，随着风力发电机向大型化趋势发展，结构零部件面临着更加严苛的工作环境，结构强度问题尤其是抗疲劳设计方法已日益得到国内外研究者的重视。

李德源等[1]较早介绍了玻璃钢材料的疲劳破坏过程及破坏准则，探讨了玻璃钢材料疲劳性能及疲劳寿命估计方法。
傅程等[2]以刚度退化模型为基础，发展了适合风力机叶片的损伤演化模型，模拟了某叶片的真实疲劳试验过程。
姚兴佳等[3]采用ANSYS有限元分析软件计算校核了机舱底盘的静强度，并提出结构改进方案。
陈严等[4]利用叶素动量理论得到轮毂动态载荷极限值和叶根处的动态载荷，提出水平轴风力发电机组轮毂的强度分析方法，并介绍了轮毂与叶片连接螺栓的强度分析方法。
刘建军等[5]提出一种新型桁架式海上风电支撑结构，并应用有限元法分析研究了其静动态特性。

大型水平轴风力机塔架大致可分为钢筋混凝土、桁架及钢筒3种结构形式。其中，圆锥筒形薄壁塔筒得到较广泛的应用。

在塔筒结构强度研究方面：

李德源等[6，7]研究了海上风力机塔筒在随机风载荷和波浪载荷作用下的动力响应数值分析方法，建立了基于Palmgren Miner线性累计损伤法则的混泥土塔架安全寿命估计方法。
陈严等[8]考虑三维紊流风场、Beddoes-Leishman动态失速模型、惯性载荷及重力载荷计算了风力机整机载荷，并对水平轴风力发电机组的塔架静态强度、动态屈曲、模态特性进行了研究。
刘雄等[9]利用二结点梁单元得到塔架的离散化模型，分析了弯曲振动固有特性和湍流风条件下的动态响应。

本文介绍了DIN18800-4塔筒截面焊缝应力计算的工程算法。针对某一高度塔筒截面焊缝，分析校核了其极限强度。根据疲劳载荷分类，提出了等效疲劳损伤和时序疲劳损伤两种不同计算方法，推导得到等效疲劳应力、等效疲劳损伤的计算公式。应用两种不同疲劳分析方法计算得到截面焊缝不同位置处的累积损伤值。通过数值算例考察了单一载荷、多载荷联合作用下的计算结果，通过对比分析，指出了两种方法的适用性。

二、塔筒截面应力计算方法

由于塔筒薄壁截面受周向应力较小，本文仅考虑薄壁圆筒截面的正应力和剪应力，正应力由弯矩和轴向载荷引起，剪应力由扭矩和剪切力引起。塔筒的截面应力计算分为有限元法和工程算法两类方法，除去塔筒底部门洞和顶部法兰段外，塔筒由薄壁圆筒件焊接而成，结构形式上满足材料力学的基本假设，可采用材料力学应力计算公式得到其截面应力值，但材料力学方法忽略了塔筒锥度。为考虑塔筒锥度，这里采用了DIN18800-4中的应力计算方法。

设塔筒各段锥角相等，其数学表达式为：

式中，Dbottom——塔筒底部直径；Dtop——塔筒顶部直径；H——塔筒高度。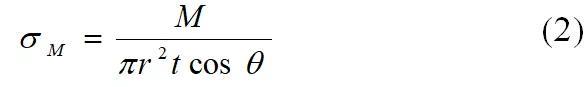

截面弯矩引起的最大正应力数学表达式为：

式中，M——截面弯矩；r——薄壁圆筒的中径；t——塔筒壁厚。将M分解为Mx和My两个方向的弯矩，如图1所示，塔筒截面应力随角度的变化而变化，弯矩引起的正应力数学表达式为：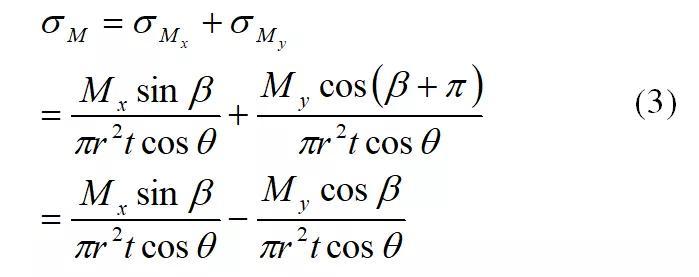

式中， ——塔筒截面任意位置与x轴夹角，图1中的坐标系符合GL2010规范中的塔筒底部坐标系定义。

图1 塔筒截面坐标系

Fig. 1 Coordinate system for the tower section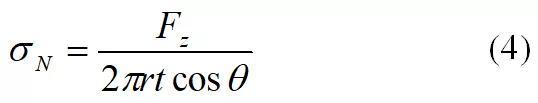

塔筒轴向载荷引起的正应力数学表达式为：

式中，Fz——截面轴向载荷。

故而塔筒截面正应力由Mx、My和Fz三部分引起，根据式(3)～(4)可得合成正应力表达式为：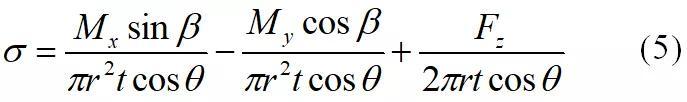

对式(5)求导并令其值为零，可得到正应力极值对应的角度为：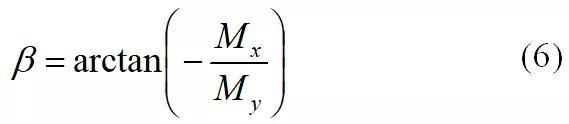

由于截面轴向载荷Fz主要由重力引起，其方向为z向反向，即轴向正应力数值上为负数，故而截面正应力绝对值最大的数学表达式为：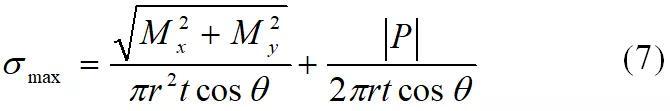

同理，根据DIN18800-4工程算法，可得截面剪应力绝对值最大的数学表达式为：

尽管正应力最大值与剪应力最大值发生位置并不一致，为简单起见，可直接将两者进行合成叠加，根据材料力学第四强度理论，等效应力最大值表达式为：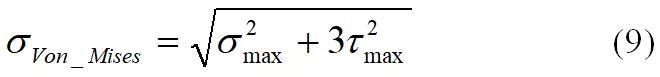

三、塔筒焊缝极限强度分析

本节选取某一塔筒截面焊缝进行数值分析，所采用的几何数据包括：截面外径4.2 m，薄壁厚度32 mm，塔筒高度72.37 m，塔筒顶部与底部直径差1.8 m。塔筒薄壁圆筒采用Q345钢，由于材料屈服强度值随薄壁厚度增加而减小，这里取屈服强度值为325 MPa，材料局部安全系数为1.15。根据GL2010认证规范，由Focus软件输出塔筒段截面中心处的载荷值，共14个极限工况和70个疲劳工况，每个工况包括3个方向的力和3个方向的矩。以Fx_min工况为例，该工况表示在所有的载荷工况中，x方向力的代数值最小对应的工况，其他工况的含义依此类推。塔筒截面焊缝极限工况分析结果如表1所示。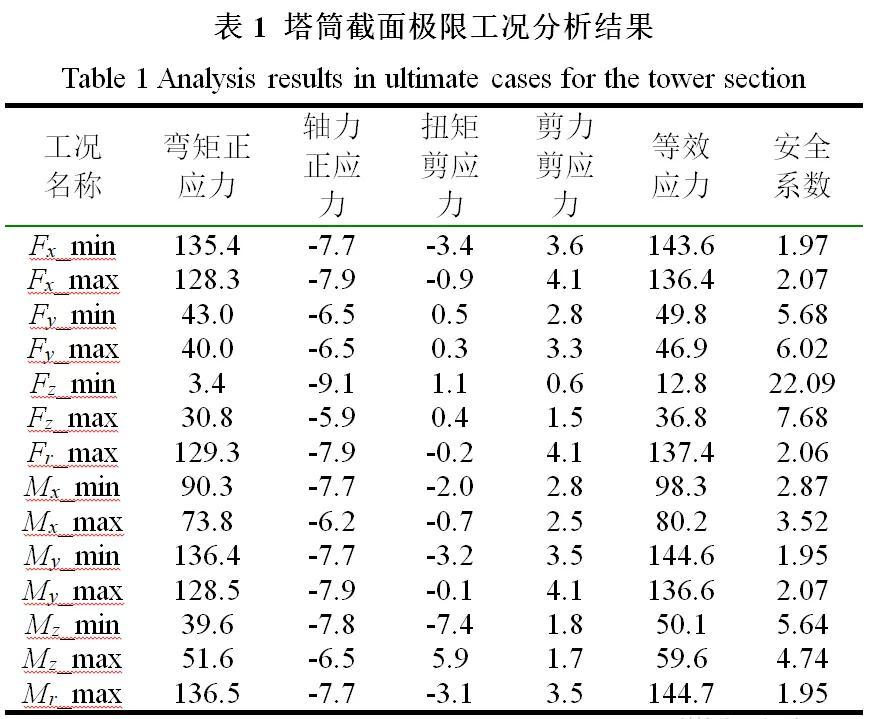

由表1可知，在大多数极限工况内，弯矩正应力值远大于其他应力分量值，说明较大的弯矩值是引起工况危险的主要原因。工况Mr_max为最危险工况，等效应力值与安全系数分别对应为144.7 MPa和1.95，故而结构设计满足极限强度要求。

四、塔筒焊缝疲劳强度分析

1、焊缝疲劳分析方法与流程

由上节极限强度分析结果可知，塔筒截面焊缝的极限强度具有一定的冗余度。由于风电零部件设计通常需满足20年抗疲劳设计要求，故而除了极限强度校核外，仍需对塔筒截面焊缝进行疲劳强度校核。

根据GL2010认证规范，风力机疲劳载荷计算结果包括时序疲劳载荷和等效疲劳载荷(damage equivalent loads，DEL)两种。根据疲劳载荷的分类，这里提出等效疲劳强度分析和时序疲劳强度分析两种不同方法。

对于等效疲劳强度分析方法而言，首先对时序疲劳载荷进行雨流计数，然后计算等效疲劳载荷（幅值），从而计算得到等效疲劳应力（幅值）与等效疲劳损伤。而对于时序疲劳强度分析，需首先计算截面某角度对应的时序疲劳应力，然后对时序疲劳应力进行雨流计数和累计损伤计算。上述两种方法对应的流程如图2所示。

图2 焊缝疲劳强度分析流程

Fig. 2 The flowchart for the fatigue analysis on weld

由上节极限强度分析结果可知，截面剪应力在合成应力中所占比例较小，在焊缝疲劳分析中，若考虑剪应力将涉及到疲劳多轴性问题，为简化起见，以下疲劳分析仅考虑正应力作用。

2、焊缝材料S-N曲线

根据GL2010规范，推荐的常用S-N曲线包括Eurcode3和IIW两种形式，两者均由指数斜率分别为 3和5的两线段组成，所不同之处在于线段拐点分别对应次数为5×10^6和1×10^7。如图3所示，通常标准设计S-N曲线均指出结构在2×10^6次循环下的特定疲劳强度，并定义为疲劳级别(detail category，DC)，如DC为90的S-N曲线表示其在2×10^6次循环下，以应力幅值表征的疲劳强度为90 MPa。本文选择Erucode3标准做为塔筒焊缝材料S-N曲线的基本形式，DC等级选择为90。通常情况下，对于焊缝材料不考虑平均应力对疲劳损伤的影响，故而这里不再进行Goodman修正。

图3 焊缝材料的S-N曲线

Fig. 3 S-N curve for weld material

由图3可知，可通过S-N曲线与DC值推导S-N曲线上任意次数处的应力幅值。例如求如图3中C点对应的应力幅值，可由A点计算得到B点处对应的应力幅值，然后再计算得到C点处对应的应力幅值，其数学表达式为:

式中，m1，m2——分别代表指数斜率值，这里取m1=3，m1=5。

3、等效疲劳强度分析

等效疲劳载荷（幅值）Le定义为：

式中，Li——时序疲劳载荷雨流计数得到的载荷幅值；Ni——对应的循环次数；m——等效疲劳载荷指数斜率。由于风电结构零部件采用20年设计寿命，即对应循环次数为1×10^7，这里NC=1×10^7。根据上述计算公式，可得到如表2所示的不同m值下的等效疲劳载荷结果。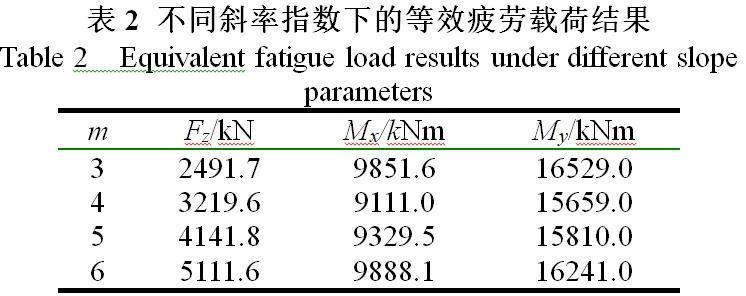

由于图3中次数1×10^7处对应的指数斜率值m2为5，为保持一致性，这里可取表2中m=5对应的等效疲劳载荷值，将该值代入到应力计算公式中，即可得到等效疲劳应力（幅值）结果。由于等效疲劳载荷为雨流计数结果，需根据式(5)对等效疲劳应力公式略作修改，例如当仅Mx载荷作用时，等效疲劳应力表达式为：

而针对多种载荷联合作用的情况，等效疲劳应力数学表达式为：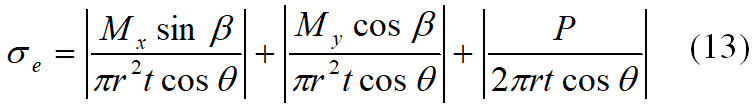

假设结构在等效疲劳应力作用下，可经历的循环次数为Ne，则有：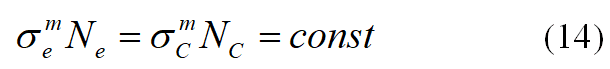

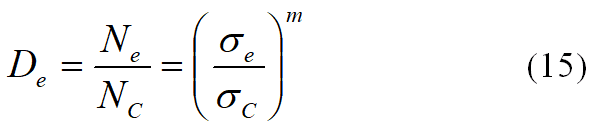
根据损伤定义得到等效疲劳损伤表达式为：

根据上述推导可知，式(14)是等效疲劳损伤成立的前提，即需满足相同参数下的S-N曲线方程，时序疲劳应力雨流计数的幅值应小于图3所示B点对应的应力幅值。

2、数值算例分析结果

1) 仅考虑单载荷作用的疲劳强度分析结果对比

不失一般性，这里仅考虑弯矩Mx作用下，两种不同疲劳损伤计算结果进行对比。由于应力幅值具有截面对称性，这里从0o～90o每隔30o，计算得到如表3所示的疲劳损伤结果。

显而易见，当弯矩Mx作用时，应力绝对值最大点发生在或处。由表3可知，等效疲劳损伤与时序疲劳损伤值接近。这是由于弯矩引起的正应力值与弯矩值呈正比，等效疲劳损伤与时序疲劳损伤计算的区别仅是由于雨流计数对象不同而已，两者之间的差别除却数值舍入误差外，还包括个别工况下的应力幅值超过了图3中拐点B对应的应力幅值所致，由于这部分应力幅值所占比例较小，故而等效疲劳与时序疲劳损伤结果接近，这一点在两者之间的相对误差中也有所体现。

同理可得到如表4所示的My作用下等效疲劳损伤与时序疲劳损伤对比。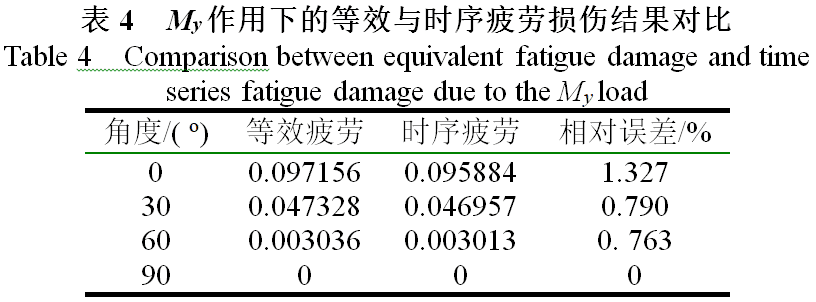

将上述结果绘制于图形中，得到如图4所示的等效疲劳损伤与时序疲劳损伤截面分布雷达图。

a. Mx单独作用

b. My单独作用

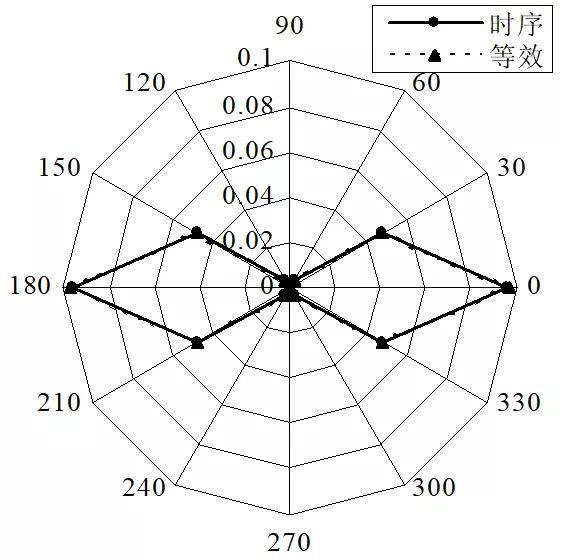
图4 等效疲劳损伤与时序疲劳损伤对比

Fig. 4 Comparison between the equivalent fatigue damage and time series fatigue damage

由图4可得，My单独作用下的等效与时序疲劳损伤值规律与Mx单独作用下一致，即两种疲劳分析方法具有等价性。

2) Mx和My联合作用的疲劳强度分析结果对比

这里以截面角度30o和150o为例，得到如表5所示的Mx和My联合作用下疲劳强度分析结果对比。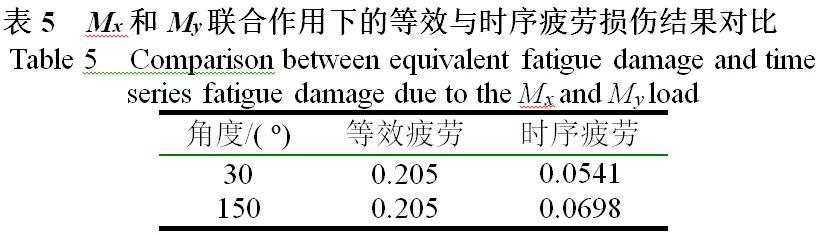

由表5可知，30o和150o两个不同位置的时序疲劳损伤值不同，这是由于两个不同位置处的时序应力幅值完全不同。而等效疲劳损伤计算方法无法辨别不同角度下的损伤结果。这是由于在等效疲劳损伤计算流程中，时序载荷被用于雨流计数，等效载荷（幅值）具有恒大于零的特性，从而在等效疲劳应力计算中，无法辨别角度引起的正负性。在时序疲劳应力计算中，能充分考虑到时序应力的符号性和随截面角度不同而不同的特点，故而能得到正确的疲劳损伤结果。

3) Mx、My和Fz联合作用的疲劳强度分析结果

基于上述分析结论，在考虑Mx，My和Fz联合作用时，采用时序疲劳损伤计算方法，每隔30o，得到如图5所示的随角度变化的疲劳损伤分布。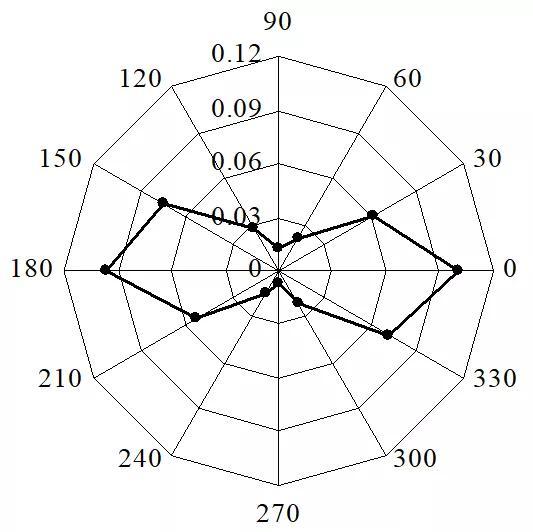

图5 疲劳损伤分布

Fig. 5 Distribution of the fatigue damage

由图5可知，最大损伤出现在 o之间的区域，近似在0o附近。为进一步得到较精确的结果，可细分0o附近区域进行重新计算，得到如图6所示的疲劳损伤分布。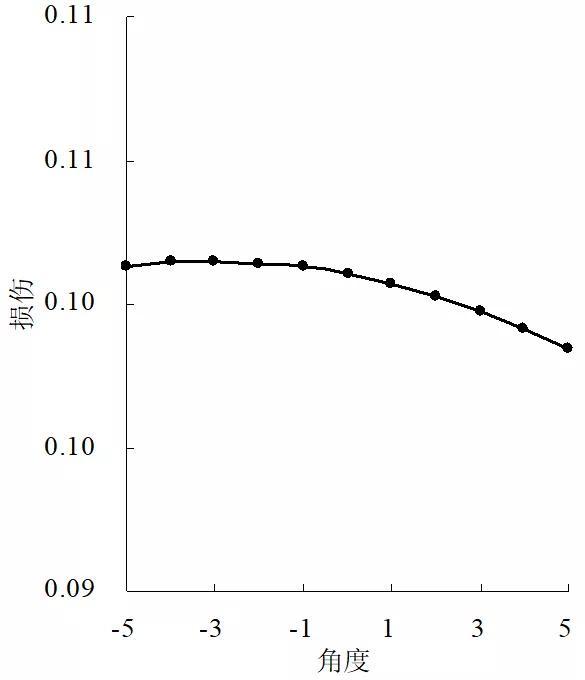

图6 疲劳损伤分布

Fig. 5 Distribution of the fatigue damage

由图6可知，疲劳累积损伤在0o附近呈不对称分布，最大损伤点约发生在-3o处，其累计损伤值为0.101 49（这是一个数值还是两个？一个，即0.10149），由于数值小于0.5，故而满足疲劳强度设计研究。

五、结论

本文研究了大型水平轴风力机塔筒截面焊缝的强度分析方法。采用 DIN18800-4工程算法计算得到塔筒截面焊缝应力，校核了某一截面焊缝的极限强度。根据疲劳载荷分类，提出等效疲劳和时序疲劳损伤两种不同计算方法。推导了等效疲劳载荷、等效疲劳应力与等效疲劳损伤计算公式。针对某2MW直驱型风力机截面焊缝，分析对比了不同情况下等效疲劳和时序疲劳损伤结果。结果表明结构设计满足强度设计要求。本文提出的分析方法可作为一种实用的大型风力机塔筒焊缝强度分析与设计手段。考虑到截面焊缝应力的复杂性，应力多轴性对疲劳损伤结果的影响仍有待进一步讨论。

[参考文献]

[1]李德源，叶枝全，陈严，等. 风力机玻璃钢叶片疲劳寿命分析[J]. 太阳能学报，2004，25(5)：592—598.
[1]Li Deyuan, Ye Zhiquan, Chen Yan, et al. Fatigue life analysis of the glass reinforced plastic bladed of horizontal axis wind turbine[J]. Acta Energiae Solaris Sinica, 2004, 25(5): 592—598.
[2]傅程，王延荣. 风力机叶片损伤演化模拟[J]. 太阳能学报，2011，32(1)：143—148.
[2]Fu cheng, Wang Yanrong. Damage evolution prediction of wind turbine blades[J]. Acta Energiae Solaris Sinica, 2011, 32(1): 143—148.
[3]姚兴佳，张晨晨，单光坤，等. 基于ANSYS的风力发电机机舱底盘的强度分析[J]. 沈阳工业大学学报，2008，30（1）：38—41.
[3]Yao Xingjia, Zhang Chenchen, Shan Guangkun, et al. Strength analysis of wind turbine nacelle chassis based on ANSYS[J]. Journal of Shenyang University Technology, 2008, 30(1): 38—41.
[4]陈严，田鹏，刘雄，等. 水平轴风力机轮毂强度分析方法研究[J]. 太阳能学报，2010，31(7)：912—916.
[4]Chen Yan, Tian Peng, Liu Xiong, et al. Research on strength calculation methods of rotor hub of HAWTs[J]. Acta Energiae Solaris Sinica, 2010, 31(7): 912—916.
[5]刘建军，黄维平. 新型海上风电支撑结构设计与分析[J]. 太阳能学报，2011，32(11)：1616—1621.
[5]Liu Jianjun, Huang Weiping. The design and analysis of the new type support structure of offshore wind turbine[J]. Acta Energiae Solaris Sinica, 2011, 32(11): 1616—1621.
[6]刘胜祥，李德源，黄小华. 风波联合作用下的风力机塔架疲劳特性分析[J] . 太阳能学报，2009，30(10)：1250—1256.
[6]Liu Shengxiang, Li Deyuan, Huang Xiaohua. Fatigue characteristic analysis of the offshore wind turbine tower under combined wind and wave[J]. ACTA ENERGIAE SOLARIS SINICA, 2009, 30(10): 1359—1365.
[7]李德源，刘胜祥，张湘伟. 海上风力机塔架在风波联合作用下的动力响应数值分析[J]. 机械工程学报，2009，45(12)：46—52.
[7]Li Deyuan, Liu Shengxiang, Zhang Xiangwei. Dynamical response numerical analysis of the offshore wind turbine tower under combined action of wind and wave[J]. Journal of Mechanical Engineering, 2009, 45(12): 46—52.
[8]陈严，田鹏，刘雄，等. 水平轴风力机锥形塔筒的静动态特性研究[J] . 太阳能学报，2010，31(10)：1359—1365.
[8]Chen Yan, Tian Peng, Liu Xiong, et al. Research on static and dynamic characteristics of cone-shaped tower of HAWTs[J]. Acta Energiae Solaris Sinica, 2010, 31(10): 1359—1365.
[9]刘雄，李钢强，陈严，等. 水平轴风力机筒形塔架动态响应分析[J]. 太阳能学报，2010，31(4)：412—417.
[9]Liu Xiong, Li Gangqiang, Chen Yan, et al. Dynamic response analysis of the tubular tower of horizontal axis wind turbines[J]. Acta Energiae Solaris Sinica, 2010, 31(4): 412—417.

六、写在后面

2020年8月，笔者在仿真秀原创的精品课《大型风电机组零部件疲劳强度分析》已经全部上架，深受用户喜爱。5月26日20时受平台邀请为订阅用户带来微小课《基于梁单元的风电塔筒叶片建模》加餐直播，即日起到直播开始前开通免费报名，欢迎分享和订阅。更多内容请在仿真秀官网和APP搜索大龙或点击文章末尾的阅读原文关注我的专栏。我的免费课程《计算机辅助工程》、《可靠性工程》和《机械振动课程》給大家长期免费开放。

以下是我的直播安排（点击下图可观看）