NVH那些事(十一)
说了激振力,又说了系统的固有特性,接下来就说说一个振动系统在激振力的作用下,会产生怎样的振动响应。这和一个电路在电源激励下会产生电流响应类似,因此在解析法分析振动问题时,往往参照电路的解析方法进行解算。1 振动系统与电路系统的类比
1.1 电路系统的数学模型
在电路系统中,有三种基本元件,即电阻R、电感L和电容C,它们的特性分别为:对于电阻u=R•i;对于电感u=L•di/dt;对于电容u=(1/C)•∫i•dt,其中u为电压;i为电流。如果把一个电阻、电感和电容串联起来就组成一个RLC串联电路,如图1所示。

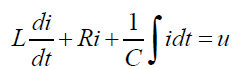 (1)
(1)
由于电路中的电量Q=∫i•dt,将其代入⑴式,则该电路的数学模型也可以用电量Q作为变量来表示:
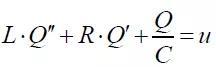 (2)
(2)
1.2 平移振动系统的数学模型
平移振动系统中同样存在三种基本元件,即阻尼rm、质量m和弹性元件λm(λm为弹性元件的柔度,即刚度的倒数),它们的特性分别为:阻尼力f=rm•v;惯性力f=m•dv/dt;对于弹性元件的弹性力f=(1/λm)•∫v•dt,其中v为运动速度。那么对于一个如图2所示的一阶平移振动系统,其运动方程(数学模型)即为:
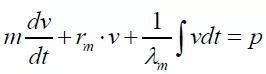 (3)
(3)
由于振动位移x=∫ v•dt,则⑶式也可以变为用位移x作为变量来表示其运动方程:
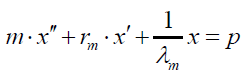 (4)
(4)
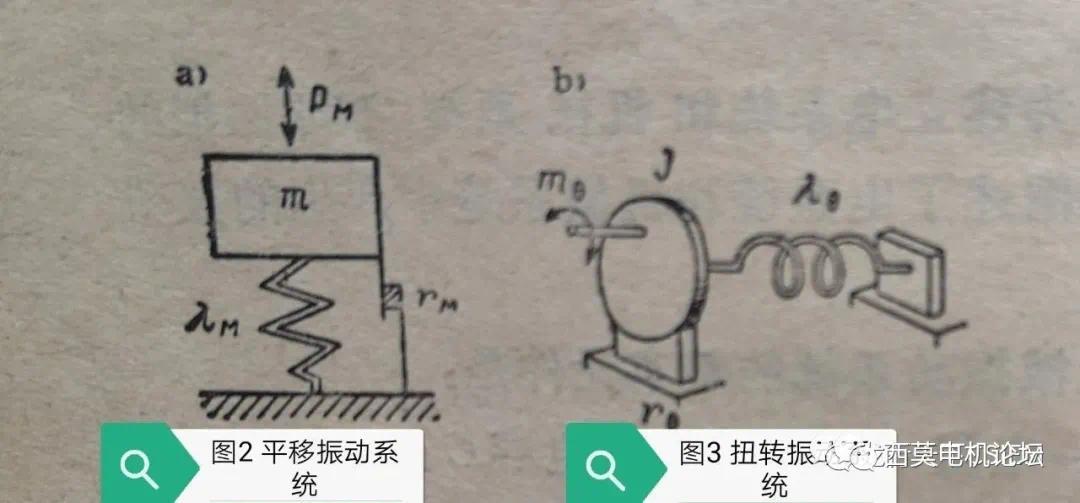
1.3 扭转振动系统的数学模型
同理对于一个如图3所示的一阶扭转振动系统,其运动方程(数学模型)为:
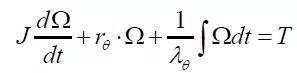 (5)
(5)
其中:J为转动惯量;rθ为扭转阻尼系数;λθ为扭转刚度;Ω为扭转角速度;T为扭矩。由于扭转角位移φ=∫ Ω•dt,则⑸式也可以变为用角位移φ作为变量来表示其运动方程:
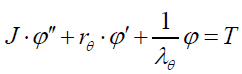 (6)
(6)
1.4 振动系统与电路系统的类比
通过以上类比,我们可以清楚地看到,一个机械振动系统的数学模型和一个电路振荡系统的数学模型是相同的,这就是通常说的这个世界是大同小异的,但其本质是相通的。在固有参数方面:振动系统的阻尼就相当于电路系统的电阻;振动系统的柔度相当于电路系统的电容;而振动系统的惯量(质量或转动惯量)就相当于电路系统的电感。在状态参数方面:振动系统的位移(线性位移或角位移)就相当于电路系统的电(荷)量;振动系统的速度(线性速度或角速度)就相当于电路系统的电流。在激励源方面:振动系统的激振力(或激振扭矩)就相当于电路系统的电压。
2 交变激励下系统的稳态响应
建立了上述电路系统和振动系统的数学模型,我们就可以通过解算上述三个微分方程(2)、(4)、(6)来得到电路系统和振动系统在激振力的作用下产生的电路状态和振动状态响应(解算过程详见科学瞎想系列之六十),由于解算过程极其复杂,这里不做过多的数学推导,重点讲最终结果。值得一提的是,上述三个微分方程的解必然与系统的初始状态有关,也就是说,得到的响应结果应该是由暂态分量和稳态分量组成,考虑到由于系统中存在阻尼,暂态分量会随着时间推移而逐步衰减到0,最终只剩下稳态分量,即受迫振动分量,这里只说最终稳态响应结果。
2.1 电路系统的响应
对于图1所示的电路系统,如果激励源为正弦变化的电压,即u=Um•sinωt,根据正弦交流电路的有关理论,在稳态下电路中的电压、电流等状态物理量可以用相量来表示,那么在稳态下,上述电路的电流相量为:
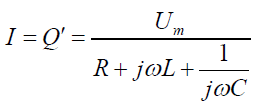 (7)
(7)
2.2 平移振动系统的响应
对于图2所示的平移振动系统,如果激励为正弦变化的激振力,即p=Pm•sinωt,那么可以参照正弦交流电路的分析方法,在稳态下系统的振动速度为:
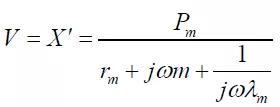 (8)
(8)
2.3 扭振振动系统的响应
对于图3所示的扭转振动系统,如果激励为正弦变化的激振力矩,即T=Tm•sinωt,同样可以参照正弦交流电路的分析方法,在稳态下系统的振动角速度为:
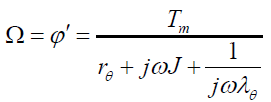 (9)
(9)
以上类比分析可见,对于一个机械振动系统,其振动的响应与一个电路系统的数学模型是相同的,因此我们可以按照电路系统的解算方法去解算机械振动系统的响应。在正弦交流电路系统中,电流响应与激励电压之间的关系符合欧姆定律,即电流等于电压除以电路的复数阻抗(或电压乘以电路的复数导纳),同理机械振动系统的振动速度(或角速度)与激振力(或力矩)之间的关系同样符合欧姆定律,这里不妨引入一个机械振动系统的基本概念,即复数机械阻抗(或复数机械导纳),上述式⑻、⑼中的分母部分即为机械振动系统的复数阻抗,其倒数即为复数导纳。这样对于一个机械振动系统的解算即可归结为复数阻抗或导纳的分析确定。
3 常见电机振动系统的解析
3.1 安装于双层隔振装置的电机系统的机械阻抗
如图4a为电机安装在双层隔振装置上组成的振动系统,电机的质量为m1,其底脚下面的第一级隔振器的柔度为λ1,再下面是第二级隔振装置,其质量为m2,第二级隔振器柔度为λ2,电机的激振力为p0。该系统的简化模型为图4b,比拟的电路系统为图4c。
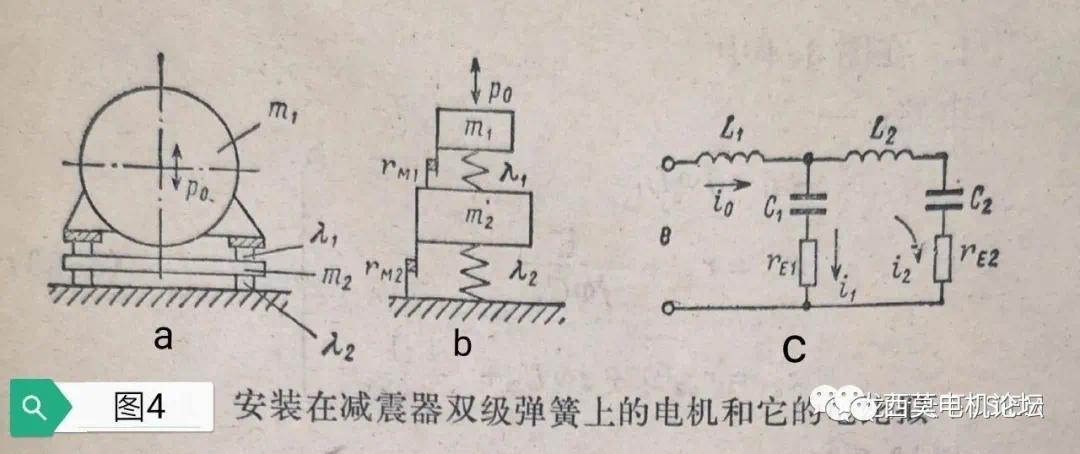
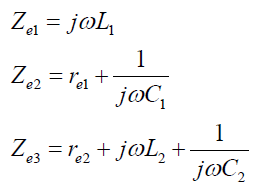 (10)
(10)
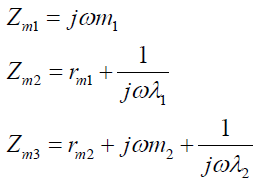 (11)
(11)
3.2 具有动力减震装置的电机系统的机械阻抗
如图5a为质量为m1电机安装在柔度为λ1的减震器上,同时在电机上面安装有质量为m2柔度为λ2的动力振动吸收器,激振力由中间的电机产生。后面的瞎想我们会讲到,安装动力振动吸收器是一种常见的减震措施,另外有些电机通过弹性减震器将冷却室、出线盒或其他附属部件安装于电机顶部,也同样起到了振动吸收作用,也相当于这种系统模型。该系统的简化模型为图5b,比拟的电路系统为图5c。
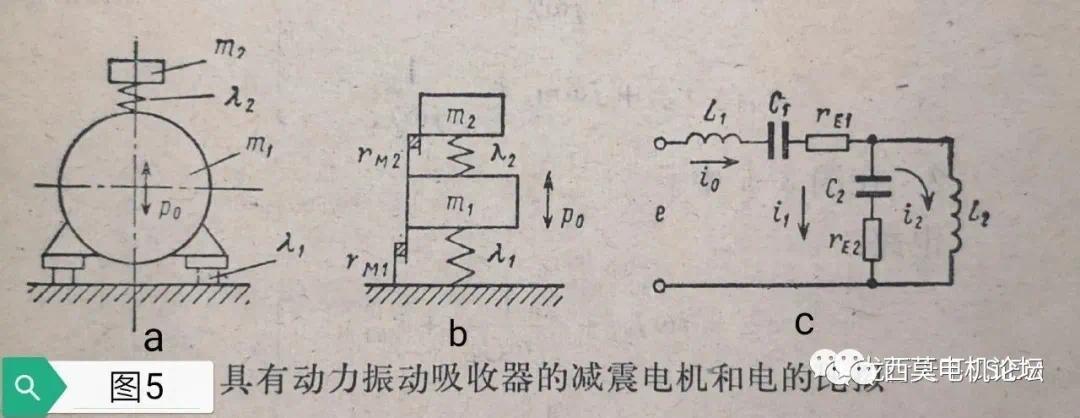
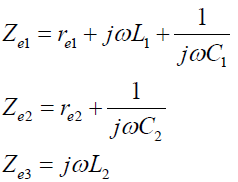 (12)
(12)
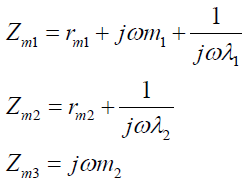 (13)
(13)
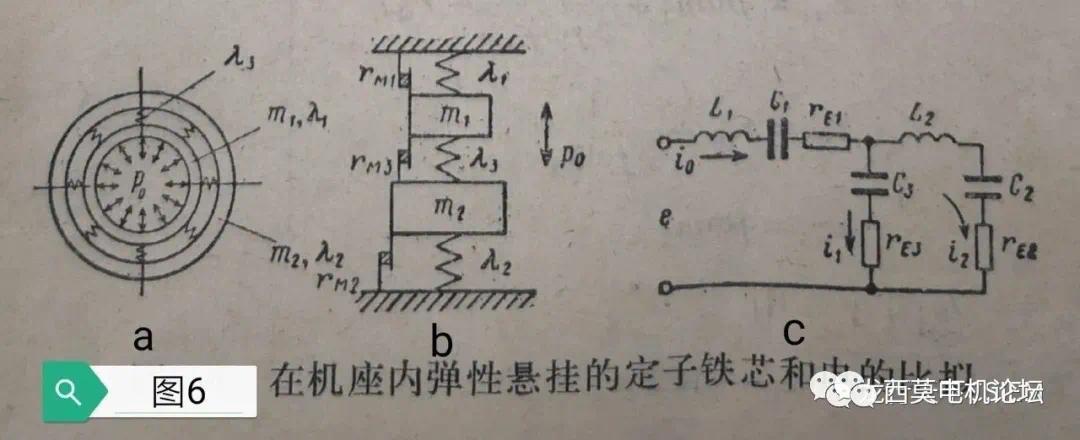
3.3 机座内弹性悬挂定子铁心组成的电机振动系统的机械阻抗
如图6a为质量为m1、柔度为λ1的定子铁心被弹性悬挂在质量为m2、柔度为λ2的机座内,悬挂弹簧的柔度为λ3,铁心由径向力波激振。这是一种最常见的电机振动系统,特别是大中型箱式电机都属于这种模型。该系统的简化模型为图6b,比拟的电路系统为图6c。
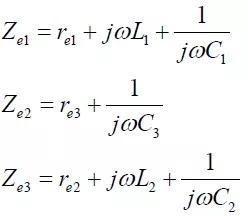 (14)
(14)
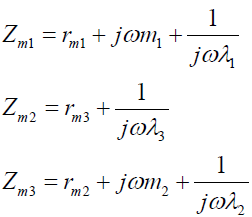 (15)
(15)
3.4 上述三种典型电机振动系统的解算
上述三种典型系统的比拟电路模型中,解算出的电流响应结果均为:
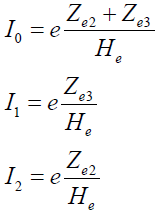 (16)
(16)
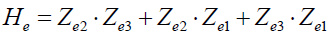 (17)
(17)
前面说过,在机械振动系统与电路系统类比时,振动速度就相当于电路中的电流,因此相应地电机系统各处的振动速度为:
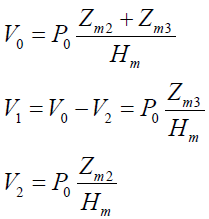 (18)
(18)
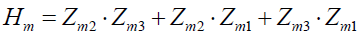 (19)
(19)
对于图4系统,这三个振动速度V0为电机m1的振动速度;V2为二级减震装置m2的振动速度;V1为一级减震器λ1两端的速度差。对于图5系统,这三个振动速度V0为电机m1的振动速度;V2为动力减震器m2的振动速度;V1为动力减震器λ2两端的速度差。对于图6系统,这三个振动速度V0为电机铁心m1的振动速度;V2为机座m2的振动速度;V1为震弹簧λ3两端的速度差。
4 振动系统分析的解析法小结
以上介绍了电机振动系统的解析方法,一个振动系统可以用一个电路系统来比拟,电路系统的电阻、电感和电容元件可以比作机械振动系统的阻尼元件、惯性元件和弹性元件;相应地电路系统中的阻抗就可以比作机械振动系统的机械阻抗;电路系统中的激励源(电压)可以比作机械振动系统的激振力或力矩;电路系统中的电流响应可以比作机械振动系统的振动速度或角速度。经过这样比拟后,机械振动系统的解析就可以按照电路的解析计算方法进行。需要再次强调的是,上述解析方法只是从理论和原理上给出的一种分析方法,这种方法概念很清楚,逻辑层次分明,不失为一种定性分析振动问题的好方法,但这种方法说起来容易,做起来难,比如确定机械元件的参数、确定激振力的大小等都不是一件很不容易的事情,一个特定的机械元件的参数可能还比较容易获得,但一个电机或电机零部件的惯性参数和柔度参数,特别是对于高阶振型的惯性分布参数和柔度分布参数,通常是很难准确获得的。因此这种方法只是在早期计算机仿真技术不够发达的时代常被采用,计算精度不高,只能反映一个数量级的结果,但由于该方法原理清晰,逻辑分明,在分析振动问题时可以给出宏观的理论指导和解决问题的方向,在当今计算机仿真技术发达的今天,要想精确计算电机振动值,还是建议采用专业的计算机仿真软件进行精确计算。

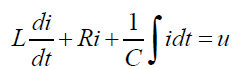 (1)
(1)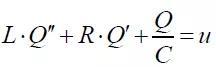 (2)
(2)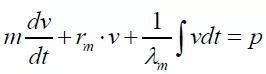 (3)
(3)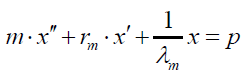 (4)
(4)
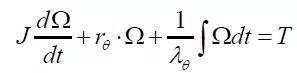 (5)
(5)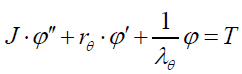 (6)
(6)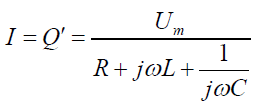 (7)
(7)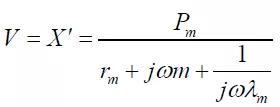 (8)
(8)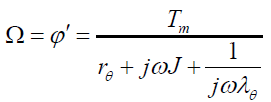 (9)
(9)
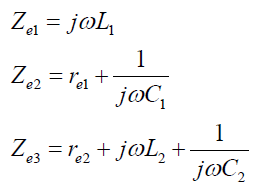 (10)
(10)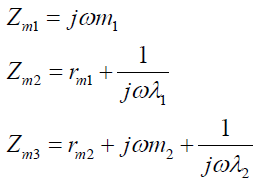 (11)
(11)
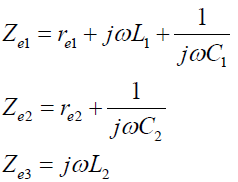 (12)
(12)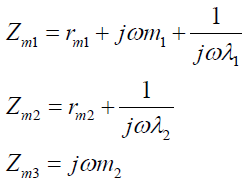 (13)
(13)
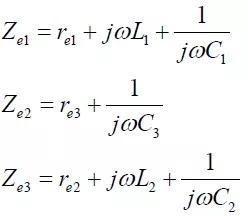 (14)
(14)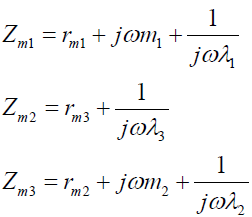 (15)
(15)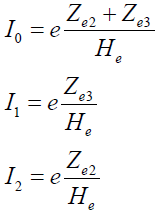 (16)
(16)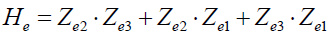 (17)
(17)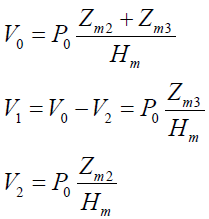 (18)
(18)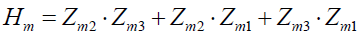 (19)
(19)




