首页/文章/ 详情

为什么是“50欧姆”？

射频学堂

1年前浏览2947

小木匠说：万万没想到，这个居然成了《射频学堂》第一篇阅读量过万的文章。足以看出基础知识对大家有多重要！！！（留图纪念，有图有真相），下个目标是，阅读量过十万。

这篇介绍50 Ohm作为标准阻抗的文章，最初发表于2020-6-11，作为一篇介绍射频基础知识的文章，归类到了“射频工程师必知必会”系列。我们今天重新编辑整理，希望能够呈现给大家更好的阅读感。

在射频设计中，我们经常会遇到一个特殊的阻抗值——50 Ohm。为什么标准阻抗值是50 Ohm，而不是其他的数值呢？可能很多人都有这个疑惑。实际上最常用的标准阻抗除了50 Ohm之外，还有个75 Ohm。

带着这个疑惑我们一起来探探究竟！

这里面既有历史因素，也有应用因素。

在Harmon Banning 的《电缆：关于 50 Ohm的来历可能有很多故事》一文中，详细介绍了关于50 Ohm标准阻抗的来历：在微波应用的初期，二次世界大战期间，阻抗的选择完全依赖于使用的需要，对于大功率的处理，30 Ohm和 44 Ohm常被使用。另一方面，最低损耗的空气填充线的阻抗是 93 Ohm。在那些岁月里，对于很少用的更高频率，没有易弯曲的软电缆，仅仅是填充空气介质的刚性导管。半刚性电缆诞生于 50 年代早期，真正的微波软电缆出现是大约 10 年以后了。随着技术的进步，需要给出阻抗标准，以便在经济性和方便性上取得平衡。在美国，50 Ohm是一个折中的选择；为联合陆军和海军解决这些问题，一个名为 JAN 的组织成立了，就是后来的 DESC，由 MIL 特别发展的。当时欧洲选择了 60 Ohm。事实上，在美国最多使用的导管是由现有的标尺竿和水管连接成的，51.5 Ohm是十分常见的。看到和用到 50 Ohm到 51.5 Ohm的适配器/转换器，感觉很奇怪的。最终 50 Ohm 胜出了，并且特别的导管被制造出来（也可能是装修工人略微改变了他们管子的直径）。不久以后，在 Hewlett-Packard （惠普）这样在业界占统治地位的公司的影响下，欧洲人也被迫改变了。75 Ohm是远程通讯的标准，由于是介质填充线，在 77 Ohm获得最低的损耗。93 Ohm一直用于短接续，如连接计算机主机和监视器，其低电容的特点，减少了电路的负载，并允许更长的接续。（注意故事中标红的阻抗值，我们看看是不是真的任性？）

我们不管故事如何曲折跌宕，对于工程师来说，性能是考量一个系统的关键因素。那么50 Ohm到底是不是最好的选择，一个即兼顾损耗，又兼顾功率的平衡数值？

我们用最简单的也是应用最为广泛的同轴电缆做参考。

为了证明这个“平衡”，我们先来复习一下同轴传输线的基础知识。

同轴线是由内导体和外导体组成的双导体微波传输线。结构如下图所示：

同轴线主要工作模式是TEM模，主要用于宽频带馈线，设计宽频元器件；

当同轴线的横向尺寸和波长相比拟时，同轴线中将出现TE和TM模，是同轴线的高次模。

同轴线的场分布图如下：

同轴线的阻抗公式：

同轴线的功率容量：

同轴线的损耗：

根据上文给出的同轴线的相关公式，我们一起举个例子验证一下到底是不是这样子的？

假设同轴线的外导体内径为10mm，内导体外径为d从0.1mm变化到9mm，我们通过Matlab计算看一下他的功率容量和损耗都是怎么个变化曲线。为了简便，我们把公式中的常数设为1。

代码如下：

D=10; %同轴线外导体内径为10mm
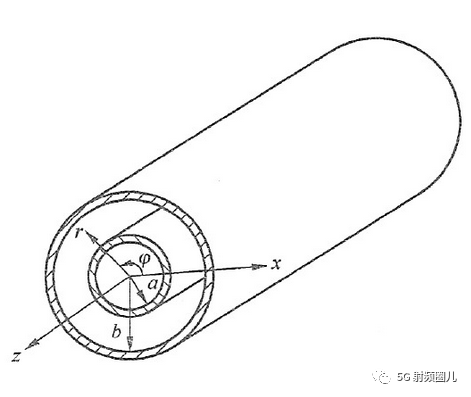
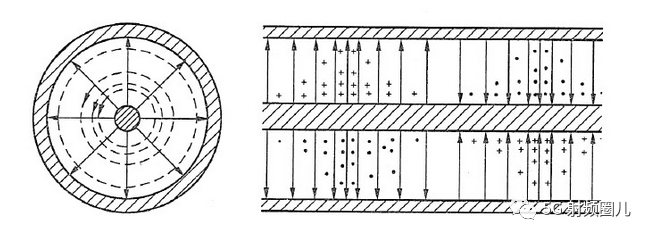
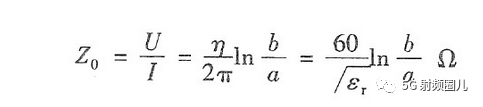
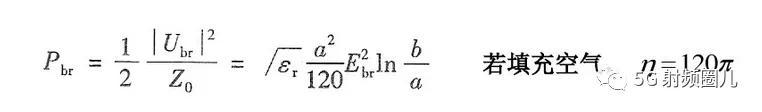
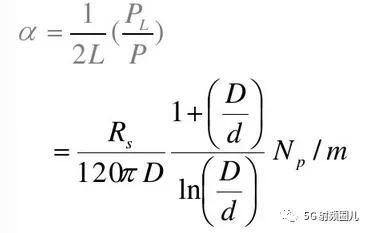
d=0.1:0.1:9; %同轴线内径为变量从0.1mm递增到9mm
%循环计算得到阻抗不同内径的阻抗值和功率容量和损耗值
for i=1:max(size(d))
P(i)=(d(i)*d(i))/120*log(D/d(i));
Z(i)=60*log(D./d(i));
Loss(i)=10/(120*3.14*D)*(1 D./d(i))/log(D./d(i));
end
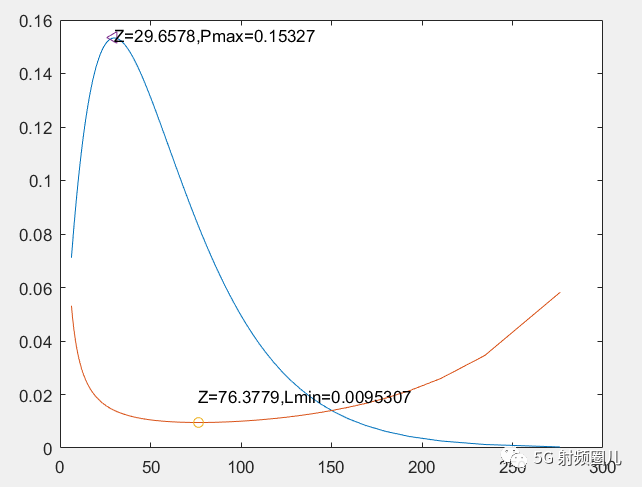
[a,b]=min(Loss); %取得损耗最小值和坐标
[c,d]=max(P);%取得功率容量最大值和坐标
plot(Z,P,Z,Loss)%画图
hold on
plot(Z(b),a,'o');
text(Z(b),a 0.01,['Z=',num2str(Z(b)) ',' ,'Lmin=',num2str(a)]);
hold on
plot(Z(d),c,'<');
text(Z(d),c 0.001,['Z=',num2str(Z(d)) ',' ,'Lmin=',num2str(c)]);
hold off

运行得到：

上图中蓝色线为空气填充同轴线功率容量与阻抗的关系曲线，我们可以看到，当阻抗 Z0=29.6578 Ohm 时，功率容量最大。当阻抗 Z0=76.3779 Ohm 时，同轴线的损耗最小。那么为了得到一个较理想的功率容量，又使得损耗可以接受，我们取这两个特殊阻抗的中间为标准值 Z0=（29.6578 76.3779）/2= 53.0178 Ohm。简便起见，取Z0=50 Ohm. 整个计算结果也印证了前文故事的博弈经过。

到此，我们证明了50 Ohm既不是一个最好的阻抗，也不是一个最差的阻抗，它只是在射频应用中的一个大家都可接受的折中方案。

其实在射频设计中上面两个阻抗极点也是极其重要的。比如在同轴滤波器设计中，我们希望同轴谐振器的损耗最低，那就需要用到 Z=76.3779 Ohm 这个阻抗了。这时候的同轴线内外半径比为：D/d=3.5714时，谐振腔的损耗最低。

当然如果功率容量是设计瓶颈的话，我们也会用到Z=29.6578 Ohm这个特殊阻抗。这个时候同轴线的外径内径比为：D/d=1.6129.

到这里，是不是所有的疑问都解开了？注意我们计算出来的阻抗和故事中的阻抗是不是联系起来了！

阻抗的统一也大大简化了射频设计。试想一下，如果要连接的器件阻抗很任意，是不是很烦人？事实上，我好像被这个东西这么过。当时一个端口要设计成24 Ohm，另一个端口是70 Ohm。测试调试都整的都很难受。

今天就到这里了，希望你有所收获。

射频微波电磁基础

著作权归作者所有，欢迎分享，未经许可，不得转载

首次发布时间：2023-03-08