2 单轴应变寿命疲劳分析(第一部分)
本文摘要(由AI生成):
本文介绍了单轴应变寿命疲劳分析的基本概念和方法。首先,指出了疲劳裂纹的萌生通常源于局部应力集中,而局部应力应变疲劳分析则基于小裂纹萌生前的寿命由局部应力应变序列决定。随后,文章描述了应变-寿命方程,并解释了如何利用该方程从局部应变序列预测疲劳寿命,以及通过应力集中系数计算带缺口部件的疲劳寿命。此外,还讨论了真实应力和应变与工程应力和应变的差异,并指出真实应力应变在分析中的重要性。最后,通过Ramberg-Osgood方程展示了总应变中弹性和塑性分量的关系,强调了真实应力应变曲线在疲劳分析中的应用价值。
2.单轴应变寿命疲劳分析
2.1 简介
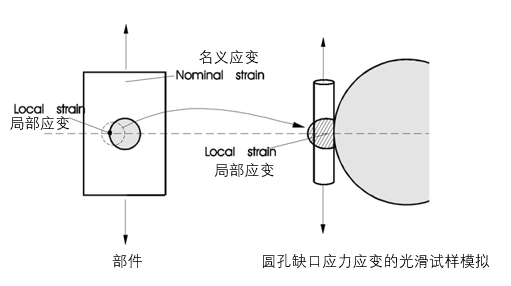
在第一章中展示了:疲劳裂纹通常是由孔和圆角等几何形状引起的应力集中造成的。局部应力应变疲劳分析假定,小裂纹萌生前的寿命由应力集中部位小体积材料中产生的应力和应变序列决定。因此,如果在相同材料的光滑试样上再现相同的应力-应变序列,将获得相同的疲劳寿命。尽管许多工程部件的设计使其在正常工作载荷下的应力和应变低于弹性极限,但在局部应力集中时可能发生屈服,如果疲劳裂纹要萌生,情况必然是如此的。应变寿命分析的应用要求描述材料对循环弹塑性应变的响应,以及这些应变与疲劳寿命之间的关系。本章描述了应变-寿命方程,说明了如何从局部应变序列计算疲劳寿命,并说明了如何使用应力集中系数计算含缺口部件的疲劳寿命。这种疲劳分析方法被称为局部应变寿命、局部应力应变或危险位置分析。局部应变寿命法对于实际的疲劳研究很有吸引力,在疲劳研究中,可以使用应变计测量应变。有限元模型也给出了模型中每个位置的局部应力和应变,因此局部应变寿命法非常适合于使用有限元模型进行疲劳设计。关键位置的应力和应变称为局部应力(σ)和局部应变(ε)。远离缺口且不受其影响的应力和应变为名义应力(S)和名义应变(e)。
2.2 真实应力和应变
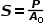 (2.1)真实应力的定义是用荷载除以加载载荷后的实际横截面。
(2.1)真实应力的定义是用荷载除以加载载荷后的实际横截面。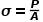 (2.2)
(2.2)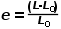 (2.3)
(2.3)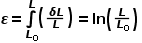 (2.4)真实应变是用应变计测量的应变。由于真实应变是以瞬时应变的增量计算的,因此在分析应变历程时,可以递增地增加或减少,而工程应变则不能。工程应力应变与真实应力应变的差异可以用常规拉伸试验来说明。这通常是根据工程应力和应变绘制的,显示了试样发生颈缩时载荷和应力的降低。图2.3显示了分别作为工程应力应变和真实应力应变绘制的拉伸试验曲线。图2.3 单轴拉伸试验绘制的工程和真实应力应变曲线真实应力一直增加,直至发生破坏。(然而,式2.1至2.4给出的简单关系仅适用于颈缩。缩颈后,应力在截面上的分布不再均匀)。如果 Af 是断裂处的横截面积,σf 是断裂处的真实应力。
(2.4)真实应变是用应变计测量的应变。由于真实应变是以瞬时应变的增量计算的,因此在分析应变历程时,可以递增地增加或减少,而工程应变则不能。工程应力应变与真实应力应变的差异可以用常规拉伸试验来说明。这通常是根据工程应力和应变绘制的,显示了试样发生颈缩时载荷和应力的降低。图2.3显示了分别作为工程应力应变和真实应力应变绘制的拉伸试验曲线。图2.3 单轴拉伸试验绘制的工程和真实应力应变曲线真实应力一直增加,直至发生破坏。(然而,式2.1至2.4给出的简单关系仅适用于颈缩。缩颈后,应力在截面上的分布不再均匀)。如果 Af 是断裂处的横截面积,σf 是断裂处的真实应力。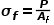 (2.5)
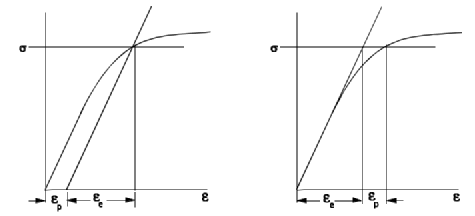
(2.5)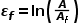 (2.6)单次加载得到的真实应力-真实应变曲线为单调曲线。它由一个弹性部分组成,当负载被移除时,弹性部分被恢复。
(2.6)单次加载得到的真实应力-真实应变曲线为单调曲线。它由一个弹性部分组成,当负载被移除时,弹性部分被恢复。 (2.7)这种关系,由Ramberg(兰伯格)和Osgood(奥斯古德)提出,使用以下定义:图2.4表示了总应变的弹性和塑性分量的两种分析方法。
(2.7)这种关系,由Ramberg(兰伯格)和Osgood(奥斯古德)提出,使用以下定义:图2.4表示了总应变的弹性和塑性分量的两种分析方法。

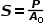 (2.1)
(2.1)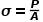 (2.2)
(2.2)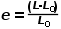 (2.3)
(2.3)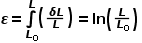 (2.4)
(2.4)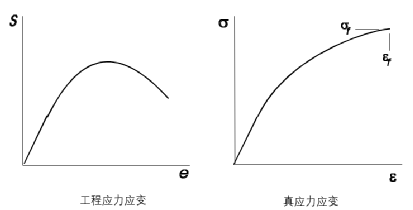
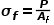 (2.5)
(2.5)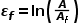 (2.6)
(2.6)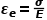

 (2.7)
(2.7)