雷诺眼中的湍流
以下文章来源于LBM与流体力学 ,作者卢比与钢蛋
一百多年前,流体力学界百花齐放:从欧拉和伯努利家族的相遇相知;到纳维遇见斯托克斯成就的白月光;再到布辛涅司克和雷诺共同开启的现代流体力学之门…一个个星光熠熠的名字将流体力学的研究推向了前所未有的高度。他们在研究过程中留下了许多经典,值得我们细细品味。
1884年3月28日,也就是经典的雷诺染色实验的第二年,雷诺受邀来到英国皇家科学院,为学者们带来了一场精彩的报告,题目为 “水流的两种形式”。而同年五月,雷诺的讲座内容即被整理成文章,并刊发于《Nature》。下面为其讲演的主要内容,为了便于理解,笔者添加了一些小标题和配图。
尽管最优秀的数学家付出了巨大的努力,但流体运动的理论仍然无法完全描述实际的流动,而我们并不知道其中的原因。描述流体运动的理论看上去很完整,但是许多情况下,理论的结果和实际却完全不同。如果我们研究雨滴在空中运动的情况,理论能够得到准确的阻力结果。但是如果研究一艘在水中行驶的船,理论计算的阻力结果将和实际常常不一致。而更麻烦的是,我们不知道为什么流体运动的理论适合某些情况却不适合另外一些情况。
七年前,我很荣幸的在这个房间和大家分享过有关旋涡运动的话题。我一直认为,流体运动的理论之所以不够成功,是因为水是均匀清澈的,空气也是透明的,我们看不到任何流体内部的运动。有学者通过对水进行部分着色来显示涡环现象,但是无法全面的展示流动。现在,我大胆的使用了一种全新的方法,我自己称它为“色带法”,这种方法或许能够帮助我们揭示更多流体运动的谜题。
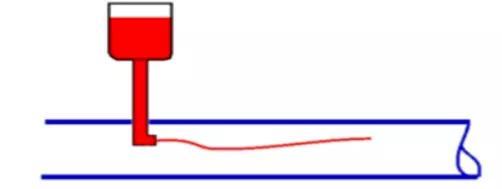
色带法示意图
今晚,我会和大家分享部分验证结果。
首先,为什么流体运动的理论不能像固体一样获得成功呢?答案很简单,通常情况下,固体没有内部运动,固体力学的理论基于内部相对静止的假设,并适用于全部的情况。但是,如果存在某类物体,它有内部运动,通过简单的实验就可以表明实际情况和运动定律的不一致。
如果一个物体被一个绳子悬挂着,大家都知道它会垂直于在悬挂点之下,或者像钟摆一样摆动。但是如果这个物体中间有一个很重的旋转轮,其运动情况则完全不同,它运转起来像个陀螺。
如果这样的物体广泛存在于大自然,那么我们就无法定义规律。例如,苹果具有某种性质,而梨具有另外一种性质,那么运动规律就无法被发现,或者即使发现了梨的运动规律,也无法应用于苹果,这样的理论当然很难令人满意。
而流体就是这种情况。
2. 两种运动方式的类比
今天的主题是水的两种运动方式,并不是说水只有两种运动可能。从一般外观看,水的运动方式是无穷无尽的。
我希望将要展示的现象本身会引起大家的兴趣,不过现象背后的哲学兴趣或许是更加值得深思。流体运动问题可以分为两类,一类是理论结果和实验一致的问题,另一类是完全不同的问题。认识到流体存在两种内部运动形式非常重要,因为我们当前的理论只适用于第一类运动。
我们可以通过类比来解释。大家或多或少都了解军队的运动情况,我们可以将军事战术理论和军队运动之间的关系与水动力学理论和水的运动之间的关系进行类比。
军事战术只能适用于纪律严明的行动,但是外界干扰其秩序时,军队就会采取另一种运动方式。反观水流的状态:在某些情况下,会以一种完全直接,有纪律的方式运动;而在其他情况下,它会变成大量的漩涡和横流,就好像被暴民冲散的军队。

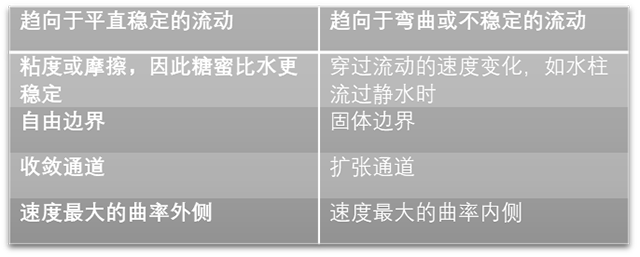
有秩序的运动 VS 混乱的运动
我们还可以进一步的类比:决定军队的运动是规则还是混乱的情况与确定水的运动是笔直还是曲折的情况非常相似。在这两种情况下,秩序都有一定的影响:对军队而言,是纪律;对于水则是粘性。军队的纪律性越好或流体的粘性越强,在任何情况下稳定运动受到干扰的可能性就越小。

纪律严明 VS 纪律涣散
另一方面,更大的运动速度和尺度都会使军队和水流更不稳定。军队越大,行进速度越快,混乱的机会就越大;而对于流体,流动通道越大,速度越快,涡流产生的机会就越大。

小尺度运动 VS 大尺度运动
对于军队而言,不同行进状态的稳定其实也是不同的。在阅兵式上行进的时候几乎是绝对安全的,而在敌人面前则很容易陷入完全混乱的状态,水流也是一样的。即使两个流动的状态都显示是稳定的,但也可能存在根本的差异。对于军队来说,如果一切顺利的话,两种不同难度的演习可能都以稳定的方式进行。但是军队的稳定条件本质上是不同的:对于简单的演习,任何轻微的不协调都很容易得到纠正,而在另一种复杂情况下,它将不可避免地导致混乱。
这种运动方式变化的根源,可以归结为机动性的影响和令人不安的扰乱。在极端微妙的情况下,一个无限小的干扰都可能引起变化。因此,我们可以把军队在简单演习中的状态描述为稳定,而在困难演习中的状态描述为不稳定的,即在最小的扰乱中就会崩溃。小扰乱是崩溃的直接原因,正如声音有时是雪崩的原因一样,但这种崩溃的发生,不稳定的状况才是变化的真正原因。
水的流动类似于上述分析。假设没有扰动,水会以理论中所指出的方式运动。但由于总是有一些轻微的干扰,只有当稳定运动的条件或多或少是稳定的时候,稳定才能存在。
我们需要知道流动在不同情况下是否稳定,而色带法能很好的将两种流动状态区分开,这将有助于改善流体力学理论中一直以来令人不太满意的地方。
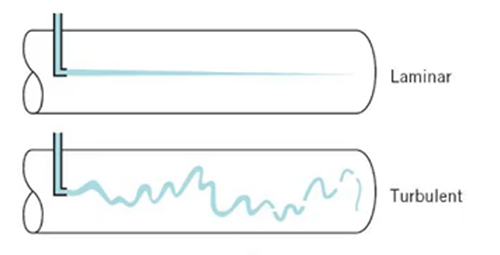
色带法显示的两种流动状态
首先,它表明所有流体的粘性有利于流动稳定,而尺度和速度则具有相反的影响。同时,这些因素的影响服从一个完全确定的规律,即当速度和尺度的乘积除以粘度达到某一特定值时,流动变得不稳定。这条定律解释了迄今为止大量看似矛盾的现象。还有一个普遍的结论,即如果速度足够慢,所有的流动方式都是稳定的。
通过在充满液体的静止烧杯中注入有色颜料,可以很好地显示粘度的影响。当一切完全静止时,将烧杯绕其轴线缓慢转动。烧杯转动时,液体并不会大幅运动,但靠近壁面的有色液体被拖拽形成一个长长的污迹。而只需将烧杯转回去,污迹就会倒流,直到色带恢复原始位置。根据前述的理论,在整个转动过程中,运动是相当稳定的。
当水流稳定时,它就好像一股清澈的水柱。沿着管道流动的水就是这样一条水柱。管道内的水流是以固体壁面为界限的,但是如果水是稳定流动的,我们可以想象水被理想的管道分成一系列无限小的水柱,其中任何一条都可以着色而不改变它的运动,就像一个步兵纵队可以用颜色区别于另一个步兵纵队一样。

层流喷嘴产生的水柱
如果流动存在内部运动的话,我们就不能把被管道包围的整个流动看作是一个稳定的水柱,因为水不断地从管壁的一侧流到另一侧,就像我们无法在剧院的走廊里分辨出人群中的彩色条纹一样。固体壁面对于水柱的形成并不是必须的,喷泉的水流由自由表面包围,而河流则是部分被固体表面环绕。
5. 临界速度的秘密
很长一段时间以来,人们注意到,注入静止流体的流动常处于不稳定状态,也正是这种不稳定性使得火焰和喷流对声音引起的轻微扰动非常敏感。
我现在打开水龙头,以便让一股稳定的有色水流从上面的管子进入,水流从下面的管子流出。彩色的水流笔直地穿过容器,看不到任何其他的运动,它看起来像一根红色的玻璃棒。然而,红色的水流动缓慢,因此粘度的影响最大,而水流是稳定的。随着速度的增加,水流中出现了某种蠕动的、蜿蜒的运动;再快一点,水流就会分裂成美丽而清晰的漩涡,并扩散到周围的水中,这些漩涡随着颜色变得不透明,逐渐给实验蒙上了一层面纱。
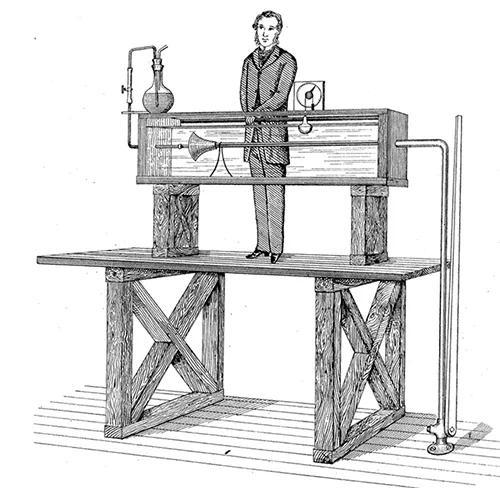
雷诺实验
毫无疑问,水流的最终破裂是由仪器中的一些轻微振动决定的。但这种振动一直存在,直到水流处于一个足够不稳定的状态时,它才对水流产生影响。对于给定尺度和粘度的流动,如果流动速度足够慢,流动就是稳定的。然而在一定的临界速度下,水流将变得不稳定。
当今实验流体力学中还有个引人注目的事实,即水沿着收缩和扩张通道流动的方式不同。水进入的管口是宽的,先收缩一段时间,然后再逐渐膨胀,直到和管口一样宽。进入收缩段以后,流动是稳定的,色带保持其清晰的条纹状特征,直到它到达颈部,在那里收敛停止;然后进入扩张的通道,色带逐渐分裂成漩涡。因此,收缩通道有助于流动稳定,而扩张通道则相反。
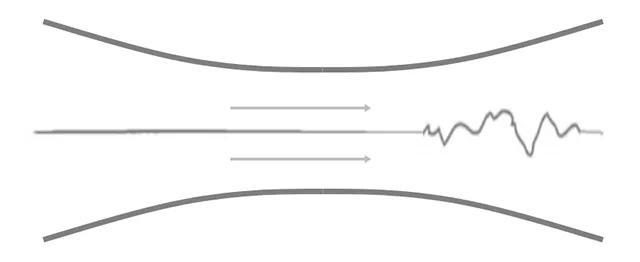
收缩与扩张通道中的流动示意
大家现在看到的现象和船舶在水中行驶并没有什么不同。我们可以假设船是固定的,水流过船身,这和船在水中行驶的效果是一样的。在船的前部,水流是稳定的,因为船体形成了一个收敛的通道。然而,随着水流向船尾,流动扩张形成了不稳定的涡流,这些涡流解释了船舶行驶的阻力和理论计算结果的差异。

船体周围的流动
如果我们有一个平行通道,既不收缩也不扩张,那么稳定的流动将是一堆稳定的平行流,它们都在流动,但速度不同,中间部分的流动速度最快。
众所周知,水流会遇到阻力。在河流和所有适中尺寸的管道中,一般经验表明阻力随着速度的平方而增加,而在非常小的管道中,如动物的静脉,泊肃叶证明阻力随着速度而增加。因此,对于不稳定的紊乱流动来说,阻力和速度的平方相关,而平直的温和流动中,阻力和速度相关。
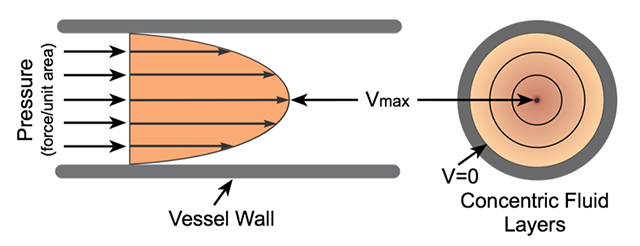
静脉血管中稳定流动的速度分布
那么如果能够证明根据管道尺寸,在足够大的速度下,运动变得不稳定,则可以解释这种差异。而我们的色带实验恰好证明了这一点,当流速很低的时候,流动是非常稳定的,随着速度的增加,色带自然变得更细,但当达到一定速度时,色带变得不稳定,并与周围充满管道的流体混合。这种蜿蜒的运动是在一定的速度时发生的,如果把速度减得很小,色带又会变得笔直而清晰,再增加一次,色带又会破裂。这个临界速度取决于管子的大小,以精确的反比表示,管子越小,则需要的速度越大。而流体的粘性越大,需要速度也就越大。
至此,我们完整的解释了一般情况下的阻力结果和泊肃叶所发现的阻力定律之间的差异。
8. 油阻波的一种解释
我们还可以提供完整的证据来证明固体表面之间的稳定流仍然存在一定的不稳定性,然而这种不稳定性的原因尚未完全确定。可以肯定的是,尽管壁面的侧向刚度并不重要,但平行于流动的切向刚度对于涡流的产生至关重要。
我无法向各位展示这一点,因为我们能够创造的唯一方法是在水面上吹风。当风吹过水面时,它会像移动的固体壁面一样向水表面传递运动。以这种方式运动的水体内部不易受涡流影响,但它的表面并不稳定,会生成波浪。
一个非常古老的实验证明了这一点,最近也引起了大家的注意:如果把油放在水面上,它会散布成仅具有固体表面特征之一的无限薄的薄片,它提供的阻力很小,但仍能抵抗伸缩,并足以完全改变流动的性质。风的作用使水面以下产生旋涡,它使水体内部不稳定,但不在表面产生波浪。

人们曾向海面泼洒油脂以削弱海浪
对于那些观察到油阻波现象的人来说,在整个力学领域可能没有什么比这更让人震撼的了。一层如此薄的油膜,我们无法说明其厚度,并且除了它的效果外,其他无法感知。它不具有我们所能察觉到的机械性能,但却能够阻止一种我们所能想象到的最强大的力量——这种力量能够使我们的船只翻倒并破坏海岸。
然而,当我们意识到油并不是纯粹靠力量使海洋平静下来,而仅仅是通过改变了风的作用所产生的流动方式,使之从海面可怕的波浪转变为海面以下无害的漩涡时,这一点就变得可以理解了。
如果我们考虑水以外的其他流体,比如油或糖浆,显然比水流动得更慢更稳定。然而,这只是在较小的流动尺度中。如果大自然产生了泰晤士河大小的糖浆河,糖浆就会像水一样容易流淌。因此,在火山喷发的熔岩流中,尽管熔岩有着布丁般的稠度,但在山下巨大而快速的流动中,熔岩像水一样随着漩涡流动。

熔岩的湍流形态
尽管在一百多年前,人们还不知道层流、湍流和转捩这些概念,雷诺数也未正式命名。可是,雷诺却通过简单的设备向我们完整的展示了流态的变化,并阐述了流体力学理论和实际流体运动之间的关系,即便在今天读来,仍然带给我们很多思考。
著名的空气动力学家库奇曼曾说过:“每一种具体的理论都是暂时的,而对流动本质的理解却是永恒的”。




