统计分布讲解

3年前浏览2231

过冷水诚挚邀请你加入Matlab仿真秀官方交流群进行Matlab学习、问题咨询、 Matlab相关资料下载，群号：927550334

概率论是一门数学学科，它与几何或分析力学等学科有很相似的目标。之前有一直和大家讲Monte Carlo、分布函数、抽样方法，高端的玩家往往会用最基本的东西玩出不一般的花样，本期过冷水和大家一起学习Matlab有关数据统计和随机变量分布的入门知识。

随机现象中，变量的取值是不确定的，称之为随机变量。描述随机变量取值概率的函数称为概率分布。对于随机变量，通常主要关心它的两个主要数字特征：数学期望用于描述随机变量的平均值，方差用于描述随机变量分布的差异程度，方差的算术平方根称为均方差。另外协方差和相关系数用于描述两个变量的线性关联程度。

随机变量的分布根据其取值特点不同主要分为离散型和连续型两类，若用ζ表示实验投硬币计正方面次数，“正面向上次数”，其取值可能为0,1,2,.....10,则为离散型随机变量。典型的离散型分布有离散均匀分布、二项分布、Possion分布等。若用变量η表示学生群体的身高分布，其取值可能在[1.5,2.5]中任何值，则为连续型随机变量。典型的连续型分布有均匀分布、正态分布、指数分布、χ²分布、t分布、F分布。

统计分布函数：

y = pdf('name',x,A,B,C,D)

Name:表示具体分布类型；x：随机变量；A、B、C、D:不同分布对应的参数。

常见概率分布密度函数如下表：

中文函数名	调用名称	输入参数A	输入参数B	输入参数C	输入参数D
Beta分布	Beta	a第一个形状参数	b第二个形状参数	——	——
二项分布	Binomial	n实验次数	p 每次成功实验的概率	——	——
卡法分布	Chisquare	v自由度	——	——	——
指数分布	Exponetial	u均值	——	——	——
F分布	F	v1分子自由度	v2分母自由度	——	——
Gamma分布	Gamma	a形状参数	b尺度参数	——	——
几何分布	Geometric	ρ概率参数	——	——	——
超几何分布	Hypergeometric	m总体的大小	k总体所需特征项数	n抽取样本数	——
对数分布	Lognormal	u对数值均值	σ对数值的标准差	——	——
负二项分布	Negative Binomial	r成功次数	p单个实验成功概率	——	——
非中心F分布	Noncentral F	v1分子自由度	v2分母自由度	δ非中心参数	——
非中心t分布	Noncentral t	v自由度	δ非中心参数	——	——
非中心卡方	Noncentral Chi-square	v自由度	δ非中心参数	——	——
正态分布	Normal	u均值	σ标准差	——	——
泊松分布	Poisson	λ均值	——	——	——
瑞利分布	Rayleigh	b尺度参数	——	——	——
T分布	T	v自由度	——	——	——
均匀分布	Uniform	a下部端点	b上部端点	——	——
离散均匀分布	Discrete Uniform	n最大可观测值	——	——	——
Weibull分布	Weibull	a尺度参数	b形状参数	——	——

离散均匀分布案例：

设一个随机变量ζ服从离散均匀分布，如果其概率为

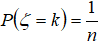
则其分布函数为：

代码：

n=20;x=1:n;

y = pdf('Discrete Uniform',x,n);

%绘制分布图像

figure1 = figure;

axes1 = axes('Parent',figure1);

hold(axes1,'on');

plot(x,y,'MarkerFaceColor',[0 0.447058826684952 0.74117648601532],'MarkerEdgeColor',[0 0 1],'Marker','o','LineWidth',2,'Color',[1 0 0]);

ylabel('概率分布');xlabel('随机变量');

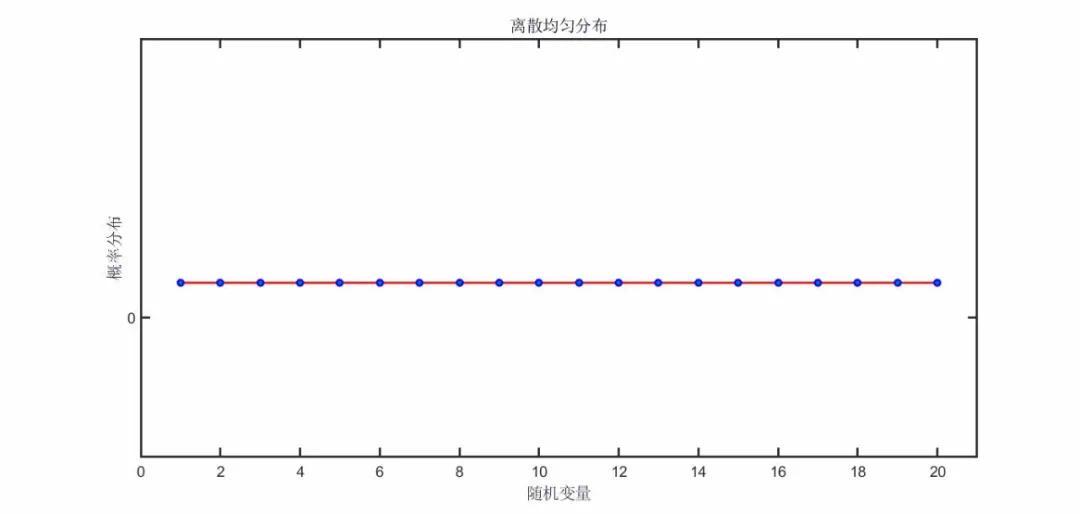
title('离散均匀分布');

xlim(axes1,[0 21]);ylim(axes1,[-0.2 0.4]);

box(axes1,'on');

hold(axes1,'off');

set(axes1,'FontSize',14,'LineWidth',2,'YTick',[-0.2 -0.14 -0.08 -0.02 0.04 0.1 0.16 0.22 0.28 0.34 0.4 0.4]);

%储存图像

% pwd是获取当前运行目录

filename=[pwd,'\','离散均匀分布'];

print(filename,figure1,'-r600','-dtiffn');

若将实验可能结果分为两个：A发生、A不发生，则称此随机实验为二项分布：

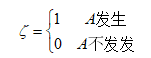
那么ζ服从一个简单离散分布P(ζ=1)=p,P(ζ=0)=1-p,称为二项分布。将二项分布实验独立重复进行n次，称为n重二项分布，n重二项分布实验中A发生的次数分布为：

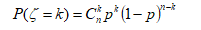
称为参数为n、p的二项分布：ζ~B(n,p)。

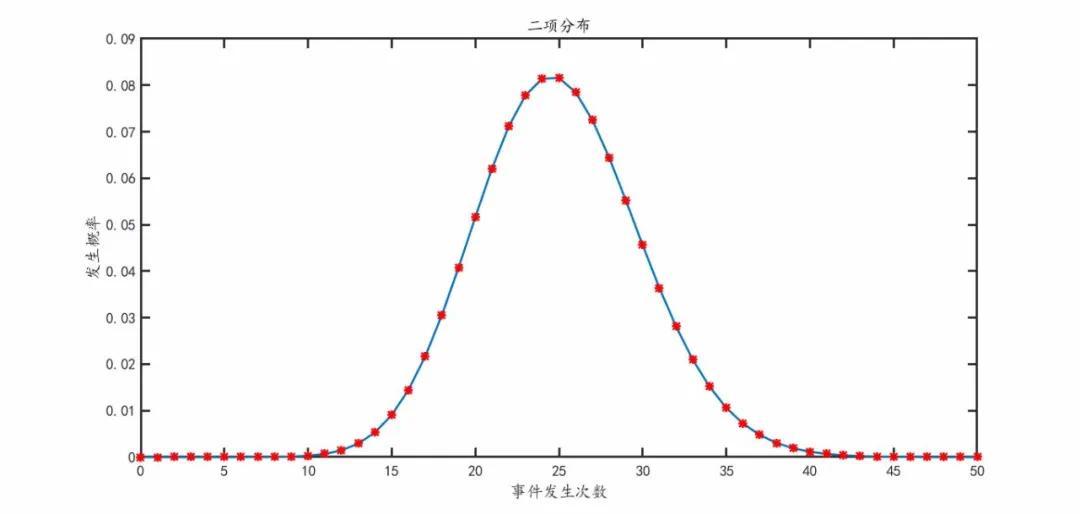
代码：

x=0:50;

n=500;P=0.05

y = pdf('Binomial',x,n,p);

%绘制分布图像

figure1 = figure;

axes1 = axes('Parent',figure1);

hold(axes1,'on');

plot(x,y,'MarkerFaceColor',[1 0 0],'MarkerEdgeColor',[1 0 0],'MarkerSize',8,'Marker','*','LineWidth',2);

ylabel('发生概率');xlabel('事件发生次数');

title('二项分布');

box(axes1,'on');

hold(axes1,'off');

set(axes1,'Clipping','off','FontName','楷体','FontSize',14,'LineWidth',2);

%储存图像

% pwd是获取当前运行目录

filename=[pwd,'\','二项分布'];

print(filename,figure1,'-r600','-dtiffn');

均匀分布

连续型概率分布的表达式与离散型有很大不同，因为连续型随机变量取值是无法列举的，况且在单个点取值的概率总是0。连续型概率分布是用密度函数来表示。相应随机变量取值的概率可通过对密度函数积分得到。

均匀分布密度函数：

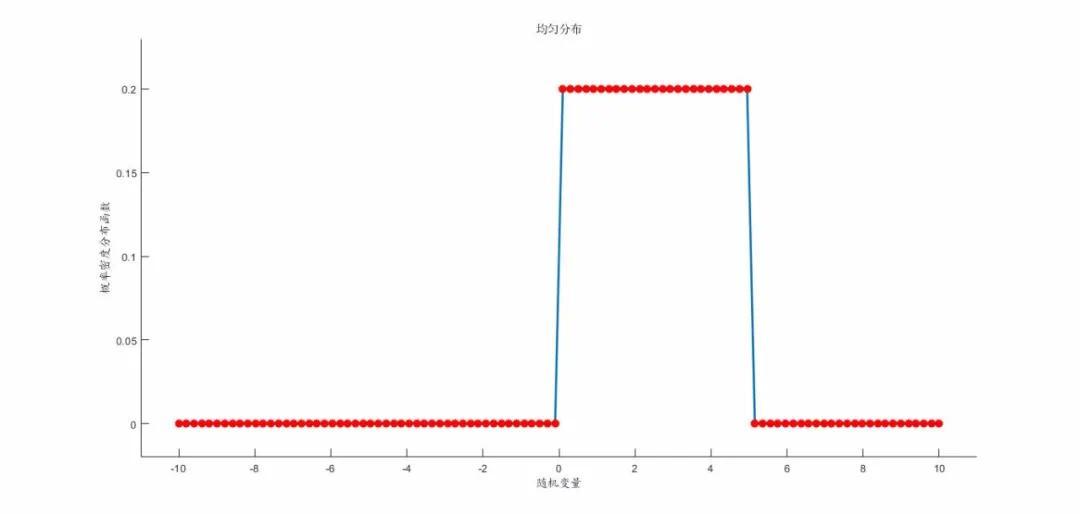
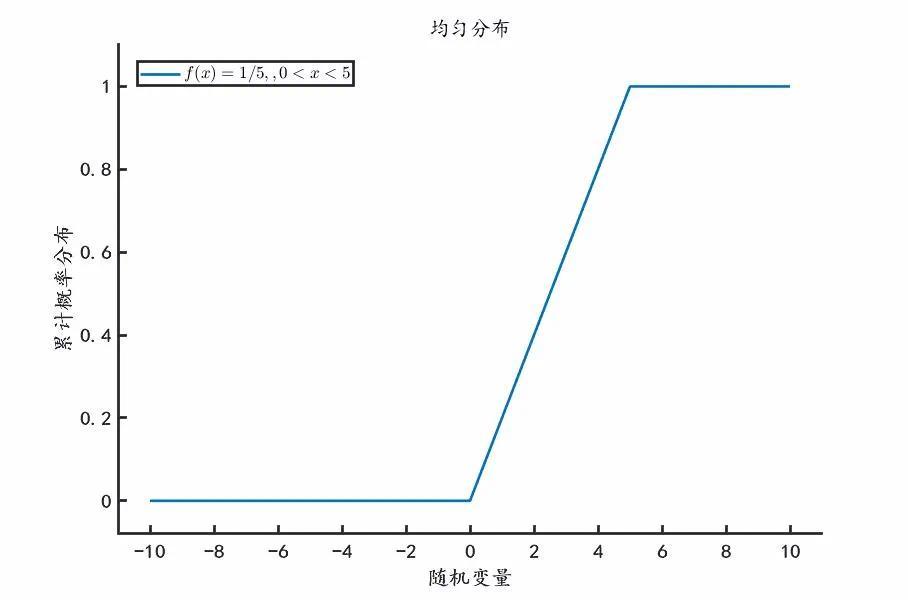
代码：

x=linspace(-10,10,100)

p=1/5;

pd = makedist('Uniform',p);

y = pdf(pd,x);

%均匀分布的累计概率分布

syms x

x1=linspace(-10,0,100);

x2=linspace(0,5,100);

x3=linspace(5,10,100);

y1=linspace(0,0,100);

f=@(t)(1/5);%概率密度分布；

y2=double(arrayfun(@(t)(int(f,x,0,t)),x2));

y3=linspace(1,1,100)

%绘制分布图像

int(1/5,x,0,5)

figure1 = figure;

axes1 = axes('Parent',figure1);

hold(axes1,'on');

plot(x,y,'MarkerFaceColor',[1 0 0],'MarkerEdgeColor',[1 0 0],'Marker','o','LineWidth',2);

ylabel('概率密度分布函数','FontName','楷体');

xlabel('随机变量','FontName','楷体');

title('均匀分布');

xlim(axes1,[-11 11]);

ylim(axes1,[-0.02 0.23]);

hold(axes1,'off');

% 设置其余坐标区属性

set(axes1,'FontName','楷体','FontSize',14,'FontWeight','bold','LineWidth',2,'YMinorTick','on','YTick',[-0.02 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 0.2 0.22 0.23]);

%绘制累计概率分布

figure2 = figure;

axes1 = axes('Parent',figure2);

hold(axes1,'on');

plot([x1 x2 x3],[y1 y2 y3],'DisplayName','$f(x)=1/5, ,0<x<5$','LineWidth',2);

ylabel('累计概率分布','FontWeight','bold','FontName','楷体');

xlabel('随机变量','FontWeight','bold','FontName','楷体');

title('均匀分布');

xlim(axes1,[-11 11]);

ylim(axes1,[-0.08 1.1]);

hold(axes1,'off');

set(axes1,'FontName','楷体','FontSize',14,'FontWeight','bold','LineWidth',2);

legend1 = legend(axes1,'show');

set(legend1,'Position',[0.150457307741795 0.856255571979886 0.239467178461172 0.0402666677951811],'Interpreter','latex')

%储存图像

% pwd是获取当前运行目录

filename1=[pwd,'\','均匀分布'];

filename2=[pwd,'\','累计概率分布'];

print(filename1,figure1,'-r600','-dtiffn');

print(filename2,figure2,'-r600','-dtiffn');

正态分布

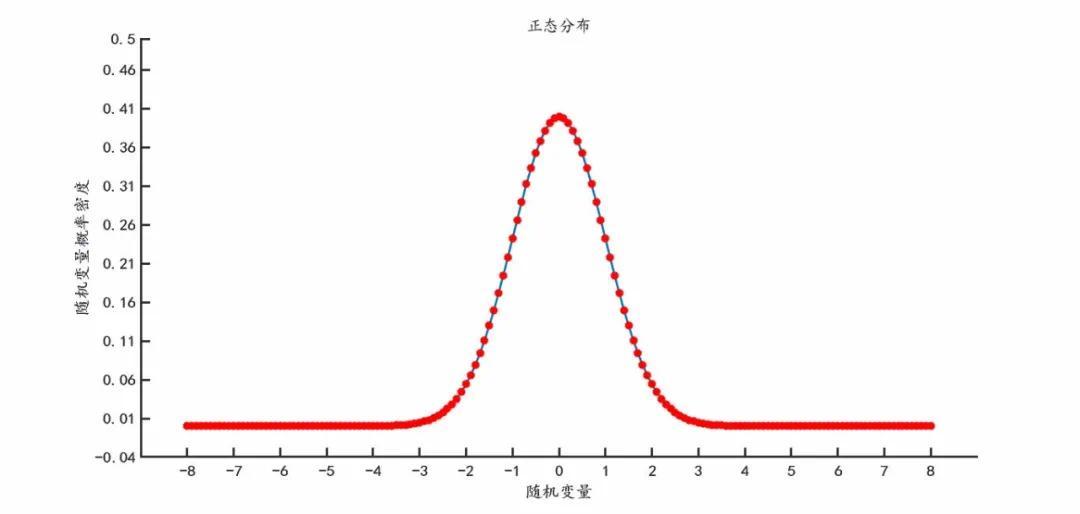
正态分布是应用最广泛的一类概率分布，其概率密度为：

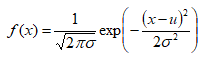
记为N(u,σ²)，其中u是随机变量取值的平均，而σ表征了随机变量取值的差异。特别地，N(0,1)称为标准正态分布。

代码：

x=-8:0.1:8;

mu=0;sigma=1;

pd = makedist('Normal',mu,sigma);

y = pdf(pd,x);

%正态分布的累计概率分布

syms x

x1=-8:0.1:8;

mu=0;sigma=1;

f=@(x)((1./sqrt(2*pi*sigma)).*(exp((-(x-mu).^2)./(2*sigma.^2))));%定义原始积分项函数；

y1=arrayfun(@(x)(quad(f,-8,x)),x1);

%绘制分布图像

figure1 = figure;

axes1 = axes('Parent',figure1);

hold(axes1,'on');

plot(x,y,'MarkerFaceColor',[1 0 0],'MarkerEdgeColor',[1 0 0],'Marker','o','LineWidth',2);

ylabel('随机变量概率密度');

xlabel('随机变量');

title('正态分布');

xlim(axes1,[-9 9]);

ylim(axes1,[-0.04 0.5]);

hold(axes1,'off');

set(axes1,'FontName','楷体','FontSize',14,'FontWeight','bold','LineWidth',2,'XTick',[-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8],'YTick',[-0.04 0.01 0.06 0.11 0.16 0.21 0.26 0.31 0.36 0.41 0.46 0.5]);

%累计概率分布图像

figure2 = figure;

axes1 = axes('Parent',figure2);

hold(axes1,'on');

plot(x1,y1,'DisplayName','$F(X)=\int_{-8}^{t}f(t)dt$','LineWidth',2);

text('Parent',axes1,'FontWeight','bold','FontSize',14,'Interpreter','latex','String','$N(\mu={0},\sigma^{2} ={1})$','Position',[-7.26031294452347 1.03435582822086 0]);

ylabel('累计概率');

xlabel('随机变量');

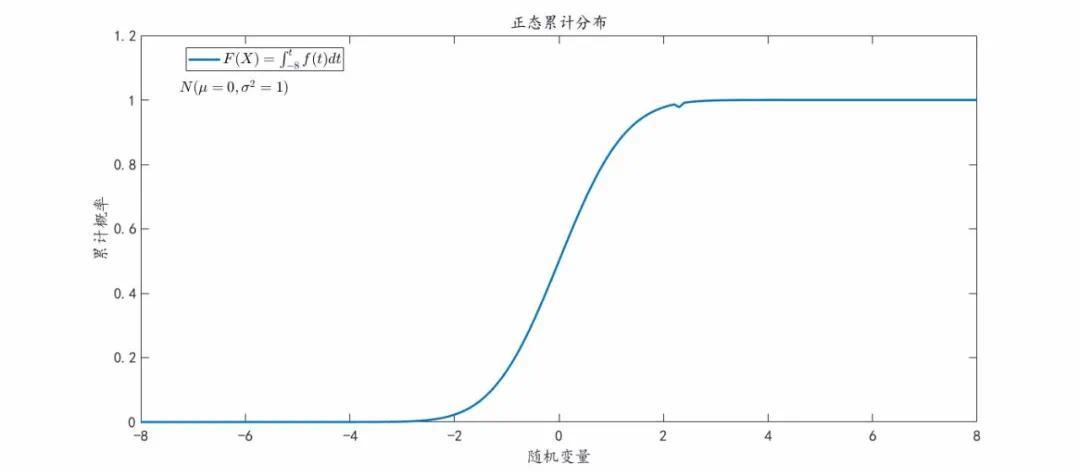
title('正态累计分布');

box(axes1,'on');

hold(axes1,'off');

set(axes1,'FontName','楷体','FontSize',14);

legend1 = legend(axes1,'show');

set(legend1,'Position',[0.134682450787465 0.850159728422969 0.220896033581171 0.049125053411969],'Interpreter','latex','FontSize',14);

%储存图像

% pwd是获取当前运行目录

filename1=[pwd,'\','正态分布'];

filename2=[pwd,'\','正态累计分布'];