Matlab与傅里叶变换

3年前浏览1679

过冷水最近这个段时间给大家讲了好几期傅里叶级数展开，本期作为收尾工作，将会清楚明白的告诉大家傅里叶变换是怎么回事。

傅里叶级数实际实际是对周期函数和半周期函数的按基地函数去1、cosx、cos2x、...cosnx、sinx、sin2x、sinnx的展开式。如果定义在（-∞，∞）区间的非周期函数还能进行傅里叶展开吗？傅里叶计算扩展到连续变换的情况后就是傅里叶积分。

已知周期为2π的函数用傅里叶展开式形式如下：

则周期为2L的函数用傅里叶展开为：

对微分变换过程有疑问的可以查看过冷水往期推文积分变量替换到legendre微分变换。如果L→∞，则该函数就不在具有周期性，而且区间变成（-∞，∞）。我们一起来看傅里叶级数展开式会发生哪些变化：

则：

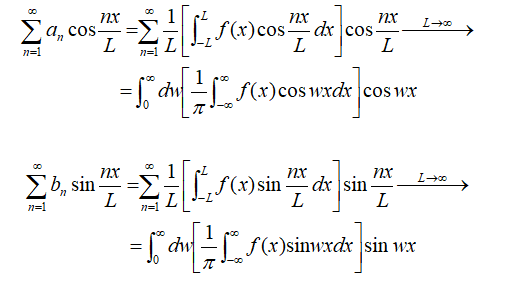
则f(x)变为：

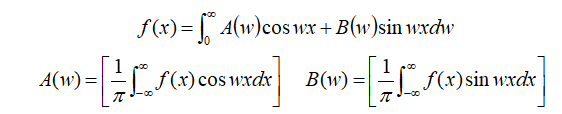
该函数表达式就是函数f(x)的傅里叶积分表达式。物理上通常认为f(x)代表一个“信号”系数A(w)和B(w)是信号f(x)的频谱分布函数，由信号得到频谱的过程叫做傅里叶分析。

给个实例来演示一下傅里叶积分变换：

Matlab计算代码:

syms w
X=linspace(-10,10,300);
for i=1:length(X);
    x=X(i);
    f=(2.*cos(w.*pi/2)*cos(w.*x))./(pi.*(1-w.^2));
    F(i)=vpa(int(f,w,0,100));
end
figure1 = figure;
axes1 = axes('Parent',figure1);
hold(axes1,'on');
plot(X,F,'LineWidth',2);
xlabel('$x$','Interpreter','latex');
ylabel('$f(x)$','Interpreter','latex');
box(axes1,'on');
ylim(axes1,[-0.02 1.2]);
set(axes1,'FontSize',16,'LineWidth',2);

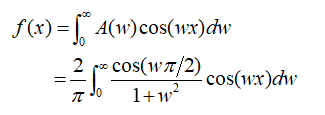
Matlab计算代码:

syms w
X=linspace(-10,10,100);
for i=1:length(X);
    x=X(i);
    f=(2.*cos(w.*pi/2)*cos(w.*x))./(pi.*(1-w.^2));
    F(i)=vpa(int(f,w,0,100));
end
figure1 = figure;
axes1 = axes('Parent',figure1);
hold(axes1,'on');
plot(X,F,'LineWidth',2);
xlabel('$x$','Interpreter','latex');
ylabel('$f(x)$','Interpreter','latex');
box(axes1,'on');
ylim(axes1,[-0.02 1.2]);
set(axes1,'FontSize',16,'LineWidth',2);

傅里叶积分是很接近傅里叶变换的形式，将频谱w∈[0,∞]变成w∈[-∞,∞]，我们来看一下怎样将一个函数进行傅里叶变换。

函数的傅里叶积分形式：