PFC颗粒分析第一步:掌握离散元这些成样方法就够了!
- 作者优秀
- 优秀教师/意见领袖/博士学历/特邀专家/独家讲师
- 平台推荐
- 主编推荐/内容稀缺

导读:PFC是一个关于颗粒的方法,在进行分析的时候我们首先需要做的就是生成一个比较好的式样,这篇文章从简单的create开始,介绍规则与随机颗粒的生成,从create角度去理解generate与distribute的建模思路。之后再介绍基于generate方法的压缩法、分层压缩法、分层欠压法(UCM)、粒径膨胀法,还有基于distribute的网格法(GM),还会介绍PFC自带的Brick方法。有集成的命令流,也有自开发的fish,有一些fish还是比较难理解的,对于各位的fish基础可能会是一个比较大的挑战。
我个人还是建议各位可以将这文章打印下来好好理解,对于理解离散元和加强fish学习都是一个比较好的机会。
一、最原始的成样——Create
Create应该是PFC最底层的成样关键词了,后面所有的成样关键词都是在这个关键词基础上建立了。Create的使用也很简单,只需要指定位置(position)和半径(radius)就可以了。如图1便是在我们的软件中生成一个圆心在原点,半径0.006的颗粒。

图1.1:create生成的单个颗粒代码及结果
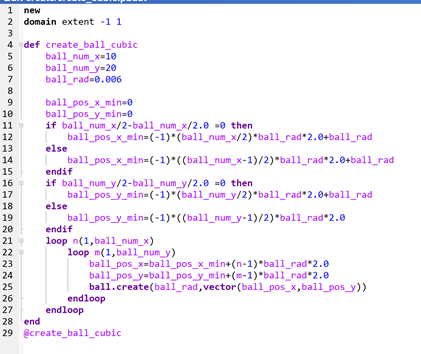
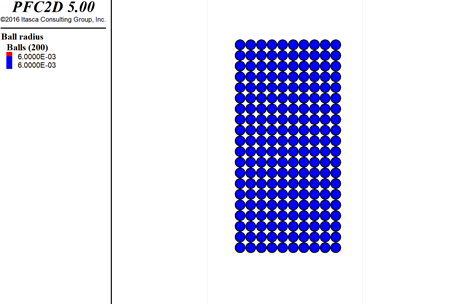
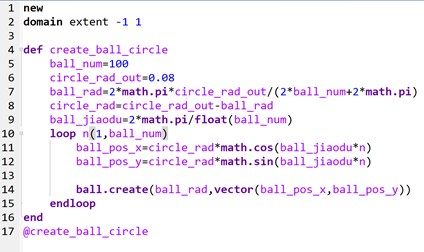
最底层的功能有了,在这个功能上我们便可以去构建一些我们需要的功能,对于做结构物的同学来说,往往需要规则排列的颗粒去模拟结构物。最常见的桩梁结构往往是矩形规则排列的颗粒,我们便可以利用fish语言去构建矩形排列和圆形排列的颗粒,如图2所示。这里面我们使用了ball.create函数,这个函数需要至少两个参数,第一个是一个浮点型变量,表示颗粒的半径,第二个是一个vector变量,表示颗粒的位置。
对于岩土专业,我们需要的应该是随机排列的颗粒,这里也可以使用create实现,我们采用随机数的概念,加上一些边界条件便可以实现这个功能。随机数的概念就不去讲了,这里需要理解一下随机分布的边界条件:颗粒之间没有重叠,大重叠会引起很大的速度,所以我们是不会允许颗粒之间有重叠量。这里代码中有两个函数,第一个函数用于判定一个位置vector和已经生成的颗粒有没有重叠量,第二个函数用于在0.2*0.4范围内生成指定数目指定粒径的颗粒。
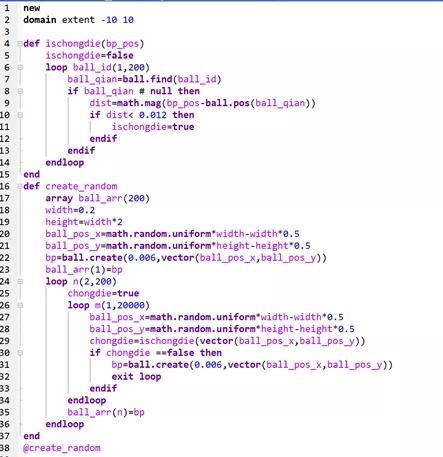

图1.4:create生成的随机排列颗粒代码及结果
到这里很多同学就已经发现了,这不是generate方法吗?没错,是的!genrate的底层就是在create基础上进行的包装。下面我们对generate方法进行讲述。
二、无重叠的成样方法—generate
generate方法是在指定区域内生成无重叠的指定粒径的颗粒,一个最简单的应用就是对前述create的包装。


图2.1:generate生成的随机排列颗粒代码及结果
对矩形规则排列的颗粒也有比较好的实现,需要注意的是指定cubic后,number就没用了,颗粒会铺满区域。这个区域指的是圆心在区域内,而不是颗粒整个在区域内,这里建立一个wall box来可视化一下这个边界,从图中可以看出我讲述的意思。
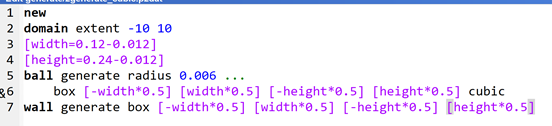
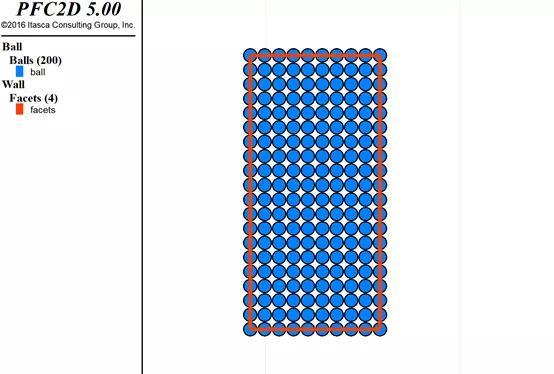
2.2:generate生成的矩形规则排列颗粒代码及结果
在岩土材料中,我们一般要指定颗粒的孔隙率和级配,用generate怎么实现呢?因为generate只能生成指定数量,所以我们需要算出级配中每个粒径颗粒对应的数目。逻辑为:试样颗粒体积 Vs=(1-poro)*V ,其中poro为孔隙率,V为试样体积。如果两个颗粒的质量百分比一样的话(如果密度一样,体积百分比也一样),两个粒径的颗粒体积为 Vs1=Vs2=Vs*0.5 。一个颗粒的体积为 pi*r*r ,这样颗粒数为 Vs1/(pi*r*r)。于是乎命令流为:

图2.3:generate生成的指定孔隙率颗粒的代码
运行上述代码时我们发现了报了一个警告:
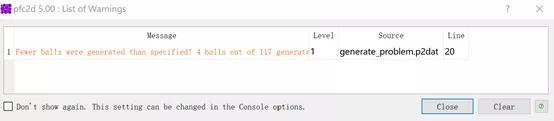
这个警告告诉我们颗粒数目没有达到指定的数目,我们看一下模型图:
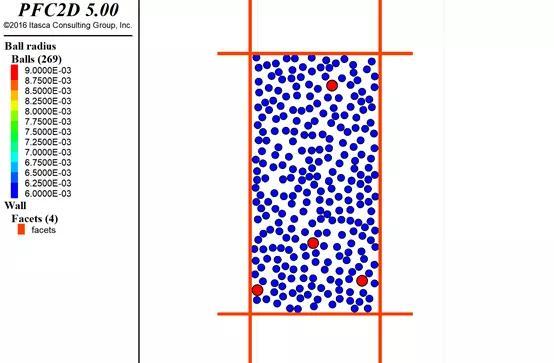
图2.5:模型图
通过模型我们可以发现,0.006粒径的颗粒基本上可以了,但是0.009粒径的颗粒却只有4个,远远没有满足要求。这里原因可以去理解一下我create生成随机分布的代码,里面设定了一个数字是20000,这个数字代表着在找不重叠的位置的时候,只会寻找20000次,超过这个次数便放弃生成这个颗粒。generate里面也是一样的,默认搜索次数是20000,对应的关键词是tries。
所以暴露出了generate方法的一个缺点了,就是很难在生成指定孔隙率的颗粒,原因是在指定空间中,不足以生成指定数目指定粒径的颗粒。那有没有解决的办法呢?当然是有的,对应上述三个边界条件——“指定空间"、”指定粒径“、”指定数目“,产生三种方法。我们一个个来讲。
三、“指定空间”的解决办法——压缩法
压缩法的概念是,保持粒径不变,我先将区域放大,然后移动墙体,使其移动到指定的区域面积。以下为这个逻辑的demo,区域放大系数为5.0,也就是先将区域放大五倍,然后移动上部墙体,移动4.0倍的区域距离。下为压缩法的代码:
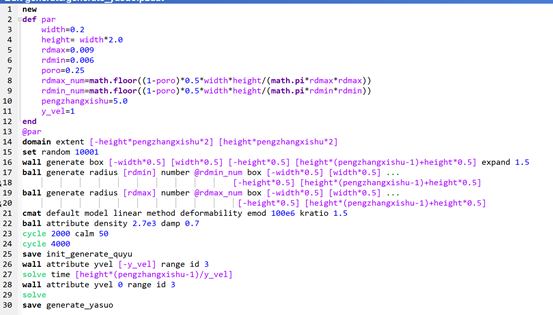
图3.1:压缩法代码
首先我们在一个比较大的范围内生成颗粒:
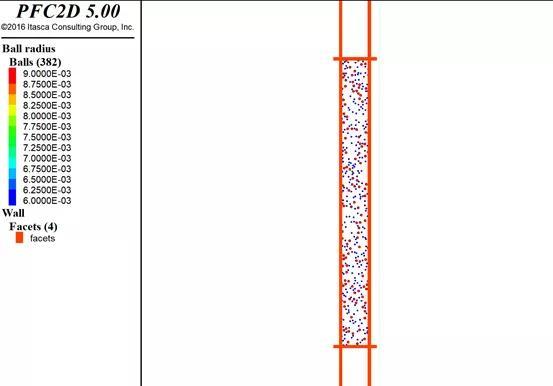
图3.2:压缩前模型
之后压缩到指定的尺寸:
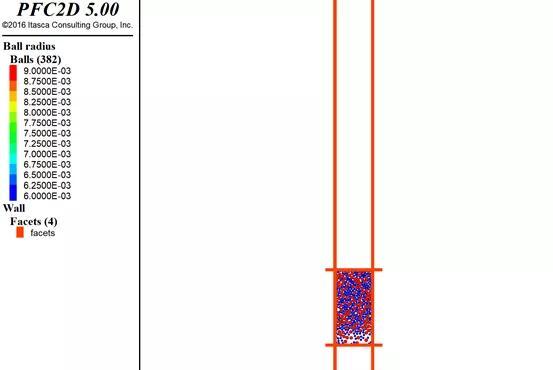
图3.2:压缩后模型
可以看出来,虽然生成了指定数目的颗粒了,但是试样在上方比较密,在下方比较松,这样必然会导致试样的不均匀性,于是很多学者对其进行了拓展,基本的拓展方法为分层压缩法。分层压缩法将压缩分成好几层,这样由于压缩底部的空隙被分担到每层中,式样的均匀性就有了很大的提高。

图3.3:分层压缩法代码
这里分5次成样,下面给出执行中的试样状态:
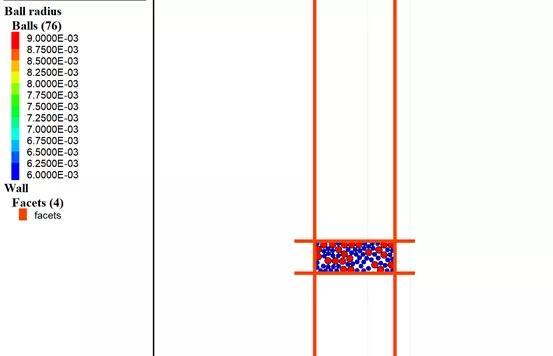
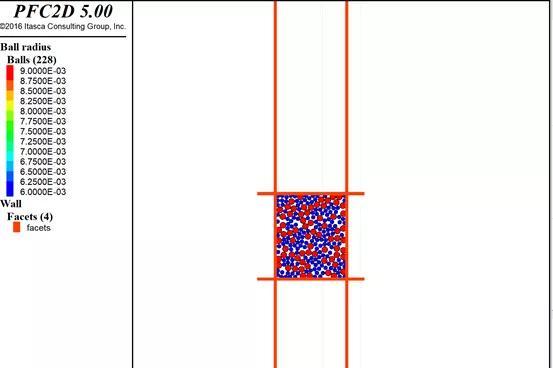
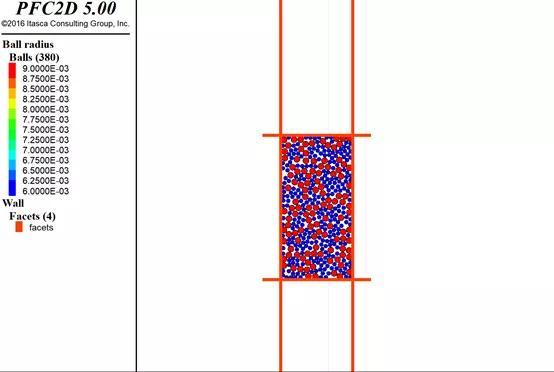
很多学者对于压缩时候的能量传递进行研究,认为由于压缩能的影响,下部的颗粒在成样的时候应该松一点,上部的颗粒应该密一点。这时候我们可以改变孔隙率实现这个想法,具体为:如分5层,则5层的孔隙率为 1.08*poro,1.04*poro,poro,0.96*poro,0.92*poro。这个可以根据试样的情况去调。也有一些学者对孔隙率的值进行了定值研究,国内比较著名的就是分层欠压法UCM(蒋)。
所谓的UCM法基本的概念为其认为压缩的时候墙体对于颗粒有压缩能,压缩能的存在导致了分层压缩的时候,上部颗粒会相对较松,而下部较密。这个概念当然是早就有了,UCM的创新之处在于其提出了孔隙率随着层数的分布,有一个初始欠压比的概念,通过调整初始欠压比,便可以实现对所有层孔隙率的调整。下面给出分层欠压法的代码:
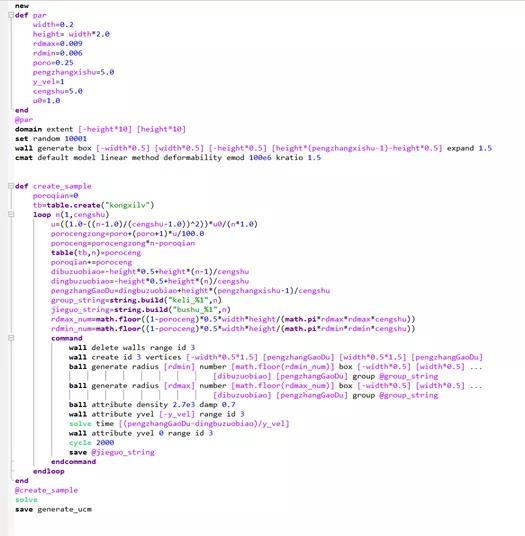
这里的u0决定了孔隙率的分布,u0等于1.0时,孔隙率的分布为(注意我们目标孔隙率为0.25):
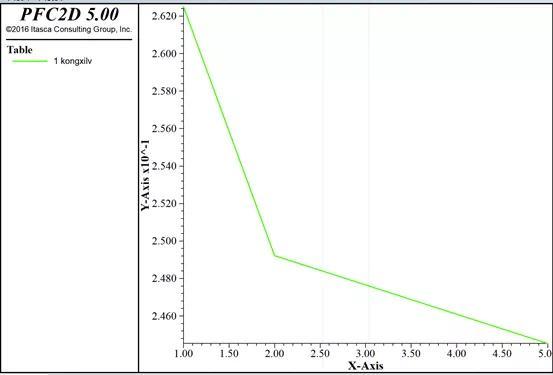
图3.6:分层欠压法孔隙率分布
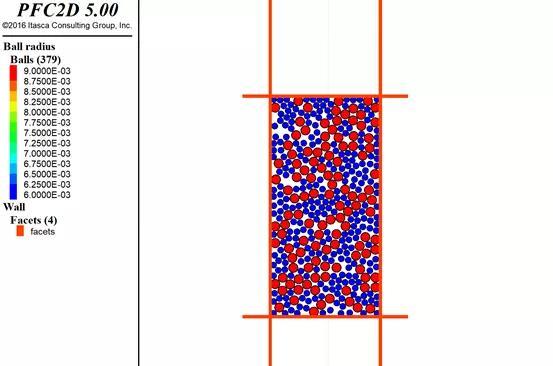
图3.7:分层欠压法结果
四、“指定粒径“的解决办法——粒径膨胀法
这个思路就是先将粒径减小,生成指定数目后,再将粒径增大。这里给出demo,这里定义了膨胀系数为5.0,就是先将粒径减小五倍,之后再放大。
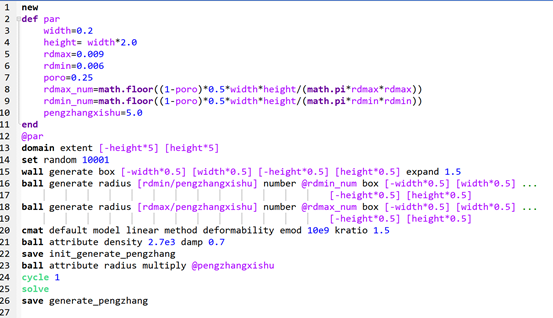
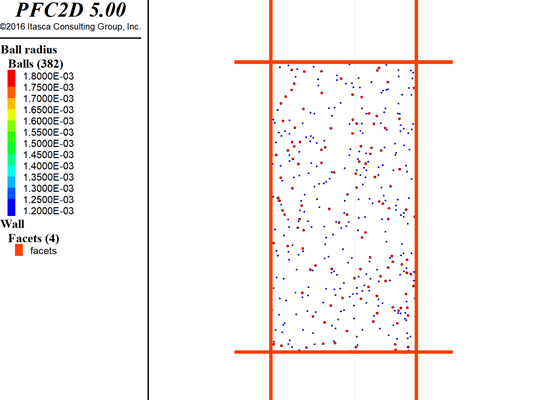
图4.2:粒径膨胀法粒径放大前
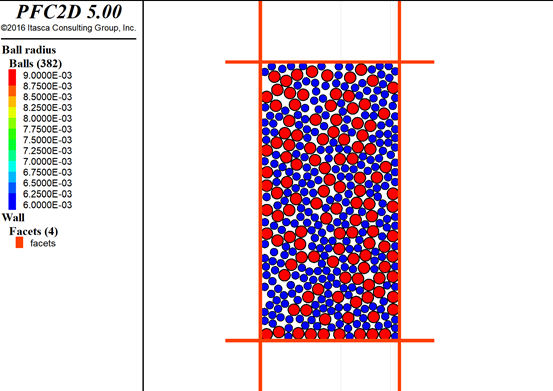
图4.3:粒径膨胀法粒径放大后
这个方法的概念比较简单,就不多赘述了。
五、“指定数目“的解决办法——“强行塞”
这个思路什么意思呢,就是我这里不管你的重叠量了,我直接往区域内塞入指定数目的颗粒,力学平衡后形成我们的式样。
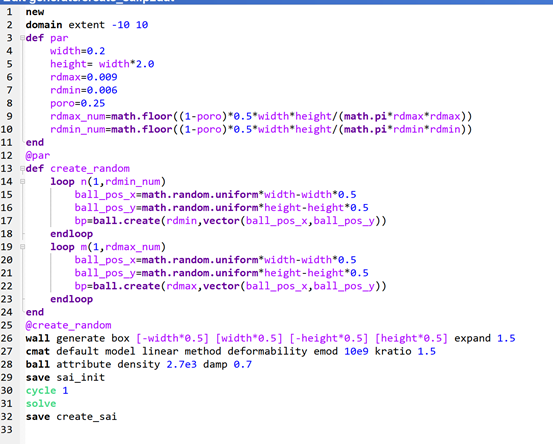
图5.1:“强行塞”代码
在未平衡前,式样状态为:
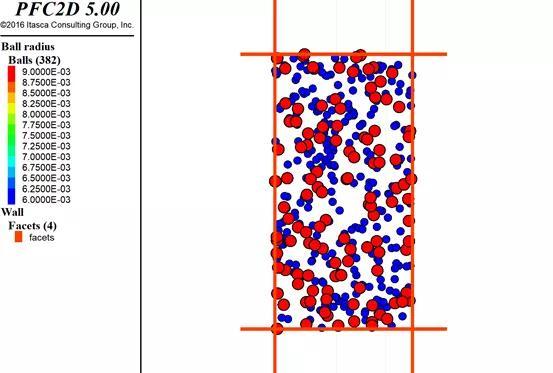
图5.2:“强行塞”平衡前
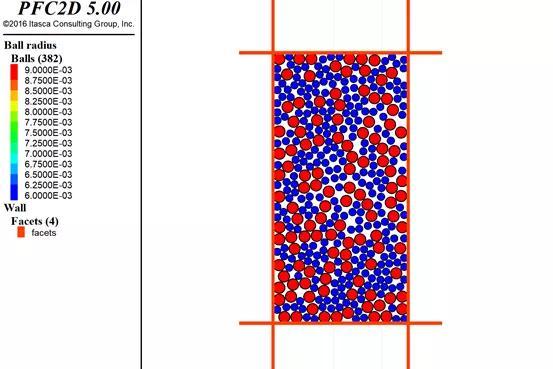
图5.2:“强行塞”平衡后
到这里可能很多同学已经发现了,这个形成方法不就是ditribute吗?是的没错,distribute正是基于这样的思路建立起来的,下一节我们就介绍一下ditribute的用法。
六、指定级配孔隙率的成样方法——distribute
distribute方法是专门用来生成级配式样的,就目前来看可以说是最便捷的方法了。下面我们就使用distribute来生成我们上面的式样。这个方法用的人比较多了,就不去叙述了。
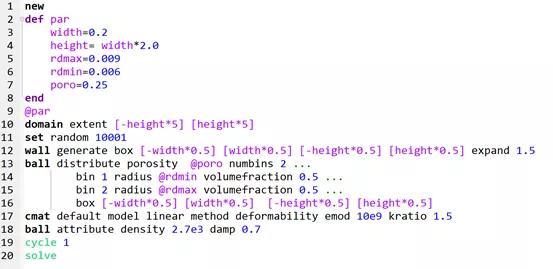

图6.1:distribute成样代码和模型
下面我们讲一下distribute 的进阶,distribute在颗粒数比较多的时候,效果不是很好,会因为颗粒分布不均匀导致的不均匀性。为了克服这个缺点,有学者引入了GM法,这个方法是用网格的形式去生成颗粒,代码如下,这里不去过多的讲解,可以参考一下相关的文献。

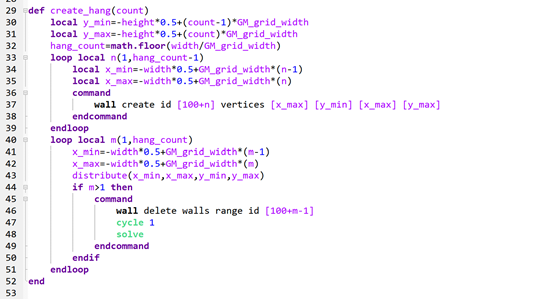


图6.3:GM法结果模型
可以发现这个方法生成的颗粒数比预想的要低,这是因为我这里颗粒数比较少,在生成的时候产生了较大的误差。
到这里又熟悉了,想到了PFC中的Brick方法。
七、超级快速的大模型成样方法——Brick
就像其意思一样,Brick方法是先生成满足条件的一个小块,然后用这个小块拼凑起整个模型。这个东西牛逼的是计算速度,上面的分层法计算一次基本上都需要十几分钟左右,但是brick方法只需要1秒!
Brick分为两部分:
(1)首先生成基本的砖头,注意这里的domain必须是周期边界,并且大小就是砖头的大小
(2)之后利用brick关键词进行组装
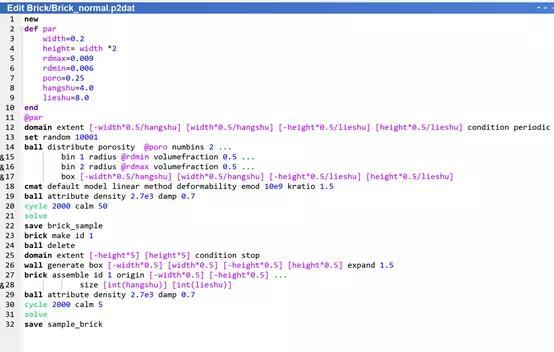

图7.2:一个Brick
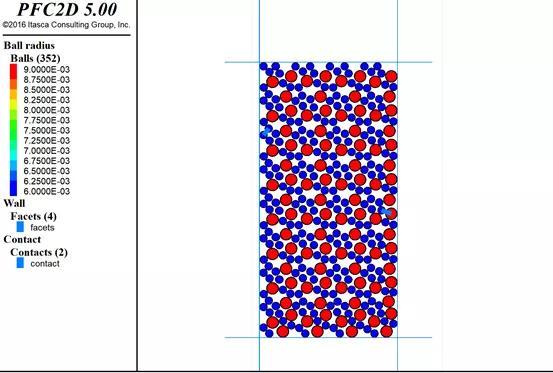
图7.3:组装完成后的Brick
可以发现Brick方法是对一部分可以的重复复 制,所以计算量会小很多,我这里的数目比较少,可能效果不是特别好。Brick方法和GM法是类似的,但是GM法在每个网格中都有不一样的随机数,这样不会产生Brick方法中鱼鳞状的效果,我认为相较于Brick方法,可能GM法更加适用于我们的岩土类材料。
八、写在最后
以上便是我总结出来的PFC成样方法了,从底层到顶层都过了一遍,但是我这里只使用了两个粒径,对于多粒径的方法读者可以在理解后自行扩充,distribute相关的方法还是比较容易的,generate相关的方法各位还是得费点心思。
为了帮助大家掌握离散元颗粒生成的基本概念,接触不同的成样方法以及相关代码编写,4月24日20时,我将在仿真秀官网和App视频直播《岩土离散元·PFC案例课堂 第二讲:PFC成样方法详解》,希望对PFC初学者和使用PFC的理工科院校硕博士(尤其是PFC交流群的道友)有些许些许帮助。我的直播分享内容如下:
最原始的成样——Create 无重叠的成样方法——generate 指定空间”的解决办法——压缩法、分层压缩、UCM法 “指定粒径“的解决办法——粒径膨胀法 “指定数目“的解决办法——“强行塞” 指定级配孔隙率的成样方法——distribute、GM法 超级快速的大模型成样方法——Brick 互动答疑 福利派发
如何听课(点击下图可以观看和回看直播)
识别下方二维码即可永久反复收看,文章中所有代码仅对参加直播的同学免费开放,且直播前分享海报到朋友圈可领取,直播结束后凭分享截图,联系仿真小助手领取。希望进入PFC软件交流群朋友注意,进群人数大于200人请添加任意仿真小助手(fangzhenxiu999),人工邀请加入Lobby老师的 用户交流群。






