OpenFOAM|20 自定义边界条件
- 作者优秀
- 优秀教师/意见领袖/博士学历/特邀专家
- 平台推荐
- 内容稀缺
本文摘要(由AI生成):
文章主要介绍了在OpenFOAM中实现自定义边界条件的三种方法:codeStream、高层编程和外部程序库。其中,codeStream是最简单的方法,大多数情况下都可以使用其对边界条件进行编码。高层编程需要更深入的了解C和OpenFOAM API。利用swak4foam可以生成外部程序库,但作者对此了解不多。文章还通过几个简单的例子介绍了如何使用codeStream实现二维和三维空间分布的边界条件。
OpenFOAM中虽然提供了许多不同类型的边界条件,但有些特殊的边界类型可能还是无法实现(如指定某边界上随时空分布的物理量)。好在OpenFOAM允许用户自定义边界条件,因此理论上可以指定任意形式的边界条件。要实现自己的边界条件,可以采用三种方式:codeStream、高层编程(High level programing)、外部程序库(如swak4foam)。
codeStream是实现自定义边界条件的最简单方法,大多数情况下用户都可以使用其对边界条件进行编码。如果一些边界条件无法使用codeStream实现,此时可以使用高层编程(即编程开发一个新的边界条件类型),当然这需要对C 和OpenFOAM API有更深入的了解。
对于利用swak4foam,有兴趣的道友可以自行查阅相关资料,我对其了解不多。
1 利用codeStream实现边界条件
OpenFOAM能够在运行时编译、加载并执行C 代码。利用指令#codeStream可以实现此此功能。
该指令可在任何输入文件中用于运行时编译 此伪指令读取条目 code(必选),codeInclude(可选),codeOptions(可选)和codeLibs(可选),并使用它们生成动态代码源代码在运行时自动编译,自动生成源代码和二进制文件,并且复 制到当前算例目录 dynamicCode中对于简单的边界条件,使用 codeStream是避免对边界条件进行高级编程或使用外部库的一种很好的选择codeStream可以在任何字典文件中使用
注:codeStream有点类似Fluent UDF中的DEFINE_PROFILE宏,在不惊动求解器内核的前提下使用编程的方式实现边界条件上物理场分布的自定义。
”
下面是一个codeStream应用代码片段:
// 边界名称
patch-name
{
// 数值边界类型为fixedValue
type fixedValue;
// 指定边界值采用codeStream进行指定
value #codeStream
{
// 下面插入编译所需的头文件
// 多数情况下需要包含fvCFD.H
codeInclude
#{
#include "fvCFD.H"
#};
// 这里插入编译选项
// 多数情况下如下所示保持不变
codeOptions
#{
-I$(LIB_SRC)/finiteVolume/lnInclude \
-I$(LIB_SRC)/meshTools/lnInclude
#};
// 这里插入编译所需的库
// 多数情况下如下所示
codeLibs
#{
-lmeshTools \
-lfiniteVolume
#};
// 这里插入源代码
code
#{
#};
};
}
大多数情况下只需要按上面的框架,填充code下面的内容即可。
2 codeStream例子
下面用几个简单的例子来描述这一过程。
2.1 二维空间分布
如下需要在下图所示的计算模型中指定入口边界velocity-inlet-5的速度沿Y方向成抛物线分布。
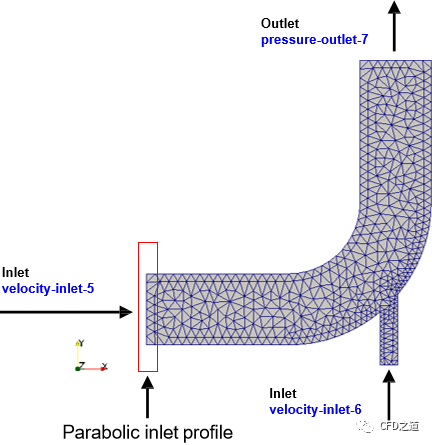

code
#{
// 这里进入到case路径下
const IOdictionary& d = static_cast<const IOdictionary&>
(
dict.parent().parent()
);
// 访问网格数据
const fvMesh& mesh = refCast<const fvMesh>(d.db());
// 在网格数据中找到边界velocity-inlet-5的id
const label id = mesh.boundary().findPatchID("velocity-inlet-5");
// 利用边界id访问边界网格信息
const fvPatch& patch = mesh.boundary()[id];
// 初始化向量场,这个向量场用于为边界赋值
vectorField U(patch.size(), vector(0, 0, 0));
...
...
...
#};
这里的代码除了边界名称外,其他的基本不用修改。信息准备完毕后即可利用程序代码实现边界分布。
如本算例,可以采用下面的代码:
code
#{
// 这里定义公式中需要的常量
const scalar pi = constant::mathematical::pi;
const scalar U_0 = 2.;
const scalar p_ctr = 8.;
const scalar p_r = 8.;
// 循环访问边界上的所有网格面
// 这里等效于for (int i=0;i<patch.size();i )
forAll(U, i)
{
// 获得网格的y坐标
const scalar y = patch.Cf()[i][1];
// 给每一个网格指定其速度向量
U[i] = vector(U_0*(1-(pow(y - p_ctr,2))/(p_r*p_r)), 0., 0.);
}
// 将U值写入到字典中
writeEntry(os, "", U);
#};
计算结果完毕后的速度分布如下图所示。
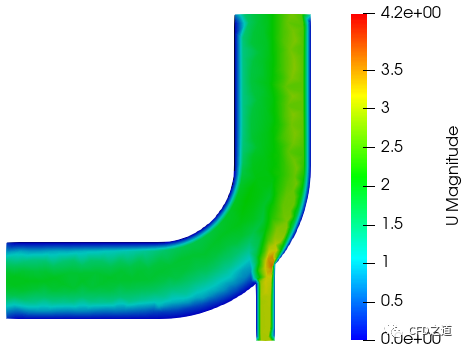
边界velocity-inlet-5上速度分布如下图所示。速度在空间上成抛物线分布,与前面预设的保持一致。
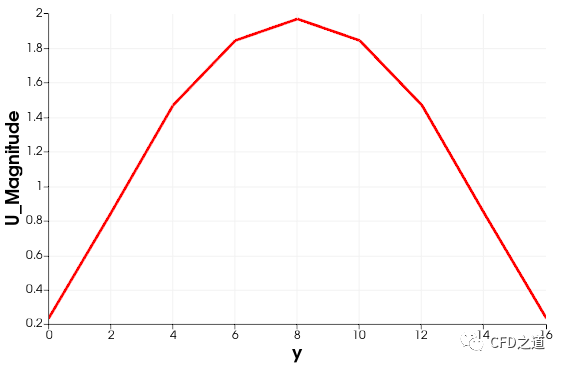
2.2 三维空间分布
如下面的三维模型。
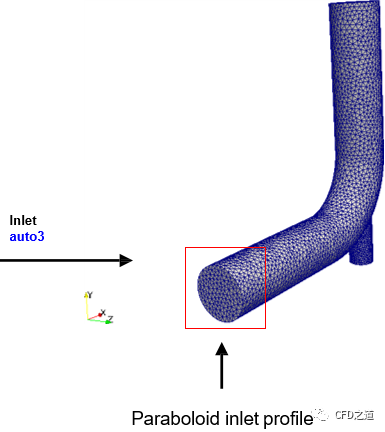
要指定入口边界auto3的速度分布为:
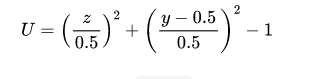
这个其实和前面二维模型可以一样处理。code中程序代码如下所示:
code
#{
...
...
...
vectorField U(patch.size(), vector(0, 0, 0) );
const scalar s = 0.5;
forAll(U, i)
{
// 先得到x、y、z的坐标值,然后将函数规律写入字典
const scalar x = patch.Cf()[i][0];
const scalar y = patch.Cf()[i][1];
const scalar z = patch.Cf()[i][2];
U[i] = vector((pow(z/s, 2) pow((y-s)/s,2) - 1.0), 0, 0);
}
writeEntry(os, "", U);
#};
3 codedFixedValue边界
OpenFOAM中还可以使用边界条件codeFixedValue,该边界条件由codeStream派生而来,可以采取与codeStream类似的方式工作。codedFixedValue边界使用起来更友好,且允许访问仿真数据库的更多信息(如可以访问时间信息)。这些边界条件还可以从可运行时修改的外部字典(system/codeDict)中读取代码。
另一种边界条件codedMixed与codedFixedValue工作方式类似,此边界条件可以访问固定值(Dirichlet BC)和梯度值(Neumann BC)。
下面使用codedFixedValue实现抛物线速度分布。
// 边界名称
patch-name
{
// 指定类型为codeFixedValue
type codedFixedValue;
// 指定边界初始值
value uniform (0 0 0);
// 指定的名称标识符
name name_of_BC;
// 编译时所需的信息,按实际需求给
codeOptions
#{
-I$(LIB_SRC)/finiteVolume/lnInclude \
-I$(LIB_SRC)/meshTools/lnInclude
#};
codeInclude
#{
#include "fvCFD.H"
#include <cmath>
#include <iostream>
#};
code
#{
// 下面三行为标准写法,一般不用修改
const fvPatch& boundaryPatch = patch();
const vectorField& Cf = boundaryPatch.Cf();
vectorField& field = *this;
scalar U_0 = 2, p_ctr = 8, p_r = 8;
forAll(Cf, faceI)
{
field[faceI] = vector(U_0*(1-(pow(Cf[faceI].y()-p_ctr,2))/(p_r*p_r)),0,0);
}
#};
}
可以看到,codeFixedValue的写法要比codeStream简洁得多。在实际应用过程中可以将其作为模板,只需要根据实际边界条件修改代码部分。根据所编写的程序代码,可能需要添加新的头文件和编译选项。需要注意,如果当前使用向量,则需要使用向量场。而如果使用标量,则需要使用标量场。使用这些边界条件的一个缺点是无法查看零时刻的物理场分布,需要至少仿真迭代一次。这些边界条件最大的好处是可以从仿真数据库中仿真时间。可以通过添加以下语句访问时间:
this -> db().time.value()
如下面构造一个与时间相关的边界条件:
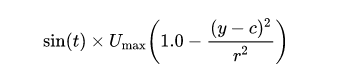
可以采用下面的程序代码:
code
#{
const fvPatch& boundaryPatch = patch();
const vectorField& Cf = boundaryPatch.Cf();
vectorField& field = *this;
scalar U_0 = 2, p_ctr = 8, p_r = 8;
// 得到时间
scalar t = this->db().time().value();
forAll(Cf, faceI)
{
field[faceI] = vector(sin(t)*U_0*(1-(pow(Cf[faceI].y()-p_ctr,2))/(p_r*p_r))),0,0);
}
#};
4 codedFixedValue例子
这里举一个使用codedFixedValue同时处理标量场与矢量场的例子。
如下面的计算模型,需要为图中深色位置指定速度场(矢量)与体积分数(标量)。简单起见,这里只展示代码部分。
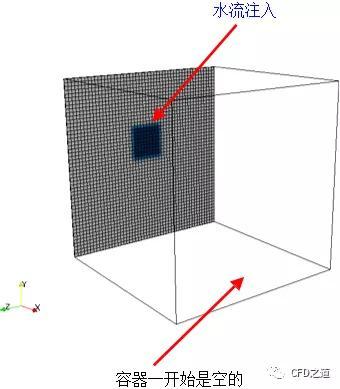
在0/U文件中指定速度场:
leftWall
{
type codedFixedValue;
value uniform (0 0 0);
name inletProfile1;
code
#{
const fvPatch& boundaryPatch = patch();
const vectorField& Cf = boundaryPatch.Cf();
vectorField& field = *this;
scalar minz = 0.4;
scalar maxz = 0.6;
scalar miny = 0.5;
scalar maxy = 0.7;
scalar t = this->db().time().value();
forAll(Cf, faceI)
{
if ((Cf[faceI].z() > minz) &&
(Cf[faceI].z() < maxz) &&
(Cf[faceI].y() > miny) &&
(Cf[faceI].y() < maxy))
{
if ( t < 1.)
{
field[faceI] = vector(1,0,0);
}
else
{
field[faceI] = vector(0,0,0);
}
}
}
#};
}
在alpha.water文件中指定边界上水相的体积分数:
leftWall
{
type codedFixedValue;
value uniform 0;
Name inletProfile2;
code
#{
const fvPatch &boundaryPatch = patch();
const vectorField &Cf = boundaryPatch.Cf();
scalarField &field = *this;
field = patchInternalField();
scalar minz = 0.4;
scalar maxz = 0.6;
scalar miny = 0.5;
scalar maxy = 0.7;
scalar t = this->db().time().value();
forAll(Cf, faceI)
{
if (
(Cf[faceI].z() > minz) &&
(Cf[faceI].z() < maxz) &&
(Cf[faceI].y() > miny) &&
(Cf[faceI].y() < maxy))
{
if (t < 1.)
{
field[faceI] = 1.;
}
else
{
field[faceI] = 0.;
}
}
}
#};
}
具体就不详细解释了,其实很容易读懂。
声明:原创文章,欢迎留言与我讨论,如需转载留言






