热导方程的Matlab数值解方法

这是一个很久很久以前的一个故事,久到能够让人忘记原来这这些方程是如此的贴近自己的学习。你学或者不学,它都在这里,不难也不简单。过冷水今天就和大家分享一下一维热传导方程特别案例的具体求解方法。
热传导是一个很常见的现象。当物体内部的温度分布不均匀时,热量就会从温度较高的地方流动,这个过程中,温度是空间和时间的函数。热传导方程就是温度所满足的偏微分方程,它的解给出任意时刻物体内的温度分布。
为了建立热导方程,我们首先介绍热导系统置于x轴,考查系统在任意x处的横截面上的一个单位面积,设热流沿x轴方向传递,x处的温度为u(x),温度梯度为du(x)/dx。傅里叶指出:在单位面积内流经该单位面积的热量q与该处的温度梯度成正比即:
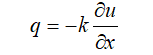
k:热导率,负号表示与温度梯度方向相反。现在假设这个一维热传导系统的长度为l,横截面面积为s杆的两个端点处于x=0和x=l.假定杆在初始t=0时刻温度分布为Φ(x),在随后的时间(t>0),热量在杆中流动。现在我们要确定在任意t时刻,杆中任意位置x(0<x<l)的温度u(x,t)。
我们考查系统在x位置的一段∆x,根据傅里叶定律在∆t时间内从∆x前端流入的热量为:
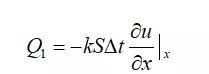
另一方面,在该时间内从后端流出的热量为:
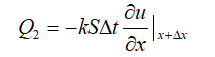
在没有其他热源的情况下,体积元S∆x吸收的热量使之温度升高。而温度升高的描述则是基于热体比热c的定义:
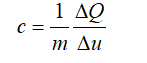
其中,m是物体的质量,c表示单位质量的物体温度升高1K所需要的热量。这样体积元S∆x吸收的热量为:
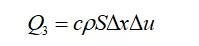
其中,ρ=m/(S∆x)是系统质量体密度。热量守恒要求:
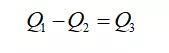
则:
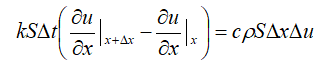
对其进行进一步变化可得:
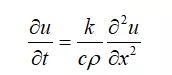
这就是所谓的一维系统的热传导方程。我们对热传导方程进行一个简单的分析,若时间的微商项du(x)/dt=0这是稳态过程。则d2u(x)/dx2=0则:
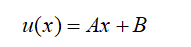
有热源的热传导方程为:
我们来看一个比较简单形式的求解方法。
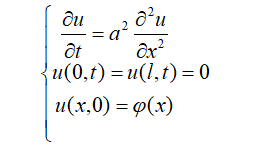
该条件下的热导方程求解,采用两种不同的形式分离变量法和差分法。我们先来看分离变量法:
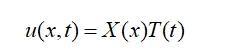
则:
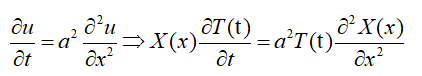
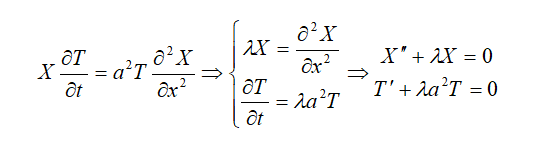
由边界条件u(0,t)=0,u(l,t)=0可得X(0)=X(l)=0,求边值问题:
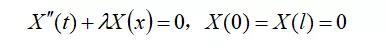
解:
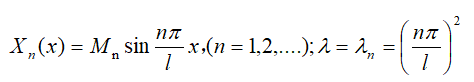
这里需要解释一下X、、(x) λX(x)=0微分方程根据λ<0,λ=0,λ>0;表示成不同函数类型,除λ>0能够得到符合边界条件的函数外,其它都不符合边界条件。
现在考虑:
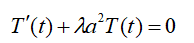
将特征值λ带入方程的:
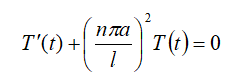
通解为:
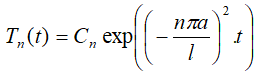
于是:
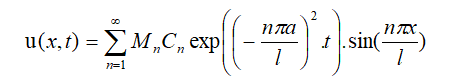
再利用初值条件:u(x,0)=φ(x)可得:
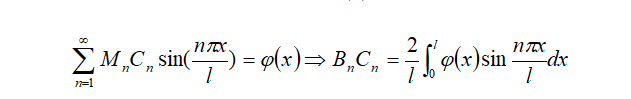
于是最终解就是给出来:
我们看一道有具体条件的题:
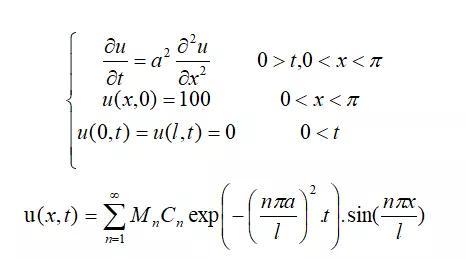
再利用初值条件:u(x,0)=φ(x)可得:
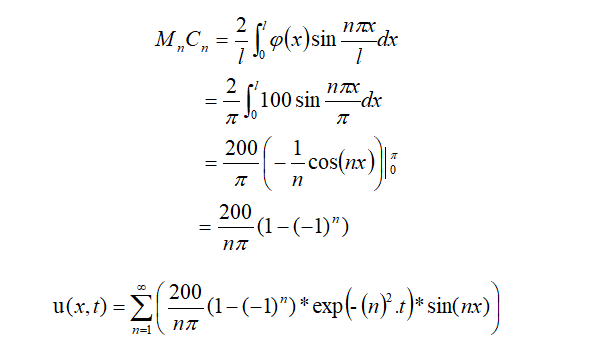
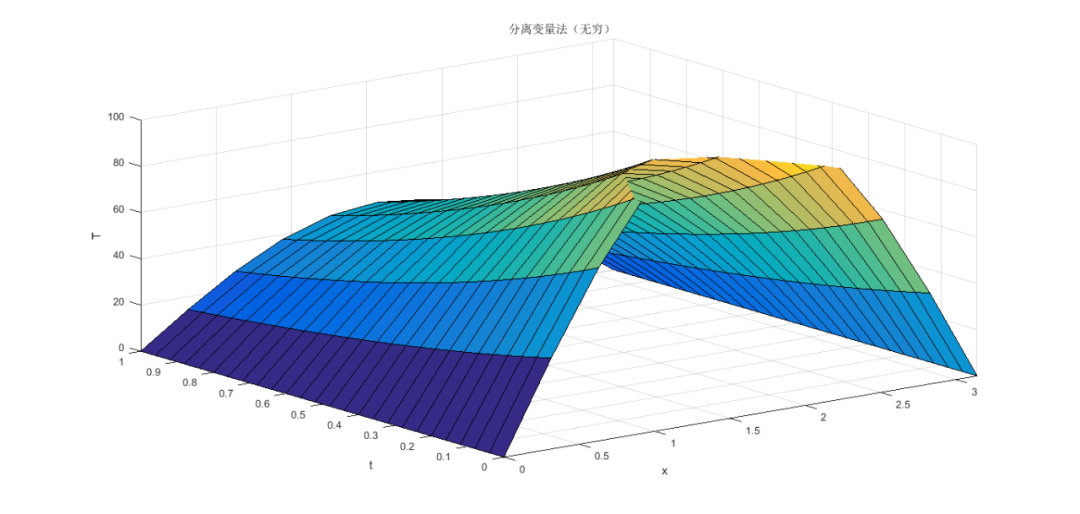
最终结果有没有觉得神秘复杂的热导方程好像也不是那么难计算,就是一个累计加和的形式,很简单。读者需要注意的是热导方程的形式是和边界条件有关系的,不同的边界条件最终的形式差别是很大的,我们来看一下代码:

热导方程的数值解代码出乎意料的简洁。我们再来看一下另外一种求解方法:有限差分方法。
有限差分:将求解域划分为差分网格,用有限个网格节点代替连续的求解域。有限差分方法以泰勒级数展开等方法,把控制方程中的导数用网格节点上函数值的差商代替进行离散,从而建立以网格节点上的值为未知数的代数方程组.
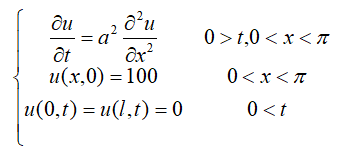
离散化:
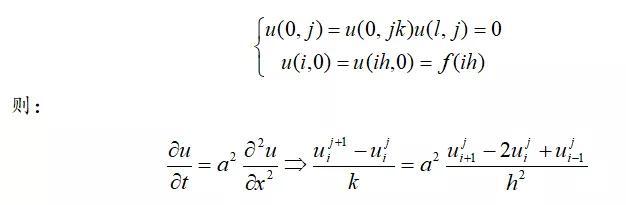
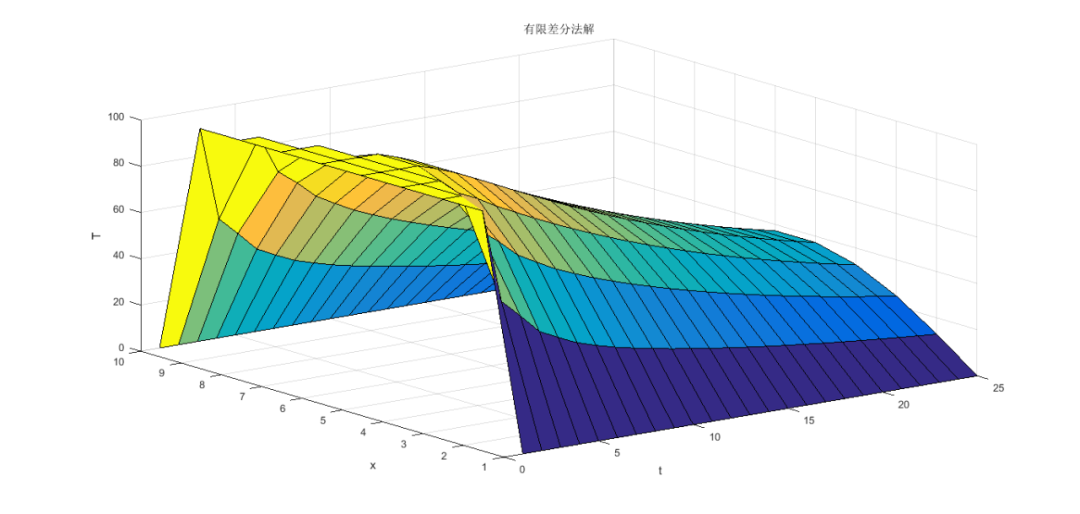
其代码实现为:

这就是过冷书想要和大家分享的关于一维热传导方程求解的方法,数值解的代码过程很简单,主要是数学问题,第一种方法用到了分离变量的思想使得温度变得简单。第二种方法就是用具体值来近似表示热导方程。使得问题变得简单。看完之后才有豁然开朗的感觉,数学也没有想象中的那么难。限于篇幅一部分人所关注的二维热传导方程敬请起来后期会和大家分享二维热导方程案例,具体实现代码。
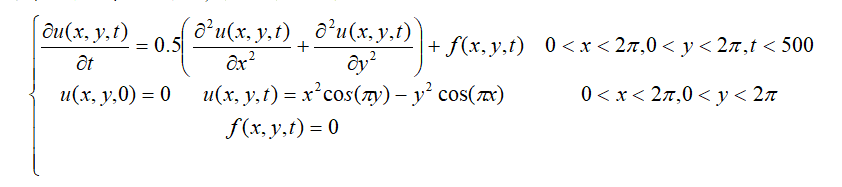
原创文章,作者过冷水,未经授权,禁止私自转载,转载请联系作者,如果您希望加入Matlab仿真秀官方交流群和资料下载可加群:927550334
精品回顾>>>>>>