力学分析:滞弹性与材料内耗
来源:力学酒吧微信公众号(ID:Mechanics-Bar),作者:张伟伟。
弹性变形是指物体在外力作用下发生变形,去除外力之后,物体完全恢复原来的形状和尺寸的性质。在材料力学和弹性力学中,认为弹性变形具有单值性,一个载荷唯一的对应一种变形;可逆性,材料总能完全恢复到原来的状态;瞬时性,加载时材料立即变形,卸载后又立即恢复原状,变形和时间无关,加载曲线和卸载曲线完全重合。这被称为理想弹性变形,或者说弹性变形是完整的。
然而,对于大多数金属材料,往往具有多晶、微观缺陷等特性,这将导致材料在发生弹性变形时并不是完整的,不再满足理想弹性变形的单值性、可逆性和瞬时性。
1825年,德国物理学家Wilhelm Eduard Weber (1804-1891) 在研究电流计悬线时发现,撤去对悬线施加的力偶之后,悬线变形并没有立即回到零点,而是缓慢的、逐渐回到零点(相对于载荷存在延迟)。1848年,美国物理学家Clarence Melvin Zener (1905-1993) 首先给出了滞弹性 (anelasticity) 的概念来描述材料变形的这种性质。
滞弹性表明真实材料在发生弹性变形,应变不仅是应力的函数(随应力变化),同时还是时间的函数(随时间变化)。如图1所示,对材料施加σ0,假定对于理想弹性变形,加载和卸载将沿着OB进行。但当材料为滞弹性时,材料加载时并不是直接从O点到达B点,而是先从O点加载到A点,然后材料保持应力不变,应变缓慢的增加,到达B点,加载曲线为OAB。卸载时,材料也不能直接从B点直接到达O点,而是先从B点卸载到c点,然后再经过一些时间,从c点到达O点。这种应变落后于应力的现象也称为弹性后效,加载和卸载时出现弹性后效分别为正弹性后效和反弹性后效。
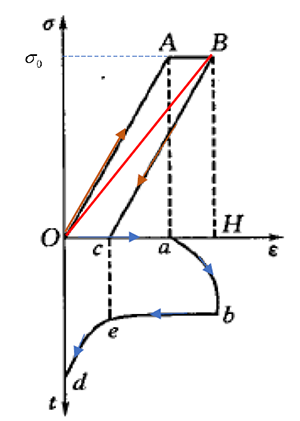
图1 滞弹性变形示意图
从弹性变形的定义来看,材料经过加载产生变形,卸载后变形完全恢复,属于弹性变形。但由于变形过程中,应变滞后于应力,并和时间有关。因此,这种弹性变形被称为滞弹性。
从图1的下半部分来看(可想象逆时针旋转90度观察),加载时的Oa段和卸载时的be段,应变不随时间而变化,称为瞬时弹性应变;而加载时的ab段和卸载时的ed段,应变都是时间的函数。满足“应力保持不变,应变发生缓慢变化”的蠕变特性,因此ab段和ed段也被称为弹性蠕变,它们分别对应于正弹性后效和反弹性后效。
弹性后效在仪器仪表和精密机械制造中极为重要,例如一些重要的传感器元件(如测力弹簧、薄膜传感器)在使用过程中就必须考虑弹性后效,否则测量结果将会出现误差。在金属冶炼中,通过回火等热处理工艺可使得材料组织结构更加稳定,尽量消除弹性后效产生的应变。
将加载曲线和卸载曲线统一起来看,OABO构成一个封闭环,称为弹性滞后环,其面积正比于材料在加载、卸载过程中的能量损耗。记加载段外力做功(材料储存的弹性势能)为W1,大小正比于OABH的面积,有
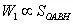
而卸载时,弹性势能释正比于BHc的面积,有
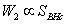
显然,SBHc<SOABH,从加载到卸载,能量损耗为SABcO,也就是说即便在弹性范围内,材料的加载和卸载也将发生能量损耗,称为内耗 (internal friction)。我们常见物体发生自由振动时,幅值会逐渐衰减直至静止,固体中传播的声波会逐渐衰减直至消失,这都是材料内耗的结果。
材料内耗的机理比较复杂,材料物理学家从不同的角度提出了多种理论。如热弹性内耗理论,认为材料在动态加载过程中,材料局部因受力发生绝热升、降温,从而产生内耗,这种内耗与加载频率直接相关。又从晶体角度考虑,滞弹性内耗是由晶界热弹性、晶界滑移、晶界散射等引起的。再如从磁弹性角度看,应力作用下物质会发生磁化从而引起能量损耗。又或者从组成材料的微粒看,不同原子、位错、缺陷等因素在受力时会发生位置重排,这也会导致内耗。
与材料物理学家不同,力学家忽略材料的微观组织,从唯象理论出发,利用弹簧和黏壶的串联、并联模型来解释材料的滞弹性。如图2所示,当弹簧和黏壶为并联关系时,被称为Voigt模型;当弹簧和黏壶为串联时,被称为Maxwell模型。该模型中由于存在黏壶,变形与时间有关(黏壶产生的阻力与速度相关),可用来模型滞弹性变形。
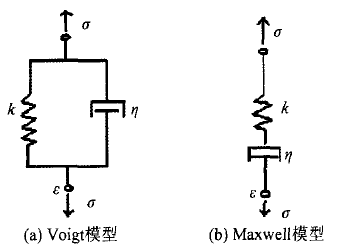
图2 弹簧和黏壶并联、串联模型
来源:《固体低频内耗力学模型及其测量研究》
给出滞弹性概念的美国物理学家Zener提出了Zener模型来描述滞弹性变形,实际可视为三参量的Maxwell模型。
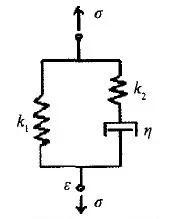
图3 Zener模型
来源:https://wenku.baidu.com/view/49d91c3e376baf1ffc4fad19.html
为了标定不同材料能量损耗的特性,人们用载荷循环一周内的相对能量损耗再除以2π来定义材料内耗值,即
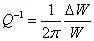
这里,Q-1表示内耗值,ΔW 表示一个循环内能量损耗,W 表示一个循环内外力所做的功。材料内耗值的测定方法有强迫振动法、自由衰减法和波传播法等。强迫振动法是指,对试样施加一个交变载荷,可以通过应变落后于应力的相位角来确定材料的内耗值。满足关系式
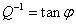
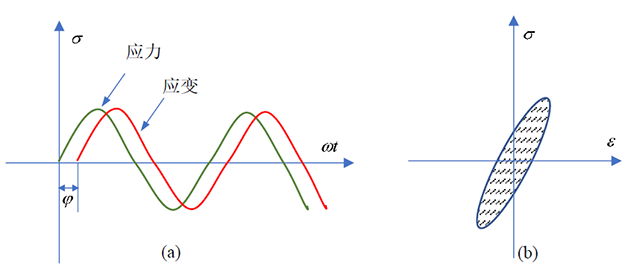
图4 强迫法测定材料内耗
自由衰减法是将试件振动激发后,任其自由振动,其振动曲线如图5所示,内耗表示为
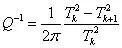
其中,TkTk 1 为相邻振幅大小。
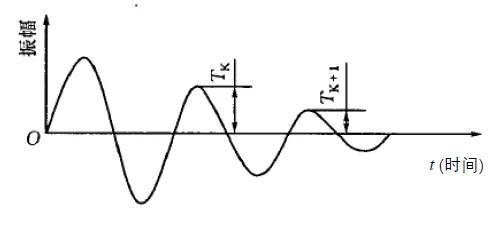
图5 自由振动衰减曲线
波传播法利用弹性波在传播过程中的衰减测定材料的内耗值,其表达式为

其中,v 表示弹性波的波速,f 表示频率,α 表示传播单位长度的对数衰减量。
内耗表征了材料内部的能量衰减能力,是设计选材的重要指标。例如,对于那些易振但不希望它们发生振动的部件,通常选择内耗值高的材料。汽轮机叶片常用1Cr13钢制造,这种钢不仅具有耐热、高强度的特性,关键还在于它有较高的内耗值,具有良好的消振特性。但对于制作传感器的弹性元件,就希望它们的内耗值越小越好。如果弹性元件的内耗值大,弹性元件则会将试样的一部分能量转变为内耗,从而引起测量误差,并降低了传感器的灵敏度。因此,选用内耗值小的材料制作弹性元件,可有效提高传感器的灵敏度和测量精度。
参考文献:
[1] 王磊. 材料的力学性能. 东北大学出版社. 2007
[2] 周正存等. 固体低频内耗力学模型及其测量研究. 苏州市职业大学学报. 2013
[3] 材料的滞弹性与内耗.
https://wenku.baidu.com/view/859a22f00029bd64783e2c9f.html
[4] 粘弹性和滞弹性
https://wenku.baidu.com/view/49d91c3e376baf1ffc4fad19.html
[5] 内耗的分类、特点及其与金属结构的关系.
http://www.360doc.com/content/17/0731/00/27479324_675462046.shtml





