ANSYS之DPC模型的钢筋混凝土周边简支板极限承载力分析
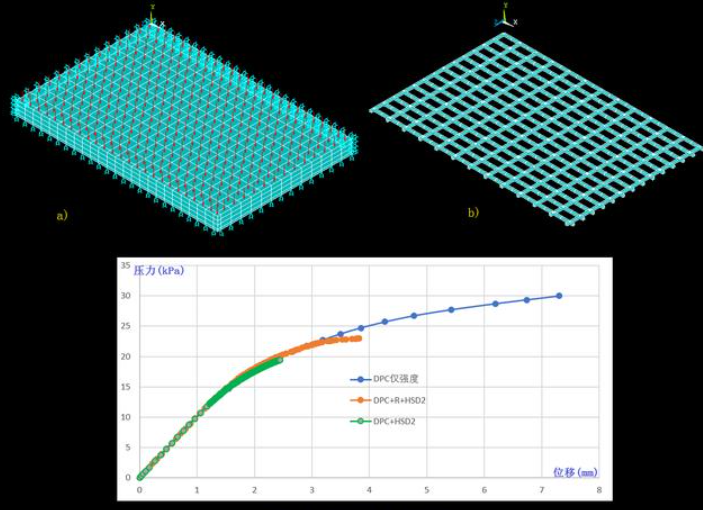
设钢筋混凝土板尺寸为6m×4m×0.2m,不计自重,分析在均布压力作用下的极限承载力。根据对称性,取1/4模型进行分析,如图1a)所示。
建模时,假定水平钢筋网布置在一层,且其保护层为30mm,钢筋间距分别为0.245m和0.15m,钢筋直径均为6mm,如图1b)所示。
分析采用分离式模型,混凝土采用SOLID185单元,钢筋采用LINK180单元。
混凝土材料和钢筋材料参数详见命令流,此处不再重复。
FINISH$/CLEAR$/PREP7
!几何参数定义
PL=6!板长度
PB=4!板宽度
PD=0.2!板厚度
PBH=0.03!钢筋保护层(中)
!混凝土材料参数-C30混凝土---------
EC=3.0E10!混凝土弹性模量()
BOS=0.2!泊松系数
CDEN=2350!混凝土密度(KG/M^3)
MP,EX,1,EC$MP,PRXY,1,BOS
MP,DENS,1,CDEN
!采用混凝土标准强度
RC=20.1E6!单轴抗压强度
RT=2.01E6!单轴抗拉强度
RB=1.2*RC!双轴抗压强度
DETC=1.0!压缩剪胀系数
DETT=0.25!拉伸剪胀系数
TB,CONCR,1,,,DP
TBDATA,1,RC,RT,RB
TB,CONCR,1,,,DILA
TBDATA,1,DETT,DETC
!tb,concr,1,,,rcut
!tbdata,1,rt
!采用HSD2-----------------
OCI=0.3!开始硬化时相对应力
OCU=0.5!与KCU对应的相对应力
OCR=0.25!剩余压缩相对应力
KCM=0.00164!强度峰值点应变
KCU=0.003772!变点应变
OTR=0.15!剩余拉伸相对应力
GFT=115!拉伸比面积断裂能
TB,CONCR,1,,,HSD2
TBDATA,1,KCM,KCU,OCI,OCU,OCR
TBDATA,6,GFT,OTR
!钢筋材料参数-----------------
!设采用HRB400钢筋
MP,EX,2,2.1E11!钢筋弹性模量
MP,PRXY,2,0.3$MP,DENS,2,7850
TB,BKIN,2!双线性随动强化模型
TBDATA,1,400E6,1600E6
!创建模型--离散钢筋模型-------
BLOCK,0,PL/2,-PD,0,0,PB/2
!直径为6MM的钢筋面积
AG6=ACOS(-1)/4*6E-3*6E-3
DX=0.245!X向钢筋间距
DZ=0.15!Z向钢筋间距
*DO,I,1,13$WPOFF,,,DZ
VSBW,ALL$*ENDDO
WPCSYS,-1$WPRORA,,,90
*DO,I,1,12$WPOFF,,,DX
VSBW,ALL$*ENDDO!
WPCSYS,-1$WPROTA,,90
WPOFF,,,PD-PBH$VSBW,ALL
ET,1,SOLID185,,3
VATT,1,1,1$MSHKEY,1
LSEL,S,TAN1,X$LSEL,R,TAN1,Z
LSEL,U,LOC,Y,-PD,-(PD-PBH)
LESIZE,ALL,,,3
LSEL,ALL$ESIZE,0.15
VMESH,ALL
!钢筋划分
!X方向钢筋的MESH200---------
ET,2,LINK180
SECTYPE,2,LINK$SECDATA,AG
LSEL,S,LOC,Y,-(PD-PBH)
LSEL,U,LOC,X,PL/2
LSEL,U,LOC,Z,PB/2
LATT,2,,2,,,,2
LMESH,ALL$ALLSEL,ALL
!修改边界上的混凝土单元为弹性单元
MP,EX,3,EC$MP,PRXY,3,BOS
MP,DENS,3,CDEN
NSEL,S,LOC,X,PL/2
NSEL,A,LOC,Z,PB/2$ESLN
ESEL,R,ENAME,,SOLID185
EMODIF,ALL,MAT,3$ALLSEL,ALL
!施加边界条件
!竖向约束
NSEL,S,LOC,X,PL/2!
NSEL,R,LOC,Y,-PD$D,ALL,UY
NSEL,S,LOC,Z,PB/2
NSEL,R,LOC,Y,-PD$D,ALL,UY!
!对称约束
NSEL,S,LOC,X$D,ALL,UX
NSEL,S,LOC,Z$D,ALL,UZ
ALLSEL,ALL
!施加荷载求解
/SOLU
AUTOTS,ON$OUTRES,ALL,ALL
ERESX,NO$P0=30E3$TIME,1
NSEL,S,LOC,Y
SF,ALL,PRES,P0$NSEL,ALL
NSUBST,100,,30$SOLVE
/POST26
N1=NODE(0,0,-PD)
NSOL,2,N1,U,Y
PROD,3,2,,,,,,-1000
PROD,4,1,,,,,,P0/1000
XVAR,3$PLVAR,4
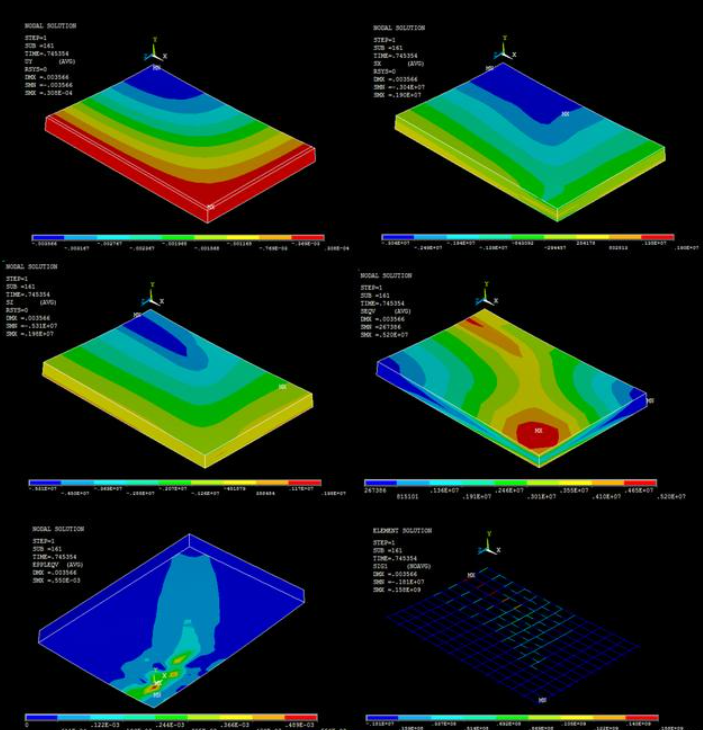
分别采用DPC仅强度、DPC RanKine HSD2、DPC HSD2计算的荷载-位移曲线如图1c)所示,而DPC RanKine HSD2的结果应力云图如图2所示。
采用DPC RanKine HSD2模型,改变钢筋直径(仅仅改变直径,不考虑间距、配筋率、保护层等是否合理)进行了四种情况分析,结果如图3所示。
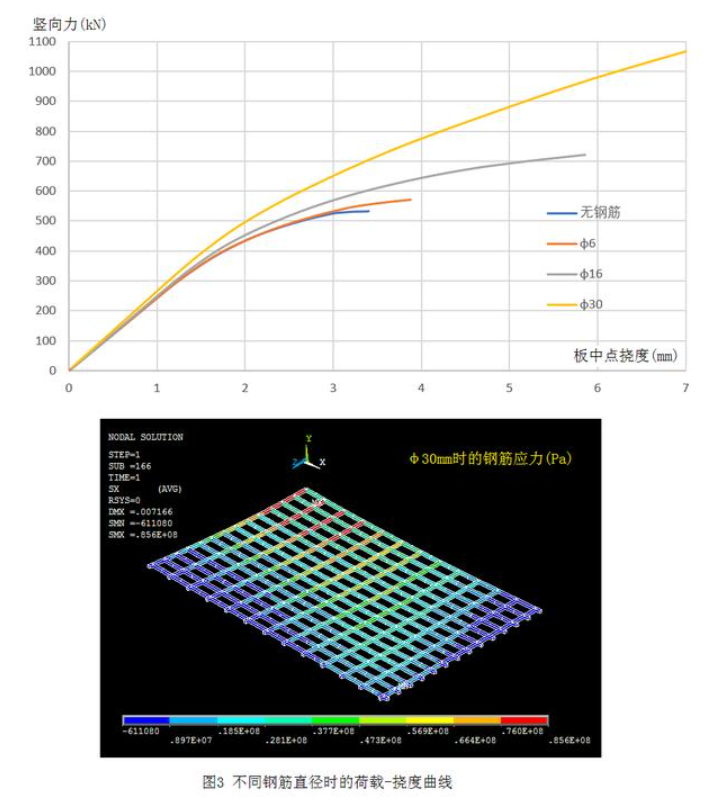
从图中可以看出,素混凝土时也有基本承载力(约530kN),随着钢筋直径的增大,强度和延性逐渐提高。而φ6mm的承载力提高约为8%左右(大约570kN),也就是说相比有钢筋而言,DPC RanKine HSD2模型无筋时也有不低的承载力,或许与HSD2参数有关(可进行参数分析确定是否如此)。
声明:原创文章,欢迎留言与我讨论,如需转载留言