EMD——经验模态分解
来源:CAE 进行时微信公众号(ID:gh_bbbde3e9698b)
经验模态分解 (Empirical Mode Decomposition, 简称EMD) 方法被认为是2000年来以傅立叶变换为基础的线性和稳态频谱分析的一个重大突破,该方法是依据数据自身的时间尺度特征来进行信号分解,无须预先设定任何基函数。正是这样的特性,使EMD 方法在理论上可以应用于任何类型的信号的分解,因而在处理非平稳及非线性数据上,具有非常明显的优势,适合于分析非线性、非平稳信号序列,具有很高的信噪比。
EMD克服了基函数无自适应性的问题。小波分析是需要选定某一个小波基的,小波基的选择对整个小波分析的结果影响很大,一旦确定,在整个分析过程中将无法更换,即使该小波基在全局可能是最佳的,但在某些局部可能并不是,所以小波分析的基函数缺乏适应性。
用EMD有什么好处呢?对于一段未知信号,不需要做预先分析与研究,就可以直接开始分解。这个方法会自动按照一些固定模式按层次分好,而不需要人为设置和干预。
对数据信号进行EMD分解就是为了获得本征模函数 (IMF)。简单来说,信号是由若干个本征模函数所构成的,本征模函数之间相互重叠,便形成复合信号,而EMD分解的目的就是为了分解出其中本征模函数。
经验模态分解的基本思想:将一个频率不规则的波化为多个单一频率的波 残波的形式。
原波形 = ∑ IMFs 余波
EMD分解方法是基于以下假设条件:
数据至少有两个极值,一个最大值和一个最小值;
数据的局部时域特性是由极值点间的时间尺度唯一确定;
如果数据没有极值点但有拐点,则可以通过对数据微分一次或多次求得极值,然后再通过积分来获得分解结果。
这种方法的本质是通过数据的特征时间尺度来获得本征波动模式,然后分解数据。这种分解过程可以形象地称之为“筛选”过程。
1. 找出原数据序列X(t ) 所有的极大值点,并用三次样条插值函数拟合形成原数据的上包络线。
2. 找出所有的极小值点,并将所有的极小值点通过三次样条插值函数拟合形成数据的下包络线。
3. 上包络线和下包络线的均值记作ml,将原数据序列X(t ) 减去该平均包络ml,得到一个新的数据序列hl:X(t )−ml=hl。
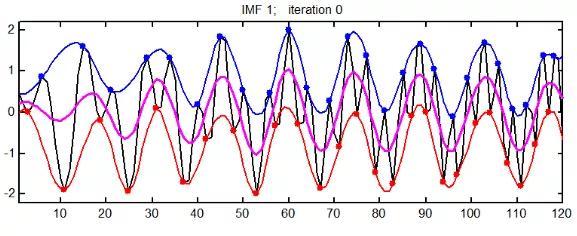
4. 由原数据减去包络平均后的新数据,若还存在负的局部极大值和正的局部极小值,说明这还不是一个本征模函数,需要继续进行“筛选”。筛选条件一是:
在整个数据段内,极值点的个数和过零点的个数必须相等或相差最多不能超过一个;
在任意时刻,由局部极大值点形成的上包络线和由局部极小值点形成的下包络线的平均值为零,即上、下包络线相对于时间轴局部对称。
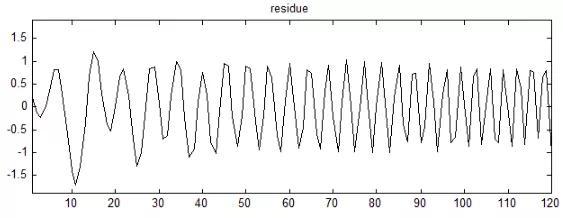
原始信号减均值包络曲线
5. 使用上述方法得到第一个IMF后,用原始信号减IMF1,作为新的原始信号,再通过1~4的分析,可以得到IMF2,以此类推,完成EMD分解。
参考文献:
[1] 知乎专栏与信号处理有关的那些东东 作者Mr.括号
[2] EMD经验模态分解——分析时间序列 作者GerHard_Z
[3] 振动信号处理与数据分析






