ANSYS输出应力、强度理论与规范
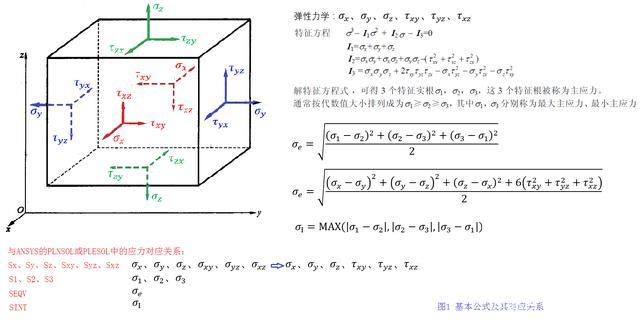
对dx×dy×dz的微小实体,其应力状态如图1所示,并且一点的六个应力分量、三个主拉应力、等效应力、应力密度等公式如图1所示,这些公式在弹性力学中普遍都有介绍(百家号图文无法输入公式,因此只能用图片描述公式,而文本中不得不采用看得懂的方式了)。
而ANSYS实体单元的输出应力包含了六个应力分量SX、SY、SZ、SXY、SYZ和SXZ,三个主应力S1、S2和S3,以及等效应力SEQV和应力强度SINT等,其对应关系如图1所示。
强度理论分为两类,第一类是一脆性断裂为破坏标志的,其中包括最大拉应力理论和最大伸长线应变理论;第二类强度理论是以出现塑性屈服或发生显著塑性变形作为破坏标志的,其中包括最大切应力理论和形状改变能密度理论。
最大拉应力理论-第一强度理论。该理论认为最大拉应力σ1是引起材料脆断破坏的因素,即无论何种应力状态下,只要构件内一点处的主应力中最大的拉应力σ1达到材料强度极限σb,材料就发生脆性断裂。因此第一强度理论的断裂准则是
σ1=σb
考虑安全系数后,就得到以容许应力[σ],因此第一强度理论所建立的强度条件为:
σ1≤[σ]
最大伸长线应变理论-第二强度理论。该理论认为最大伸长线应变是引起材料脆断破坏的因素,即无论何种应力状态下,只要构件内一点处的最大伸长线应变ε1达到材料的极限值εb,材料就发生脆断破坏。因此经过推导后,第二强度理论的断裂准则是
σ1-μ(σ2 σ3)=σb
以容许应力[σ]表示的第二强度理论所建立的强度条件为:
σ1-μ(σ2 σ3)≤[σ]
最大切应力理论-第三强度理论。该理论认为最大切应力τmax引起材料屈服的因素,即无论何种应力状态下,只要构件内一点处的最大切应力τmax达到材料屈服时候的极限值τu,材料就发生屈服。因此经过推导后,第三强度理论的屈服准则是(塑性力学中的特雷斯卡(H.Tresca)屈曲准则)
σ1-σ3=σs
同上,第三强度理论的强度条件是
σ1-σ3≤[σ]
形状改变能密度理论(八面体剪应力理论)-第四强度理论。该理论认为形状改变能密度是引起屈服的因素,即无论何种应力状态下,只要构件内一点处的形状改变能密度达到材料的极限值,该点处的材料就发生屈服。因此经过推导后,第四强度理论的屈服准则是(塑性力学中的冯·米塞斯(Von Mises)屈曲准则)
σe =σs
同上,第四强度理论的强度条件是
σe ≤[σ]
根据这些强度理论,虽然给出了破坏准则或屈服准则,以及强度条件,然而因其适用条件各有不同,因此不能直接用于设计。设计规范也以不同的强度理论为基础,给出了不同的强度条件,这个必然根据设计规范进行。
但根据有限元计算的应力结果如S1/S2/S3、SEQV和SINT,除个别规范的个别条款外,直接用于规范的强度条件的很少。如《钢结构设计标准》(GB50017-2017)铸钢节点应力的强度条件采用的是SEQV。《铁路桥梁钢结构设计规范》还沿用容许应力法,《公路钢结构桥梁设计规范》已改为极限状态法。
因此在不依据某个规范,且用SEQV强度条件时,计算时无荷载系数,可以考虑采用容许应力法,如钢材[σ]= σs/1.7,大致判断设计的可行性;如有荷载及组合系数,可以采用[σ]=设计强度,进行大致判断。通过后,再按具体设计规范严格校核。
---------------------------------------------------------------------------------------------
版权声明:
原创文章,来源铁大王新敏,本文已经授权,欢迎分享,如需转载请联系作者。