该篇,偷个懒,把以前一二三四,集 合在一起,算完结篇吧。经过来回重复的学习以及总结,不敢说真的了解了吧,但是最起码,再看到MOS电容的那些工作区域,没有发怵的感觉了。(1) 不同材料的能带图大概是怎么来的?
如果把绝缘体,半导体,导体三种材料的能带图画在一起的话,大概是这个样子的。带隙Eg大,导带中没有电子,价带中占满电子的是绝缘体;带隙Eg小,导带中没有电子,价带中占满电子的是半导体,这是在T=0K的时候;导带中部分被电子占满,或者导带和价带重叠的,是导体。但是,看到这些能带图的时候,会不会想知道,这到底是怎么来的呢?在量子力学中,电子表现出波粒二象性,所以除了会受到原子核对其的库仑力外,其运动的轨道的周长需要是德布罗意波长的整数倍。这个我把它当成已知条件,虽然我还有十万个为什么,但是我决定不深究了。尽管人生不应该设限,不过还是要有自知之明,要是深究下去,估计我的心力要被耗光了。还是等我心力再足一点,我再来尝试。在上面这些已知条件下,经过一番计算,可以知道这个电子运动的轨道半径r和电子的能量E都是离散的(以下是针对氢原子的推导)。不过呢,这个离散是有条件的,就是需要电子被束缚的情况下,也就是电子的动能不足以克服势能的前提下,即En<0的时候。如果En大于0,即电子为自由电子时,其能量是连续的。所以,当两个氢原子离的很远的时候,电子的能量能级是大概是这样的,他们具有类似的能级。泡利不相容原理说,在一个空间内,不可能有两个电子处于相同的能级。所以当两个氢原子靠的很近的时候,能级就会发生分裂,变成两个挨的很近的能级。而固体中有很多个原子,所以很多离散的能级凑在一块,就变成能带。为了能更好地理解能带图,可以用碳原子来进一步叙述。之所以用碳原子,一方面是因为它是硅等的同族元素,位于元素周期表的同一列,另一方面,电子数是同列中最小的。当碳原子之间的距离,从无限远处拉近的时候,会有如此的变化:- 离散能级1s(上面有2个电子)会演变成能价带,完全被电子占据;
- 能级2s(上面有2个电子),2p(可以有6个电子,只占了2个)之间会发生发生交叠分裂成价带(完全被电子占据)和导带(完全没有电子)到此,应该能大概理解,那个文章开头的能带图是怎么来的,为什么在T=0K的时候,半导体的价带中是被电子完全占据的,导带中没有电子。
(2) 为了能分析MOS电容,还得在材料图上添砖加瓦
虽然知晓了能带图大概是怎么来的,但是想要分析MOS电容,还需要在能带图上加上点东西。电子是费米子,所以电子的占据概率符合Fermi-Dirac分布,严谨详细的推导见文献[1]。在本征半导体中,n=p,所以其费米能级位于禁带中。当费米能级为Efi的本征半导体,进行p型掺杂后,费米能级Ef会下移;进行n型掺杂后,费敏能级Ef会上移。(3) MOS中三种材料的能带图
MOS,是metal-oxide-semiconductor,很好的反应了MOS的材料组成。虽然metal大多数情况下是导电性很强的多晶硅,但是不妨碍把它当成metal来进行分析。
在上篇中,有讲到p型半导体的费米能级是处于本征半导体费米能级Efi的下方。
因为绝缘体的能带图和本征半导体的能带图,除了禁带宽度有区别外,很类似,所以直观上,可以做一下迁移,也就是绝缘体的费米能级Ef也位于禁带中。
但是金属呢?
金属的能带图有两种,如下图所示,一种是部分填充,存在禁带;一种是价带和导带重叠。所以我理解的时候犯了难,我不知道怎么迁移了 。
。
deepseek说,在T=0K时,费米能级定义为电子占据的最高能级,我琢磨琢磨,应该可以接受。
因为在[2]中,有说,能级被电子占据的概率,符合Fermi-Dirac分布,即: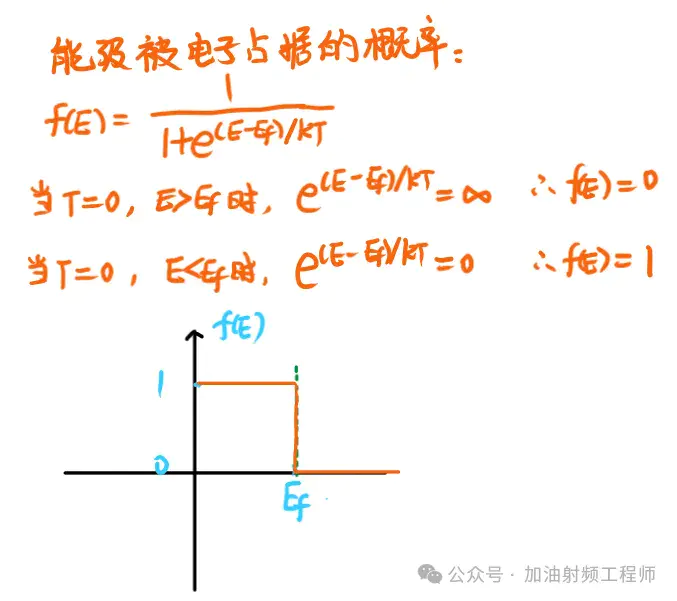
所以,当E>Ef时,能级被电子占据的概率是0,也就是说,当T=0K时,费米能级Ef是电子占据的最高能级。
又因为两种能带的金属,不管是部分填充还是价带和导带重叠,在导带中,都有电子,所以费米能级是位于导带内。
所以,MOS中三种材料的能带图,如下图所示。
但是,要分析这三种材料相互接触时,能带图的变化,还需要另外两个量。
一个是材料的电子亲和性(electron affinity),其是材料导带底与真空能级之间的能量差。在真空能级处,电子彻底放飞,从材料中脱离出来,进入真空中。电子亲和性,主要由材料本身决定,不依赖于费米能级的位置和材料的掺杂浓度。
一个是功函数,其是材料的费米能级与真空能级之间的能量差。
将这两个量,添加到MOS中三种材料的能带图,则是:
(4) 当三种材料接触后,会怎么样?
如果三种材料独立不接触的时候,各自的能带图,如下图所示。
为了让三种材料接触后,VG=0时,三者的费米能级都在同一水平线上,如下图所示,需要做2个假定[2],一个是在oxide和semiconductor里都没有净电荷,这样在没有外加电压的时候,三种材料各处的电势都为0;一个是metal的功函数等于semiconductor的功函数。
按照Ali教授视频所讲,Xm'和Xs'应该保持不变,因为这是材料本身的特性。(不过,这里有一点点疑惑,因为如果是Xs'保持不变的话,那感觉就出不来oxide-semiconductor接触面处的bending了,所以,我在想,教授是在VG=0的情况下讲的,虽然手势比划的是接触面处,其实是指oxide与偏远处的n-type semiconductor之间的能量差?暂时先忽略这一点)。
当VG>0时,金属的费米能级Ef,m往下移动,而Xm'不变,所以代表oxide的矩形的左边框开始往下移动,此时右边框保持固定(或者会稍稍下移??因为[3]中讲,当Ef,m往下移动的时候,会带着半导体与氧化物接触面处的能级也往下移,从而出现bending,暂时也先忽略这一点),如下图所示。此时,在oxide-semiconductor处,应该往哪倾斜,还未标注。
在[3]的3.1节中,Mark教授,介绍了通过电势来判定oxide-semiconductor接触面处能级的倾斜方向。
倾斜代表什么呢?
先直观上来推测一下,VG>0,则金属与oxide的接触面处产生正电荷,因为是n-type semiconductor,所以里面的多子是电子,电子会被金属侧的正电荷吸引,在n-type semiconductor和oxide接触面聚集,也就是说,在该接触面处电子浓度增加。
而半导体中的载流子浓度的公式为:
接触面处Ef与Ei之间的间距,与本征半导体(x--∞)相比,变大,所以接触面处的电子浓度变大,与上述直观推测相符合。
该工作区域,被称为accumulation。也就是说,当半导体是n-type,VG>0时,为accumulation;类似,当半导体是p-type,VG<0时,为accumulation。
在[3]的3.1节中,Mark教授,介绍了通过电势来判定oxide-semiconductor接触面处能级的倾斜方向。
倾斜代表什么呢?
先直观上来推测一下,VG<0,则金属与oxide的接触面处产生负电荷,因为是n-type semiconductor,所以里面的多子是电子,所以电子会被金属侧的负电荷排斥,从而留下不能移动的正离子,也就是说,在n-type semiconductor和oxide接触面处开始形成耗尽层。
而半导体中的载流子浓度的公式为:
接触面处Ef与Ei之间的间距接近于0,自由移动的电子和空穴都近似等于ni, 浓度小,且电子和空穴的电荷基本抵消。与上述直观推测相符合。
该工作区域,被称为depletion region。也就是说,当半导体是n-type,VG<0但又不是很小的时候,为depletion region;类似,当半导体是p-type,VG>0时,但又不是很大的时候,为depletion region。
金属的费米能级进一步向上移动,同时接触面更加弯曲。
而半导体中的载流子浓度的公式为:
所以在n-type semiconductor和oxide的接触面处,空穴的浓度要大于电子的浓度,开始呈现出p-type semiconductor的特性,也就是说,在接触面附近,半导体的类型发生了反转,称为inversion。这个时候空穴的产生,可能就没有那么直观了,这也是我当初看着razavi的模集时又来看半导体物理的原因。也就是说,对于MOS电容,这些空穴主要来源于半导体中的热激发。参考文献:
[1] Donald A. Neamen, Semiconductor Physics and Devices
[2] Ali Hajimiri, Analog