ProNas能量有限元方法在船舶中高频噪声预测的应用(附视频直播)
- 作者优秀
- 优秀教师/意见领袖/博士学历/特邀专家/独家讲师
- 平台推荐
- 主编推荐


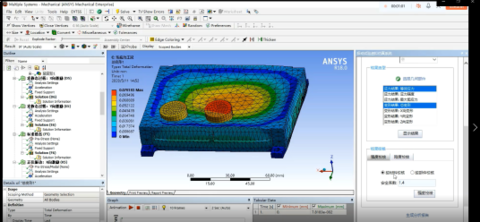
摘要:以ProNas能量有限元理论为基础,建立了船舶的ProNas能量有限元计算模型,采用大型商用正版软件ProNas对复杂激励在船舶各舱室产生的中高频结构噪声及空气噪声进行仿真计算,得到船舶各舱室声压级,并利用ProNas软件后处理功能确定激励源及传递路径处的能量分布云图,对不满足噪声目标的舱室进行了声学优化,最终解决了大型实际船舶工程的中高频噪声预测与控制问题。
关键词:ProNas能量有限元;船舶;中高频噪声; ProNas软件;声学优化
The Mid-High Frequency Noise Prediction of Ship Vessel by Applying ProNas Energy Finite Element Analysis
Abstract: Based on the ProNas energy finite element ****ysis (EFEA) theory, a ProNas EFEA ship model was established. A Large-scale commercial genuine software called ProNas was adopted to predict the mid-high frequency structure-borne and airborne noise, induced by multiple excitations in each cabin of the vessel. The sound pressure level of each cabin was calculated, The distributed energy cloud map around both excitation source area and tran**ission paths were displayed in the post-procession of ProNas, so the acoustic optimization against those cabins which failed the noise criteria could be easily applied. Finally, the mid-high frequency noise prediction and control of real large ship vessel was achieved successfully.
Key words: ProNas energy finite element(EFEA) theory; ship; mid-high frequency noise; ProNas software;acoustic optimization.
0 引言
复杂结构的中高频噪声的控制一直以来都是各工业领域研究的重点与难点问题,尤其对于大型船舶其内环境相比其它工业产品更加独特[1]:结构形式纵横交错,舱室众多,噪声诱因复杂,声源品种繁多密集,噪声强度较大,噪声频域带宽且持续稳定,结构噪声与空气噪声相互转化。以上这些特点,就使得船舶噪声控制起来更加困难。2014年7月国际海事组织(IMO)签订生效的新的《船上噪声等级规则》要求居住区部分舱室声压级在旧规范的基础上降低5dB(A),这就要求船舶工程设计人员需要采取更加有效的控制手段来降低船舶噪声。
目前预测结构噪声及空气噪声的理论体系相对完善,并已将理论应用于大量实际工程中。按激励源频率及具体工业产品,可将振动和噪声的问题划分为低频、中频及高频问题。低频结构的响应具有随机和确定性,且为全局模态,工程中常用的数值方法为有限元(FEM)、边界元(BEM)等。
理论上,有限元方法可计算任意结构的振动场,但是为了能准确反映结构的振动特性,划分单元的网格长度要求要远低于结构中弯曲波的波长。这样随着频率的增加,结构弯曲波波长变小,结构网格需要进一步细化,对计算资源要求较高,且结构模态密集,重叠交错,响应表现出不确定性,具有了统计的概念,因此,有限元和边界元就不再适合解决中高频问题。
统计能量分析(SEA)用于解决中高频问题,且模态越密集,其计算精度就越高。但统计能量分析不能保证子系统的空间变量信息的完整性[2],难以精确预示子系统内能量密度分布[3]且子系统的划分需要一定的经验,不易进行实际结构形态的设计与优化[4],模态密度及耦合因子的准确与否直接影响结果的准确度[5-6]。所以为了更好的控制中高频噪声,就需要有更好的理论方法。
能量有限元法[7](EFEA)是一种预测中高频动响应的新方法,它是以波动理论为基础,将结构离散化,在单元之间建立能量密度关系式,从而求解得到所有节点的能量密度。能量有限元法以有限单元为对象,保证了模型的完整性,但是在结构突变处引入了大量重复节点,求解效率得不到平衡,能量有限元理论目前可以解决一些简单的有限元噪声问题,对于复杂问题的应用依然比较困难。
ProNas能量有限元是在统计能量分析及能量有限元理论的基础上,以有限单元为研究对象,混合了SEA及EFEA理论,利用有限体积法及差分法推导出得类似于SEA的理论方程,联立求得每个有限单元的能量密度。ProNas能量有限元法避免了在结构突变处引入重复节点,保证了求解精度和计算效率,是一种具有较高研究价值及应用价值的中高频噪声控制方法。
本文着重介绍了ProNas能量有限元理论原理且应用ProNas商业软件对大型实际船舶的中高频噪声进行了仿真计算,求解得出船舶各舱室声压级。
1 ProNas能量有限元基本理论
ProNas能量有限元法可有效解决结构振动系统中高频噪声问题,它包含了能量有限元法(EFEA)及统计能量分析法(SEA)的优点,具有更大优势。
ProNas能量有限元方法是在波动理论上建立的一种功率流方法,通过波动形式求解结构微元体运动方程,并将波动形式下的动能密度、势能密度及功率流进行周期内时间平均和
局部空间平均,得到能量密度与功率流的关系,代入稳态下能量平衡方程中可以得到能量密度控制方程;采用一定的数值离散方法对控制方程进行离散,得到能量有限元方程;在结构存在耦合的地方考虑波的反射和折射,求出耦合处能量密度与功率流的关系;最后进行总系数矩阵的组集,得到总体的方程,从而求出能量密度。
有限体积法的基础是将模型离散成若干个控制体,而这里的控制体可理解为有限元的“单元”,这样,ProNas能量有限元就是以单元为研究对象。
弹性介质中的能量平衡方程[8]如下:
式中,e为能量密度;为结构的应力张量;为位移向量;为输入功率;为时间和空间的平均耗散功率。
稳定状态下,子系统功率平衡,可以表示为:
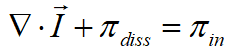
声能量密度和耗散功率之间的关系如下:

声能量密度和声强之间的关系如下:

因此,可以得到能量密度方程:
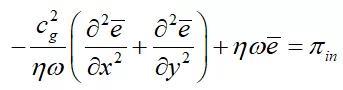
式中,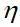 为阻尼损耗因子;
为阻尼损耗因子;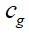 为群速度,
为群速度,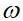 为圆频率。例如对于简单三段梁模型如图1所示。
为圆频率。例如对于简单三段梁模型如图1所示。
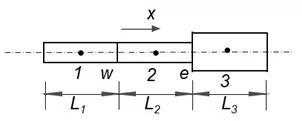
图1.简单三段梁示意图
能量有限元方程如下:
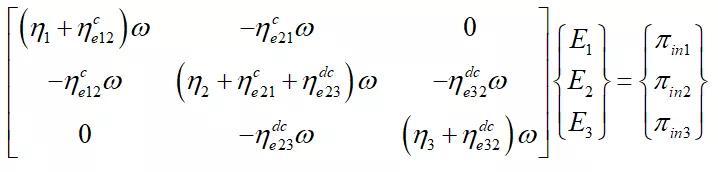
一般性地,ProNas能量有限元矩阵方程可以表述为:
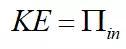
式中,K 为总体能量密度系数矩阵;E为节点能量密度向量;为总体输入功率向量,求解该式就可以得到单元的能量密度。由上式可知 ,ProNas能量有限元矩阵方程与SEA方程形式一致,为一次线性方程,易于求解。
2 船舶模型建立
2.1船舶前处理模型
本文以某客箱船为例。利用Patran前处理软件对某客箱船进行有限元建模,如图2所示,该模型共有单元114358个,节点94357个。该客箱船全长约200米,船宽约25米,采用的是双机双浆配置,主机为两台低速机。该船的前部为载货区域,后部为居住区域和机械处所。因对居住区域及机械处所噪声控制要求较高,同时为了节省计算时间,本案例截取局部模型,即仅对居住区域和机械处所进行研究。
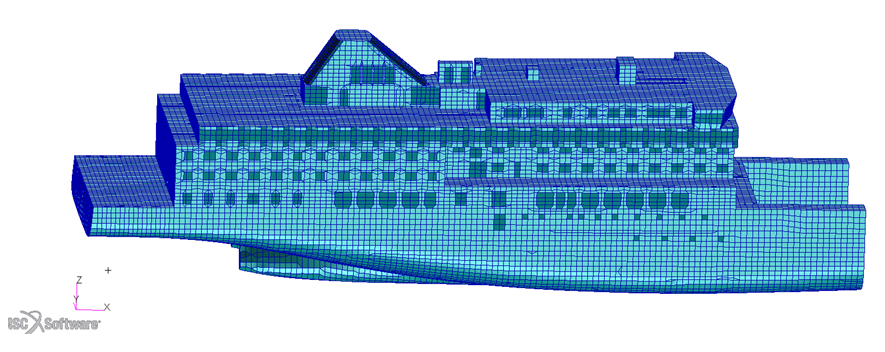
图2.某客箱船有限元模型
2.2 ProNas软件模型处理
ProNas软件是国内知名公司安世亚太联合国际最先进的中高频噪声专家资源开发的中高频噪声仿真分析软件,拥有国内自主软件著作权的自主可控的中高频软件,是能量有限元分析(EFEA)和统计能量分析(SEA)领域的代表性解决方案,代表着振动噪声工程界新一代的前沿技术。
本案例通过ProNas声学仿真软件分别对船舶的结构噪声与空气噪声进行了仿真计算。将Nastran格式模型导入ProNas软件中,如图3所示。通过ProNas软件声腔自动识别功能自动划分声腔子系统,如图4所示。软件自动耦合声腔子系统和其临近贴合的结构单元,这样能量即可在结构单元与声腔子系统之间进行交换。然后对各舱室结构单元进行声学材料设置,如甲板敷料、绝缘布置材料,设置门窗材料等,如图5所示。
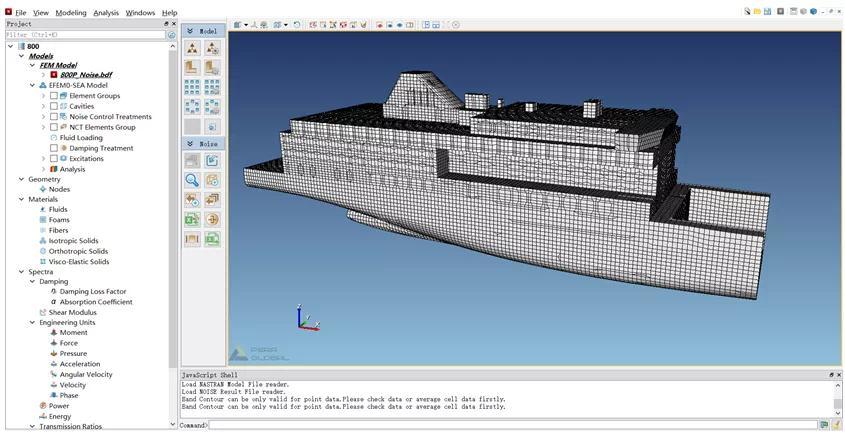
图3.某客箱船ProNas有限元模型

图4.某客箱船各舱室声腔子系统

图5.某客箱船声学材料施加
3 船舶模型激励输入
船舶噪声[9-10]主要包括主机噪声、螺旋桨噪声及水动力噪声。其中主机噪声是船舶噪声中最强的噪声源,主机噪声主要分为空气辐射噪声、排气噪声和结构噪声,空气辐射噪声有燃烧噪声和机械往复运动碰撞噪声,成因复杂,一般实测得到。螺旋桨噪声也是船舶的主要噪声源,螺旋桨直接产生的噪声有空泡噪声,空泡噪声会引起船体结构噪声。水动力噪声主要是由于高速海流的不规则起伏作用于船体湿表面,激起船体的局部振动并向周围介质(空气与水)辐射的噪声。
该客箱船模型根据实际情况所受激励载荷主要有24个,分别为主机、螺旋桨、发电机、空压机、空调、风机等。其中主机、发电机、螺旋桨与船体作用,船体会振动产生结构噪声。其它主要激励源通过空气传递到船舶舱室内,产生空气噪声。结构噪声源通过ProNas软件分别在各设备的有限单元表面以速度级及加速度级方式加载,如图6所示。空气噪声源通过ProNas软件分别在各激励源所在声腔子系统内以声功率级方式加载,如图7所示。主机速度级激励如图8所示,螺旋桨加速度级激励如图9所示。

图6.某客箱船结构噪声载荷分布图
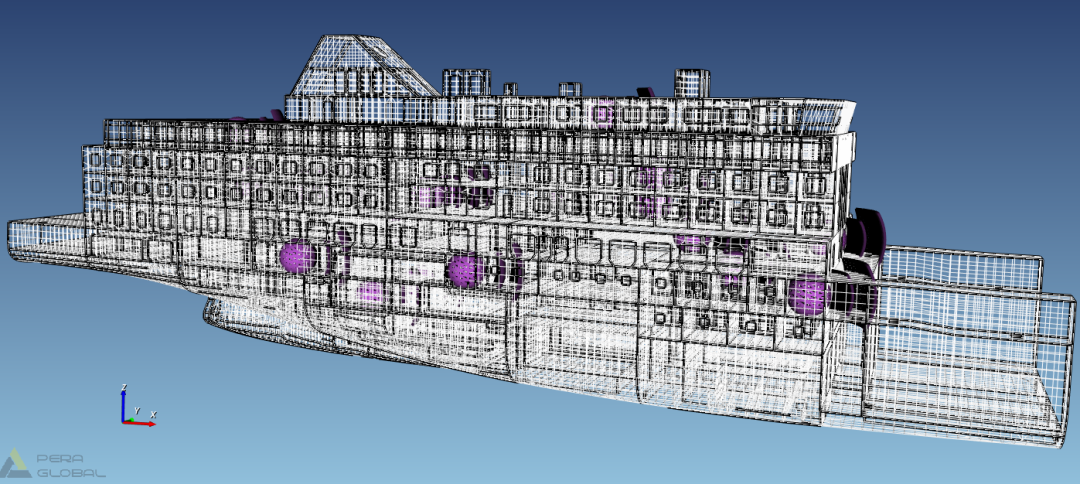
图7.某客箱船空气噪声载荷分布图

图8. 主机激励频谱图
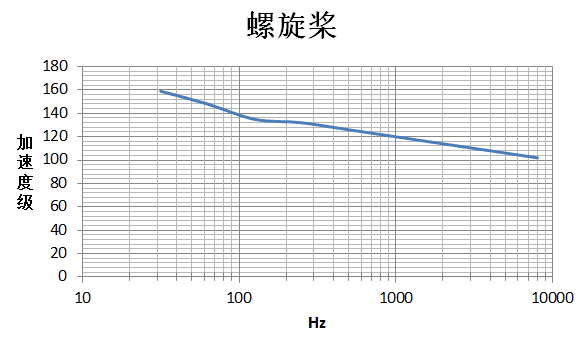
4 船舶结构噪声及空气噪声分析结果与优化
4.1船舶噪声分析结果
在倍频程中心频率63-8000Hz下分别将该客箱船结构噪声模型与空气噪声模型提交ProNas软件求解器,经过ProNas软件计算,可得到各舱室声压级水平,图10、图11分别为该客箱船在中心频率为500Hz时结构噪声仿真得到的结构速度云图与舱室声压云图,图12与图13分别为该客箱船在中心频率为500Hz时的空气噪声仿真得到的结构速度云图和舱室声压云图。

图10.结构速度云图(500Hz-结构噪声)

图11.舱室声压云图(500Hz-结构噪声)

图12.结构速度云图(500Hz-空气噪声)

图13. 舱室声压云图(500Hz-空气噪声)
该客箱船舱室声压分析结果见表1,部分舱室声压级不满足目标值。
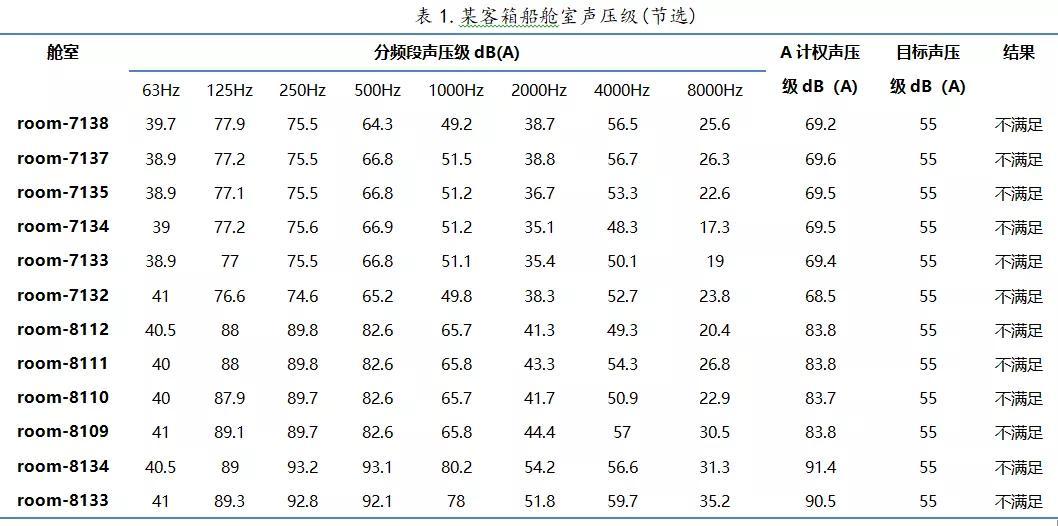
4.2优化方案
对于结构噪声超标的舱室,常见的优化方法为敷设阻尼。阻尼材料是将结构振动板的振动能量快速转化为热能,从而减弱金属板的弯曲振动,阻尼材料通过这种方式有效的控制金属板的结构辐射噪声。
通过云图分析可知,本案例结构噪声超标,多为主机与螺旋桨结构噪声引起。由于该客箱船采用低速机,主机与船体钢板直接螺接,船体底部振动区域较大,且底部钢板厚度约为25mm-30mm,在实际应用中,阻尼层厚度一般为金属板厚度2-4倍,因此如果采用常规的在激励源处阻尼敷设方法,阻尼用量相对较大,成本较高。
又由于船舶结构复杂,结构噪声和空气噪声相互转化,因此常规阻尼敷设方法对超标舱室噪声控制效果一般。针对以上特点,本案例通过ProNas软件后处理界面可直观精确显示传递路径处能量分布,即在不达标舱室处直接敷设阻尼,采用这种敷设方法,阻尼用量及成本在可控范围内,且噪声控制效果显著。图14为常规敷设阻尼方法,图15为本案例阻尼敷设方法。

图14.常规敷设阻尼区域

图15.本案例敷设阻尼区域
对于空气噪声不达标舱室,结合ProNas软件后处理结果云图,本案例采用以下优化方案:
第一、部分娱乐室及放映室等地面浮动地板均改为50mm岩棉 钢板 阻尼 钢板型,再在上侧加10mm流平甲板敷料。
第二、部分甲板厨房抽风机室的内部,艉、中、艏面增加4mm钢板做成双墙舱壁,形成密封夹层空间,两层钢壁都设阻尼涂料。
第三、甲板房间合计26间处所的天花板需穿孔(穿孔面向室内),孔径按1.8mm。壁板**孔。
第四、在部分甲板机舱棚两侧直接面向公共处所和房间的舱壁,在外侧增加4mm压筋板做成的舱壁,形成密封的夹层空间,夹层内设50mm隔音棉。
第五、部分甲板均设9mm厚阻尼涂料处理。
4.3实船仿真与测试结果对比
经过以上方案优化并多轮仿真计算,优化以后各舱室噪声控制效果较好,将以上优化方案应用到实船设计中,并对该客箱船实船舱室进行了噪声测试,如表2所示,大多舱室噪声数值满足设计要求。
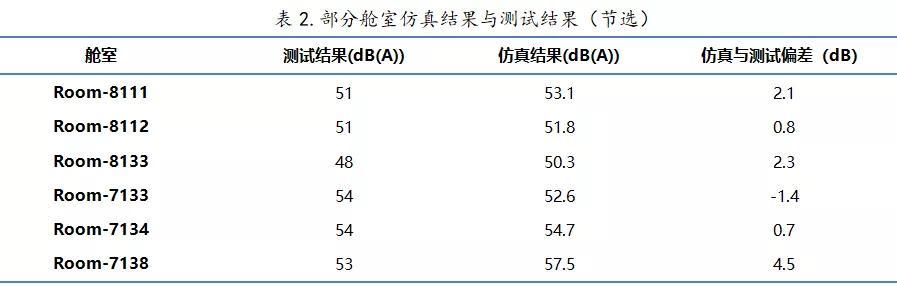
5 结论
本文简要介绍了ProNas能量有限元方法,在此基础上应用ProNas软件建立了某客箱船声学模型,进行了整船的结构噪声与空气噪声仿真计算,对结构噪声及空气噪声不达标舱室进行仿真优化,并与实船测试结果进行对比,得出了以下结论:
第一、ProNas能量有限元方法是一种用于预测和解决船舶及其它工业产品中高频噪声的可行性及有效性方法,具有很大的理论意义与现实价值。
第二、采用ProNas能量有限元方法,可避免常规中高频方法子系统建模操作的复杂性与专业性,提高仿真计算精度。
第三、ProNas能量有限元方法不需要判断子系统模态密度,不需要确定系统之间的耦合因子,既保证模型的完整性,又提高仿真的时效性。
第四、ProNas软件为解决中高频噪声提供了新的方法,为改进船舶设计参数提供了科学依据,提高了船舶的噪声设计质量,缩短研发周期,节约开发成本。
第五、ProNas软件仿真得到的船舶结果与实测结果的最大误差值的绝对值在5dB(A)内,满足模型的预测精度。
参考文献
[1] 陈小剑. 船舶噪声控制技术[M]. 上海:上海交通大学出版社,2012:12-107.
[2] 林志立. 能量有限元法的模型及其在车身中的应用[D]. 中国科学院大学博士学位论文,2018,宁波.
[3] 原凯,王建民,韩丽,等. 能量有限元在振动与噪声预示中的研究进展[J]. 强度与环境 2015. 42(3):12-19.
[4] 祝丹晖,解妙霞,孔祥杰,等.复杂机械结构中高频动响应能量有限元方法研究[J]. 中国工程科学,2013,15(1): 107-112.
[5] 庞剑,谌刚,何华. 汽车噪声与振动----理论与应用[M]. 北京:北京理工大学出版社,2005: 54-62.
[6] 陈书明,王登峰,马一功,等. 模态密度计算精度对车内噪声预测精度的影响[J]. 吉林大学学报,2010,40(2):335-340.
[7] 孙丽萍,聂武. 能量有限元法在船舶结构中的应用[J]. 哈尔滨工业大学学报,2008,40(9):1491-1494.
[8] BERNHARD R J. The family of EFA equations and their relationship to SEA[C]//Proceedings International Conference Noise and Vibration Energy Methods.Lyon:[s.n.] 2000:248-257.
[9] 翁长俭. 船体振动学[M]. 大连:大连海运学院出版社,1992
2020年12月10日20时,笔者将在仿真秀平台公开直播中高频噪声仿真前沿技术探秘《基于ProNas能量有限元混合算法——实现某大型船舶舱室 汽车整车噪声预测》,感兴趣的朋友可以关注。