Matlab 做重要性抽样(含代码
本文摘要(由AI生成):
本文介绍了过冷水在近期实用大数定理做积分运算时遇到的抽样问题。直接抽样法虽然简单,但在被积函数起伏大的情况下可能导致较大误差。为提高抽样效率,文章提出了重要抽样法,即对被积函数贡献大的区域多取样,接近零的区域少取样。此外,还介绍了随机抽样法和期望估计值法的原理和应用步骤。这些方法有助于提高积分运算的精度和效率,展示了数学在实际问题中的灵活应用。
过冷水在近期经常会实用到大数定理做积分运算。大数定理会涉及到抽样方法,平常采用的抽样都是均匀抽样,这样抽样方法有时候不太准确。有什么问题呢?请随过冷水来看。
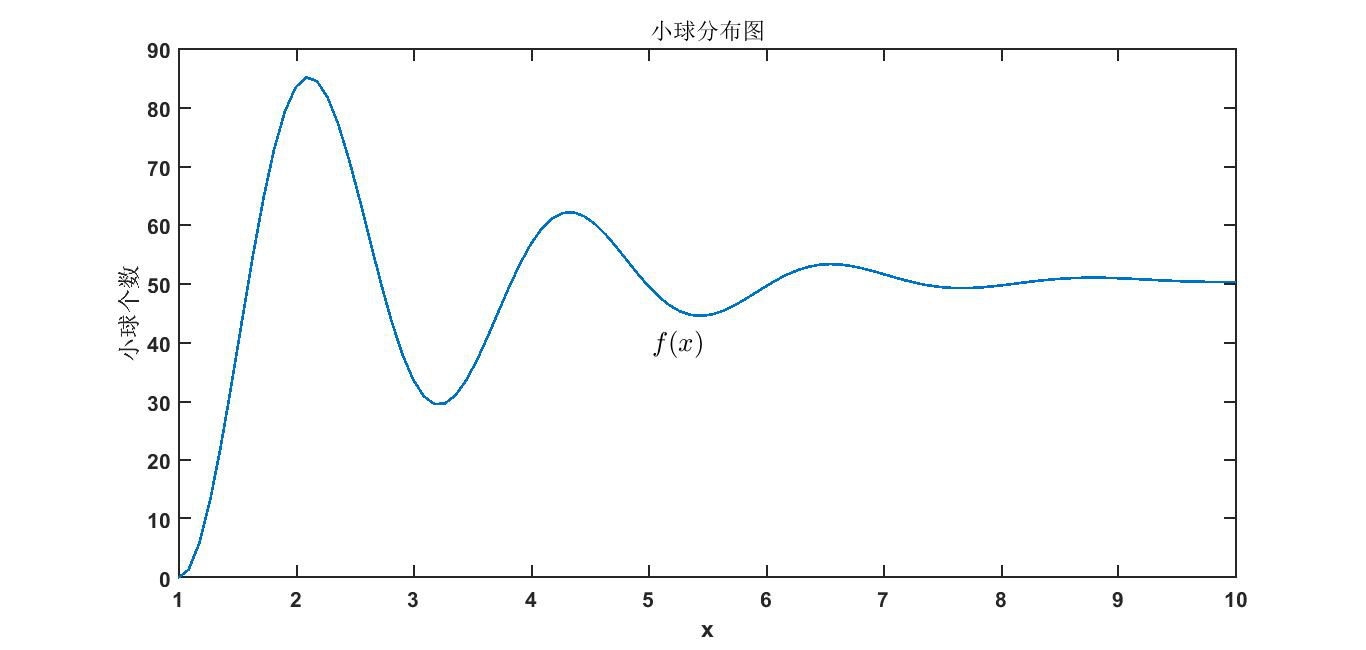
对该图像用Monte Carlo 求积分
clear all warning off feature jit off n=1000; x=1 9*rand(1,n); y=50*( 0.9664-1.22*exp(-0.1811*x.^1.5).*sin(-2.805*x 4.49)) 2.25; I=9*sum(y)/n I = 449.9730 y2=50*( 0.9664-1.22*exp(-0.1811*x.^1.5).*sin(-2.805*x 4.49)) 2.25; N=vpa(int(y2,x,1,10)) N = 451.21022742407789201299004991588
比较可知Monte Carlo在抽样只有1000次的时候有明显的误差,我们不能总归结于通过抽样次数的增加来增加计算精度,应该考虑一下其他可能性。过冷水以前关于Monte Carlo方法求定积分问题没有在随机数的抽样上下功夫,之前都是在积分域内均匀随机抽样,称为直接抽样法。直接抽样法完全不考虑被积函数的特点。所以,当被积函数f(x)在积分区域内起伏很大的话,直接抽样法在函数峰值左右取到的样本数目相对偏少,于是求积分的误差就很大,反之,如果所有抽样点的函数值都很接近,直接抽样法的精度就很高。所以对于提高抽样效率来说对于积分值贡献很大的区域抽样要多取些,被积函数值接近于0的区域可以少取些点。这就是重要抽样法,也就是要对函数的分布情况改变抽样的分布。
随机抽样法:若随机变量X的累计分布函数G(x)连续,则随机数r=G(x)在区间[0,1]内均匀分布将等式两边均被G-1(.),作用得到G-1(r)=x,连续,可见以上定理提供了连续型随机数的生成办法。
步骤1:由分布的概率密度分布函数g(x)的积分

得到累计概率分布函数。
步骤2:令G(x)=r,然后从反函数求得G-1(r)=x,该x的取值就能够符合概率密度分布函数g(x)
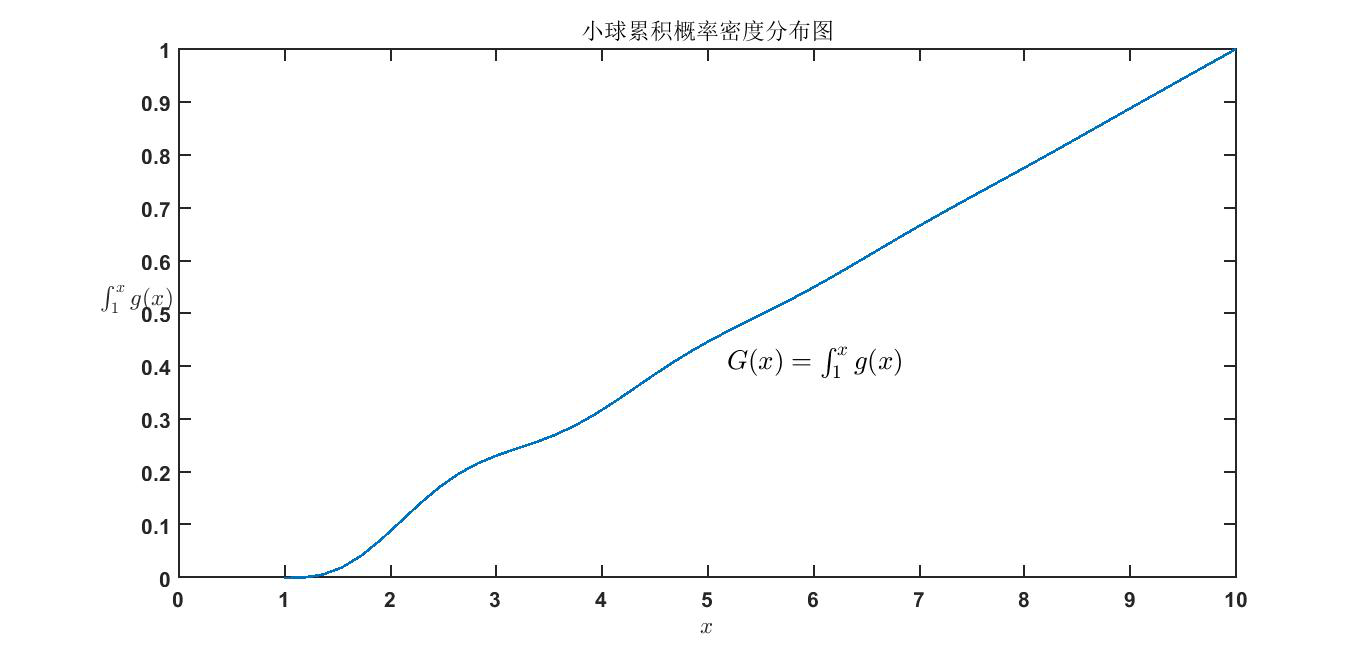
通俗的讲就是对原分布的y值进行均匀抽样,则x就是非均匀抽样。大致思路为:

x取均匀值,y为非均匀分布。
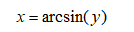
对y进行均匀抽样,这x就是非均匀抽样点。改思路就是这样简单,我们具体怎样在实际中使用呢?
假设积分函数为:
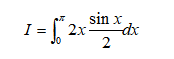
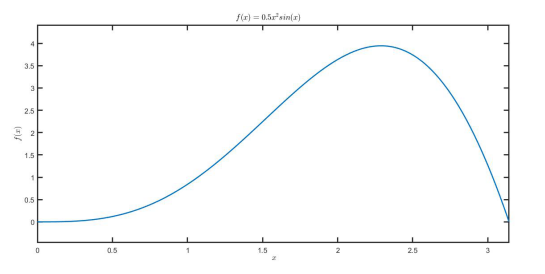
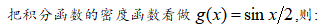
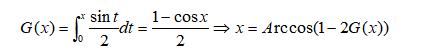
原来是对x进行均匀抽样,现在是对G(x)进行均匀抽样,反推x的抽样,代码见附件。
由程序可知当直接对x均匀抽样的结果比对sin(x)/2均匀抽样反推x的结果要好!这是因为过冷水只是为了给大家展示案例,实际选取的抽样函数并不合理,如何选取均匀抽样的函数这个要根据实际函数进行分析,在此过冷水了解的不多,就不做拿来主义了,有需要了解的读者可以查看相关资料。
期望估计值法:期望值估计法的原理就是数学中的变量替换。
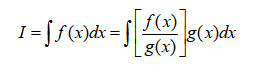
变换后的等式右边g(x)dx是一个新的分布,g(x)为分布的密度函数,原来要求对dx均匀抽样,然后对抽样点出的f(x)求值,现在我们变成了对 g(x)dx均匀抽样,对抽样点处的f(x)/g(x)求值。此时就相当于对dx不均匀抽样,即对这些不均匀分布的抽样点上的f(x)求值。
通俗的讲就是对图像上累计概率密度进行均匀抽样,然后求对应的x值,在用x进行大数定理的计算。
计算步骤为:
(1)根据分布密度函数g(x)产生随机点;
(2)求出抽样点x处的f(x)/g(x)函数值,积分
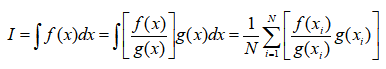
本期关于重要性抽样方法的分享就这么多。知识是逐渐积累的过程,过冷水最初只知道的用int()函数求积分,接触到用Monte Carlo求积分,然后又看到用大数定理求积分,最后抽样方法的改变对大数定理、Monte Carlo都有影响,学问做细后发现好多有趣的点,希望过冷水的抛砖引玉能够激起大家探索的兴趣。