预应力同心管柱的屈曲荷载能超过欧拉临界荷载吗?ANSYS告诉答案
一直有个疑问,就是预应力同心管柱的屈曲荷载能否提高?能否超过欧拉临界荷载?最近鼓捣了一下,答案是否定的,即预应力不能提高同心管柱的屈曲临界荷载。
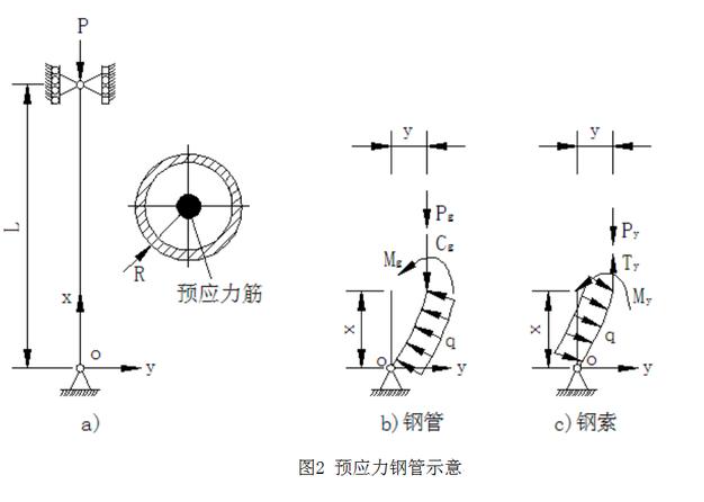
本文所指预应力同心管柱是:钢管中穿有钢索且二者中心重合,对钢索施加预应力,使钢索受拉并使钢管受压,且假定钢索与钢管密贴但可在钢管内滑动,然后锚固在钢管两端,形成预应力索和钢管同心的自平衡组合构件—简称预应力钢管。屈曲荷载指构件失稳时的极限荷载,与欧拉临界荷载意义相同。
1.理论推导及结论
欧拉临界荷载公式的推导如图1所示,材料力学中都有此推导过程。

预应力钢管的屈曲荷载推导时,取图2的隔离体。要注意的是:钢索张力和钢索致钢管压力是一对作用力和反作用力,图2中假定为竖向,若假定与轴线相切更准确,但结果相同。
截面控制方程推导过程(感谢效松教授的指导)如图3所示,推导过程中钢索和钢管同心,且钢索与钢管密贴(也可假定采取工程措施达到此假设),其余与欧拉公式推导过程相同。

推导结论:预应力同心管柱的屈曲荷载与预应力无关,与欧拉临界荷载完全一致。
2.ANSYS特征值屈曲和大变形非线性分析
为验证上述理论推导的正确性,采用如下模拟方法:
(1)钢管采用梁单元BEAM189模拟(BEAM188也可),钢索采用LINK180模拟。
(2)钢管和钢索密贴条件,也就是两个构件单元节点的横向位移相同(竖向建模),即在横向耦合自由度(本例为UX);但其余方向不能耦合自由度(如UY),也就是钢索可以在管内滑动,且不考虑二者摩擦。但钢管两端点与对应的钢索端点需完全耦合。
(3)为简单起见,只做面内分析,即约束面外的平动位移自由度(本例为UZ)。
(4)为达到张拉预应力值(ANSYS之LINK180施加预应力及生死单元应用),需先进行静力分析的试算,以保证计算完成后钢索的预应力为张拉应力,如例子中的张拉系数tcoef=1.0479312。
(5)在进行特征值屈曲分析时,因ANSYS屈曲荷载=特征值屈曲系数×所有荷载,这个所有荷载当然包括初应变或施加预应力的降温荷载,因此也要不断更改外荷载(如本例中的P0)试算几次,确定外荷载增大系数(如HZXS=12.83644),进而在特征值屈曲分析完成后,特征值屈曲系数=1,也就是ANSYS屈曲荷载=1.0×(HZXS×P0)。
(6)在非线性分析中,即所谓的非线性屈曲分析,按第一阶特征值屈曲模态施加1/10000的缺陷,即柱中位置设有0.8mm的侧向弯曲(可以用NLIST查看)。
(7)非线性分析前,必须删除原来的外荷载。因在特征值屈曲分析时,竖向荷载是特征值屈曲荷载,如果忘记删除,会造成荷载的动荡。如本例在模型更新后执行了“FDELE,ALL,ALL”命令。
(8)本例屈后仅计算了一部分,仅为验证理论。如果需要,可以接着继续计算屈后行为,不收敛时可采取相应的求解措施,此文略过。
(9)在屈前和刚过屈后求解过程中,钢管应力和钢索的应力都不大,均未达到塑性状态;随后随着位移的增大,应力会超过材料的屈服点,但本例只进行了几何非线性分析。众所周知,特征值屈曲分析不考虑任何非线性行为;非线性屈曲分析时,应考虑几何非线性和材料非线性,在本例中增加材料本构,便可得到自平衡预应力钢管的极限荷载。
图4为计算模型和荷载-位移曲线计算结果,图5为不同荷载下的变形过程。命令流如下所示。
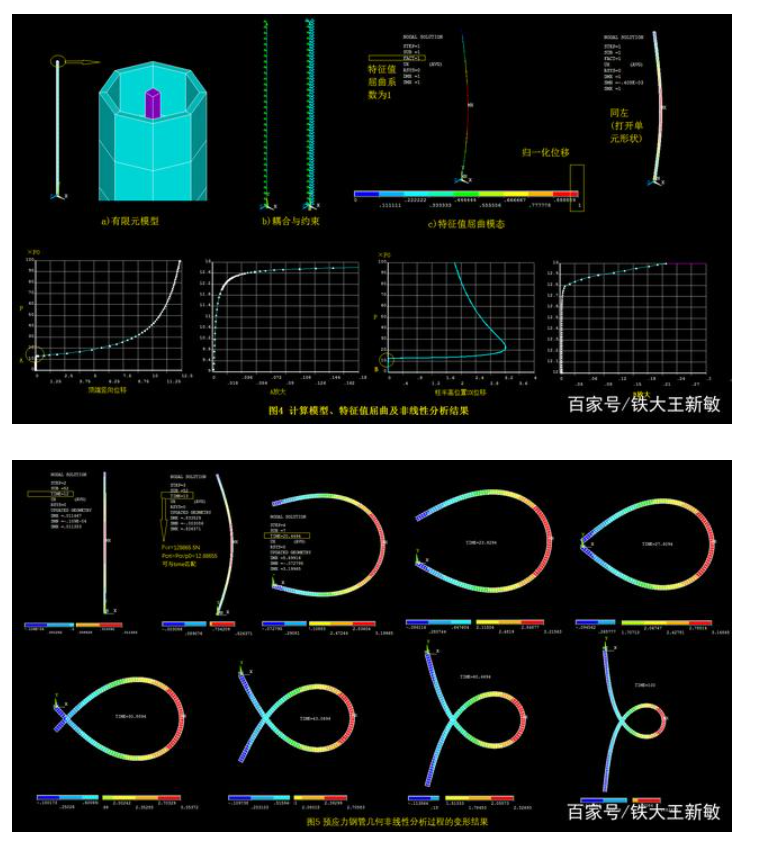
本例的欧拉临界荷载为128865.5N;预应力钢索张拉应力为800MPa,ANSYS特征值屈曲荷载为1.0×12.83644×10000=128364.4N,与欧拉临界荷载的误差不足4‰。而非线性屈曲的拐点位置在12.8~12.9之间,也非常接近欧拉临界荷载。
ANSYS的特征值屈曲分析和非线性屈曲分析也表明,预应力同心管柱的屈曲荷载与预应力无关,与欧拉临界荷载完全一致。
FINISH$/CLEAR$/FILNAME,YYLJZZ
/PREP7$H=8$RI=0.05$RO=RI 0.008
SIGY=800E6!预应力筋张拉应力
AY=140*1E-6!预应力筋面积
PI=ACOS(-1)$EMOD1=2.1E11
EMOD2=1.95E11
LPX=1E-5!线胀系数
AG=PI*(RO**2-RI**2)
IG=PI/4*(RO**4-RI**4)
PCR=PI**2*EMOD1*IG/(H*H)
GSIG=800E6*AY/AG!预应力引起的管应力
TCOEF=1.0479312!张拉系数(试算)
TT=SIGY/EMOD2/LPX*TCOEF!降温值
P0=10000!施加初始的竖向荷载
K,1$K,2,,H$K,3,1$K,4$K,5,,H$L,1,2$L,4,5
ET,1,BEAM189$ET,2,LINK180
MP,EX,1,EMOD1$MP,PRXY,1,0.3
MP,EX,2,EMOD2$MP,PRXY,2,0.31
MP,ALPX,2,LPX
SECTYPE,1,BEAM,CTUBE$SECDATA,RI,RO
SECTYPE,2,LINK$SECDATA,AY
LSEL,S,,,1$LATT,1,,1,,,3,1!柱划分
ESIZE,0.25$LMESH,ALL
N1=NODE(0,0,0)$NTOP=NODE(0,H,0)
NSEL,NONE!索划分
LSEL,S,,,2$LATT,2,,2,,,,2
ESIZE,0.25$LMESH,ALL$N2=NODE(0,0,0)
N3=NODE(0,H,0)$ALLSEL,ALL
!顶底耦合起来
CP,NEXT,UX,N1,N2$CP,NEXT,UY,N1,N2
CP,NEXT,UX,NTOP,N3$CP,NEXT,UY,NTOP,N3
!其余耦合UX
NSEL,ALL$NSEL,U,LOC,Y,0
NSEL,U,LOC,Y,H$NSEL,R,LOC,X,0
CPINTF,UX$NSEL,ALL
!约束上、下端及所有UZ
D,N1,UX,,,,,UY,ROTY
D,NTOP,UX$D,ALL,UZ
!预应力定义
ESEL,S,TYPE,,2$BFE,ALL,TEMP,,-TT
ALLSEL,ALL
!特征值屈曲分析
/SOLU$ANTYPE,0
HZXS=12.83644!荷载系数
PSTRES,ON
F,NTOP,FY,-P0*HZXS
SOLVE$FINISH
/SOLU$ANTYPE,1
BUCOPT,LANB,1$MXPAND,1,,,YES
SOLVE
!几何非线性分析
FINISH$/PREP7$ DETA=0.8/1000
!施加0.8MM的缺陷,即万分之高度缺陷
UPGEOM,DETA,1,1,YYLJZZ,RST
FDELE,ALL,ALL!删除原荷载
/SOLU$ANTYPE,0$NLGEOM,ON
OUTRES,ALL,ALL$NSUBST,10$ALLSEL,ALL
TIME,1$SOLVE!仅预应力
!外荷载
TIME,12$NSUBST,100,,50
F,NTOP,FY,-12*P0$SOLVE
TIME,13$F,NTOP,FY,-13*P0$SOLVE
TIME,100$NSUBST,200,,100
F,NTOP,FY,-100*P0$SOLVE
/POST26$NSOL,2,NTOP,U,Y
PROD,3,2,,,,,,-1$XVAR,3$PLVAR,1
NMID=NODE(0,H/2,0)
NSOL,4,NMID,U,X$XVAR,4$PLVAR,1
综上所述,预应力同心管柱的屈曲荷载与欧拉临界荷载一致,不会因为预应力而提高钢管的屈曲荷载。但有趣的是,从推导过程(也可数值模拟)可知,在预应力同心钢管装配过程时,无论预应力多大,钢管都不会失稳直到材料屈服。

---------------------------------------------------------------------------------------------
版权声明:
原创文章,来源铁大王新敏,本文已经授权,欢迎分享,如需转载请联系作者。