厚度方向仅一层实体单元所导致的计算问题及对策
1.问题的提出
如图所示,1m×1m×10m的实体悬臂杆,沿着长度方向划分为1m×1m×1m尺寸的10个方块单元,左侧面固定。
首先看静力分析,右侧施加一个1000N的横向荷载,此问题的自由端变形根据悬臂梁的理论解答应为2E-5m,采用上述网格计算时会弹出如下的警告信息,随后求解失败,在Output中能看到“**all equation solver pivot term”错误信息。

如果进行模态分析,则前6阶频率计算结果几乎均为0,如下图所示为一阶模态及前6阶频率计算结果。
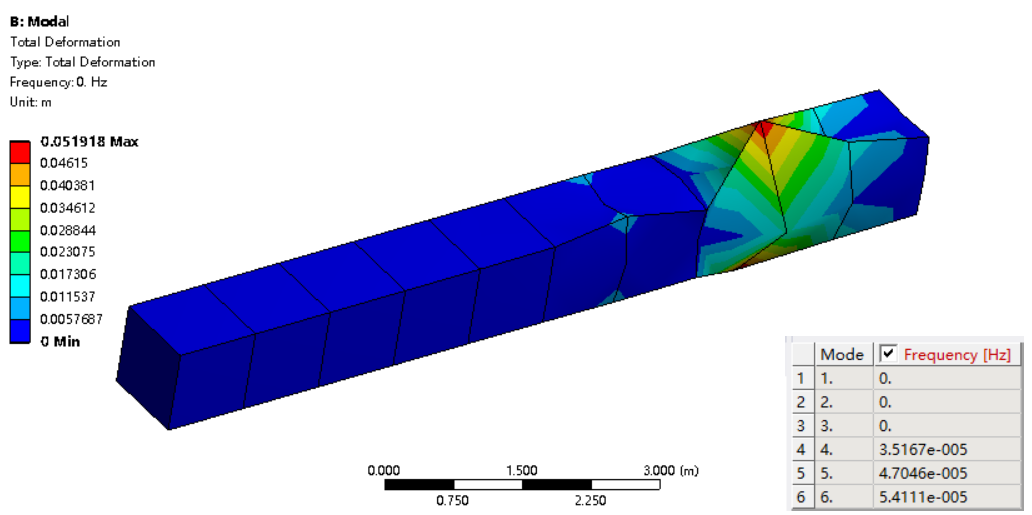
由此可见,厚度方向采用一个实体单元,即便在Workbench中默认采用了二次单元,计算也出现了由于零能模式引起的计算问题。
出现上述问题的原因,是由于采用了SOLID186单元的URI缩减积分算法,如下图所示为Output中的相关信息:

2.第一种解决方案
为了克服零能模式的影响,至少在厚度方向采用两个二次单元,得到如下图所示的网格:
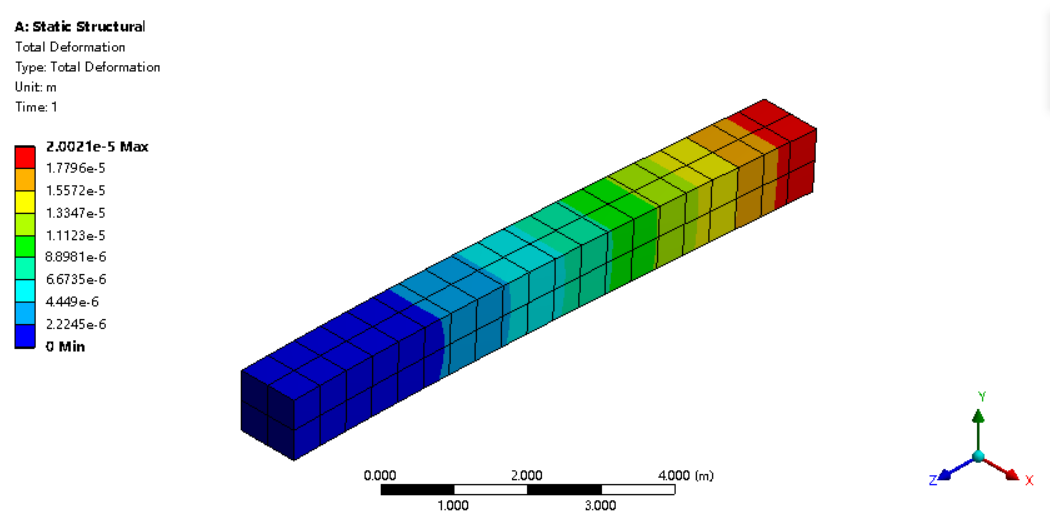
首先进行静力分析,得到梁的最大变形约为2E-5m,与理论值一致。
然后进行模态分析,得到梁的一阶振型如下图所示,一阶频率约为8Hz。
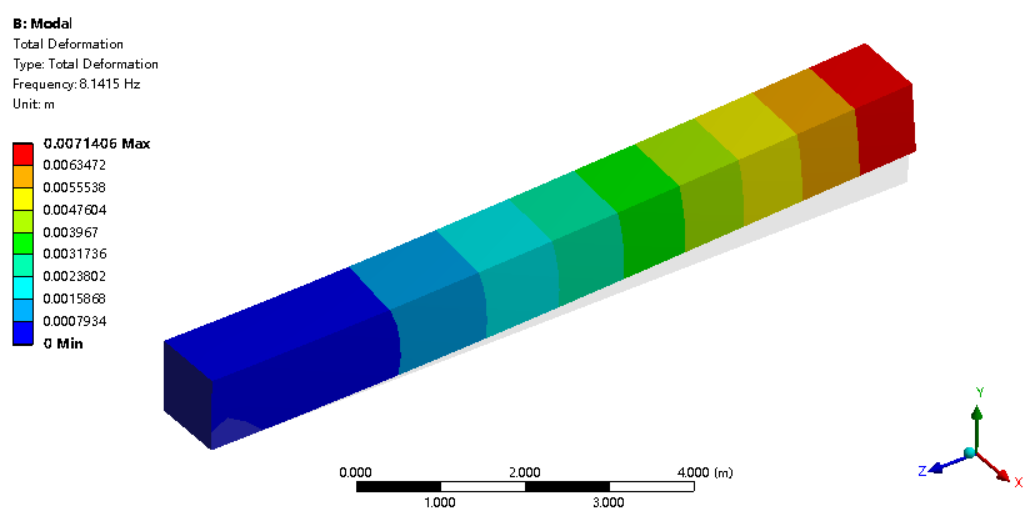
3.第二种解决方案
除了多划分一层单元外,如果仍然采用单层网格,则更换单元算法为全积分也可克服上述计算问题。
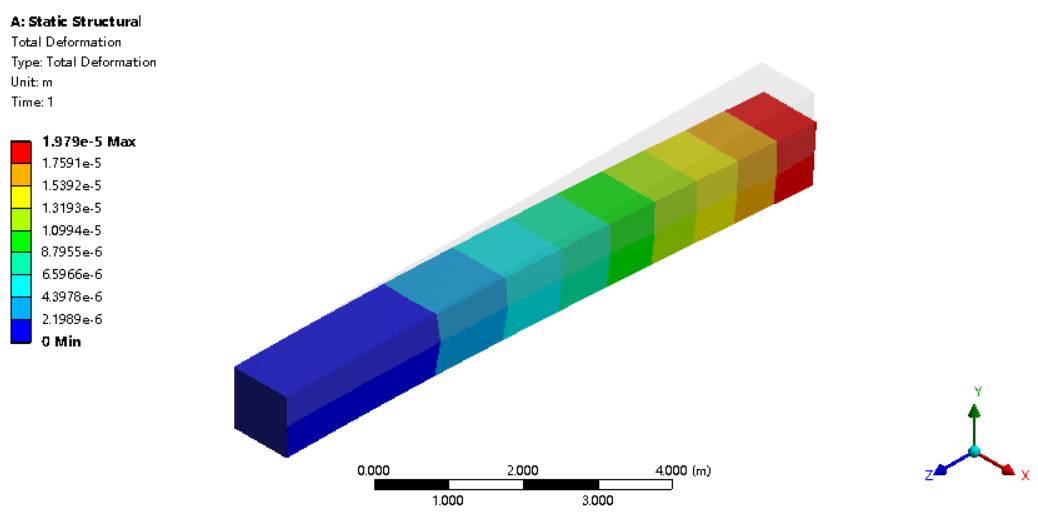
如果采用了全积分,且仍然采用单层单元,则静力计算的变形等值线如下图所示,其最大变形为1.979E-5m,与理论解答的误差很小。
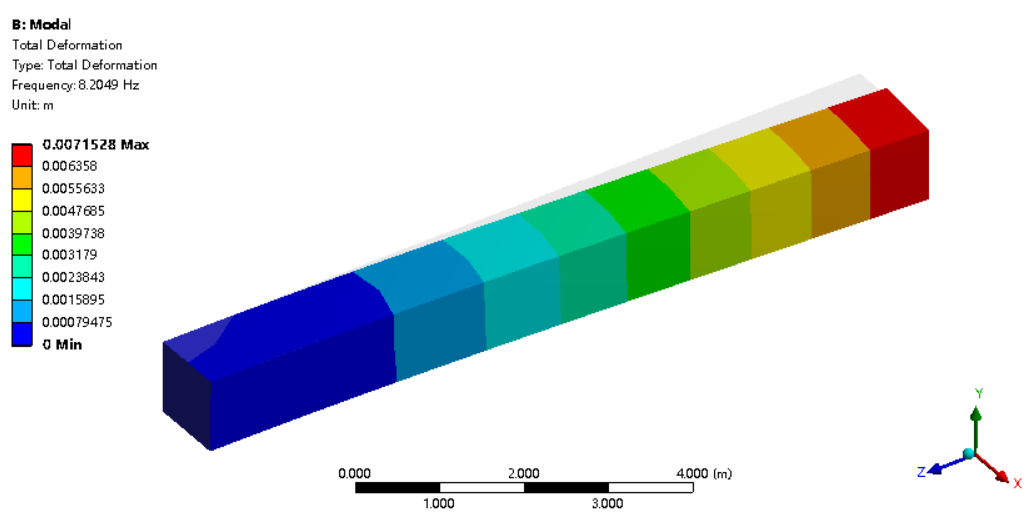
全积分单层单元计算的一阶频率也大约为8Hz,一阶振型如下图所示,计算结果正确。
综上所述,
(1)在实体结构分析中要避免厚度方向仅有一层单元的情况,否则将导致不正确的计算结果。
(2)如果在厚度方向上仅一层单元,可通过至少厚度方向两层二次单元或者单层全积分二次单元等方式获取正确解答。
登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2020-12-03
最近编辑:3年前
相关推荐
最新文章
热门文章









