力学教你变魔术:扑克牌变同张
来源:力学酒吧*****(ID;Mechanics-Bar),作者:张伟伟。
在庄老师给我教具中,有一本“神奇的魔法书”,可以在彩色、黑白、空白之间变化。庄老师录制了视频,详细介绍了魔术的表演方法和力学原理。本文是在庄老师讲解基础上,以更为常见的扑克魔术为背景整理而成,以此向庄老师在致敬!2018级范也涵同学参与了本文的视频录制和资料整理工作!
扑克牌是一种流行于全世界的纸质娱乐工具,标准扑克牌由黑桃、梅花、红桃、方块四种花色组成,尺寸为88mm*63mm。由于扑克牌的普及性,魔术师常用于制作魔术道具,本文将为大家展示一个扑克魔术,并利用力学原理揭示其中的奥秘以及其表演技巧。
力学酒吧
神奇的魔法让一副完整的扑克牌瞬间全部变成了黑桃Q,这个魔术最大的成功在于利用了人们的思维定式。一副扑克牌,共54张,大小王2张,四种花色:黑桃、梅花、红桃、方块各13张,这几乎是人尽皆知的,然而作为魔术道具,这副扑克牌是一副不正常的扑克牌。
将扑克牌展开,你会发现这副扑克牌中,黑桃Q占了整副扑克的一半,你几乎就要发现它的秘密了。

图1 黑桃Q占一半
通常情况下,扑克牌的标准尺寸为88mm*63mm,但是仔细观察,你会发现在这副牌中,黑桃Q和其它牌相比,宽度相同,但长度上略短于其它牌。我们将黑桃Q称为短牌,而将其它牌称为长牌,经测量短牌比长牌短1.5mm,比长牌少了1.7%,当然,这个长度如果不仔细观察一般很难发现。

图2 黑桃Q的长度略短于其它牌
表演时,由于长短牌的原因,从前往后拨牌,如图3(a),视频中第一种方式,正面观众看到的全部是长牌,由于长牌什么花色都有,观众看到的就像是什么一副正常的扑克。而从后往前拨牌,如图3(b),视频中第二种方式,正面观众看到的就全部是短牌(黑桃Q),这时,整副扑克牌都变成了黑桃Q。之所以会产生这样的效果,有赖于扑克牌的弹性性质,以及扑克牌与拇指、以及扑克牌之间不同的接触条件。图3中认为取扑克牌的一部分,下端以固定端替代。

图3 两种拨牌方向的不同效果
从整体来看,拇指将扑克牌压弯,扑克牌受弯后储存有弹性势能,又恢复为竖直状态的趋势,因此,在拇指与扑克牌之间形成相对运动趋势,存在摩擦力。设静摩擦系数为μ,按压力为F,可得拇指与扑克牌之间保持相对静止的最大静摩擦力为
设拇指与扑克牌之间的摩擦力为f,可写出扑克牌与拇指之间保持相对静止时的条件为f<μf(称为静止条件),而扑克牌与拇指发生相对滑动的条件为f>μF(称为滑动条件)。因此,增大按压力F,可满足静止条件;如果需要扑克牌发生滑动以备观众观察,可通过松动按压力满足滑动条件实现。满足滑动条件也可以增加拇指在水平方向的力,这相当于增加了f,当该摩擦力超过最大静摩擦力后,扑克牌也会发生相对滑动。
从局部来看,将长短牌放在一起,长牌和短牌之间,以及长短牌与拇指之间就形成了不同的接触条件,这将成为魔术的关键所在。根据拇指与扑克牌之间的关系,可将接触分为3个阶段:第一阶段,拇指与扑克牌相对静止;第二阶段,拇指与扑克牌相对滑动;第三阶段,拇指与扑克牌脱离。以下分别来考虑长牌与拇指,长牌与短牌之间在上述三个阶段的接触条件。
以图4来说明拨牌过程中接触条件的变化,及其形成的效果。由于长短牌的设置,只有长牌才能与拇指接触,画出拇指与长牌接触位置的切线,并标记法向方向n 与切向方向τ。
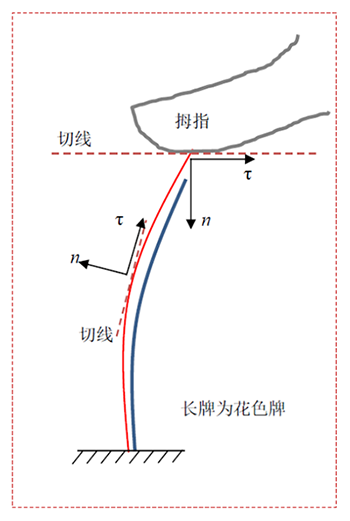
图4 接触条件分析
设接触长牌与拇指的接触面积为A,在该接触区域可传递相对于拇指面的法向力和切向力,在接触区域设拇指应力分量为σ(1),τ(1),位移分量为u(1),v(1),长牌的应力分量为σ(2),τ(2),位移分量为u(2),v(2),第一阶段相对静止时的接触条件可近似为
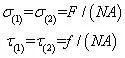

式中,N 为与拇指接触的扑克牌张数。这一阶段法向应力相等,切向应力相等,位移连续变化,这样的接触称为完全接触。更进一步可知,法向应力可近似等于按压力F 除以接触面积,切向应力可近似等于静摩擦力除以接触面积。
第二阶段扑克牌与拇指发生相对滑动,此时接触条件写为

第二阶段法向应力相等,切向应力相等,但位移发生相对滑动,因此切向位移不相等。更进一步可知,切向应力可近似等于滑动摩擦力除以接触面积。这类接触条件被称为有摩阻力的滑动接触。特别地,当摩擦系数为0,两者之间为光滑摩擦时,上式中的第2式变为

此时,被称为光滑接触。
第三阶段扑克牌与拇指分离后,扑克牌和拇指的原接触面消失,原接触面成为自由面,有

像这类变形后两弹性体脱开,则原接触面成了自由面的接触,称为脱离接触。完全接触、有摩阻力的滑动接触、光滑接触以及脱离接触,就是典型的四种接触模式。利用它们的条件也可以分析长牌与短牌之间的接触。
如图4中,选择长短牌上任一点,并标记法向方向n 与切向方向τ。设短牌的应力分量、位移分量分别为σ(3)、τ(3)、u(3)、v(3),写出三个阶段的接触条件。
第一阶段,拇指压弯扑克牌后静止,则长牌和短牌之间也静止,但由于牌面比较光滑,忽略切向力,该阶段长短牌之间的接触条件可写为下式,该阶段可认为长短之间为光滑接触。

第二阶段,当扑克牌与拇指发生相对滑动时,长短牌的曲率也会发生略微的改变,此时两牌面时间会发生相对运动,但从接触类型上来看,仍属于光滑接触,接触条件仍为接触条件(上式)。
第三阶段,当长牌与拇指脱离后,长牌将在弹性势能下由弯曲状态转变为竖直状态。此时短牌由于失去了与长牌的接触,也将在弹性势能下由弯曲状态转变为竖直状态。但在此过程中,如果长牌的恢复变形加速度大,长牌与短牌将完全脱离,法向力也为0;但如果短牌恢复变形的加速度大,则短牌“推”着长牌恢复,两者之间并非完全脱离,仍有法向接触力。
我们再回到图4中,将长短牌视为两个悬臂梁,该模型可视为在悬臂梁自由端施加集中力,则自由端挠度的表达式为

把梁视为刚度为K 的弹簧系统,则系统的等效刚度为

根据牌的长度可知,长牌的刚度小,短牌的刚度大,这将意味着短牌恢复比长牌快。在第三阶段,短牌是推着长牌恢复变形的,长牌和短牌之间在脱离阶段有正压力,但会随着变形的恢复而迅速变小。
扑克牌在恢复变形中,短牌与长牌之间存在正压力,就可以保证观众在第三阶段不会看到短牌与长牌分开,这是保证魔术**帮的重要力学条件。
除了扑克牌,根据不同的接触条件,还可以设计出其他的魔术道具,“神奇的魔法书”也是利用了这一原理。
知道了接触条件的原理,相信你也可以设计出不同的魔术道具。今年,由浙江大学王永、金肖玲、庄表中老师共同编著的《玩具和魔术中的力学》已收录在大众力学丛书中即将出版,敬请各位老师、同学关注!




