Comsol 求解热传导方程
图|(除特殊标注外)由软件截图提供
1、热传导方程
在热传导过程中,单位时间里通过某一界面传导的热量与垂直于该界面方向上的温度变化率以及界面的面积成正比,而热量传递的方向即温度降低的方向,可表示为:
 其中,λ为物质的导热系数,单位为W/(m*K);t表示温度,单位℃;q表示热流密度,单位W/m。
其中,λ为物质的导热系数,单位为W/(m*K);t表示温度,单位℃;q表示热流密度,单位W/m。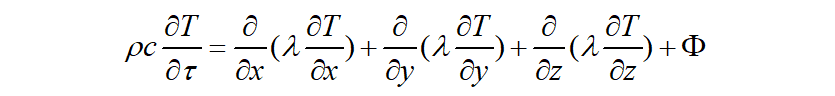
其中,ρ代表物体密度,单位为kg/m^3;c为比热容,单位为J/(kg*K);为热源在单位时间、单位体积中产生的热量,单位J;τ为时间,单位为s。
热传导方程在许多现象的数学模型中出现,而且常在金融数学中作为期权的模型出现。著名的布莱克-斯科尔斯模型中的差分方程可以转成热方程,并从此导出较简单的解。许多简单期权的延伸模型没有解析解,因此必须以数值方法计算模型给出的定价。

图1. 热传导现象
2、几何建模
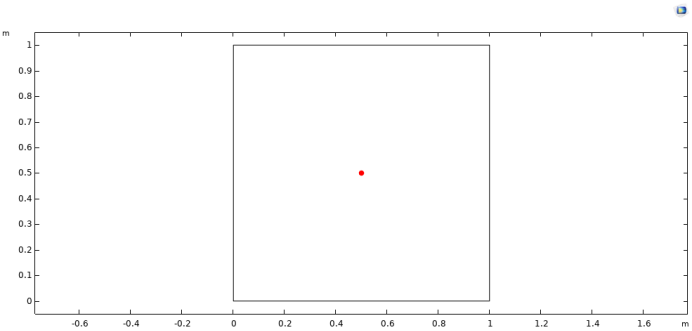
构建的1m*1m正方形几何模型如图2所示。计算过程所需参数如图3所示。
 图2. 几何模型
图2. 几何模型
 图3. 计算参数
图3. 计算参数
3、物理场边界条件
(2)u初始值设置20℃;
(3)左右边界设置狄利克雷边界条件,r取20℃;
(4)上下边界设置通量/源边界,q0取15。
 图4. 物理场边界条件
图4. 物理场边界条件
4、网格划分
 图5. 计算网格
图5. 计算网格
5、结果展示
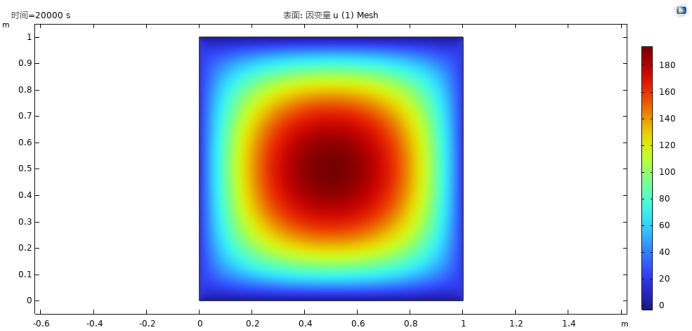
 图6. 温度分布
图6. 温度分布
 图7. 温度一阶导数分布
图7. 温度一阶导数分布
 图8. 温度二阶导数分布
图8. 温度二阶导数分布
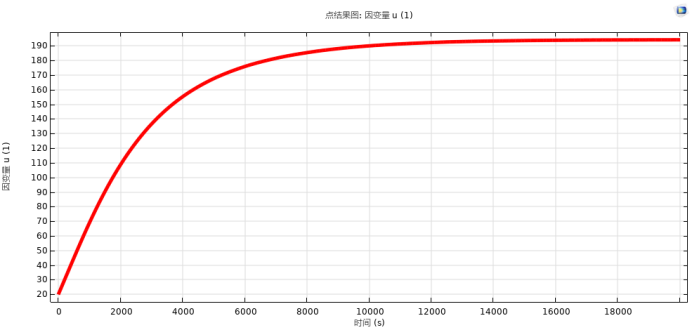
·图9. 中心点温度分布
登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2025-02-08
最近编辑:1月前
相关推荐