MATLAB空间曲面的实现方法

3月前浏览10193

本文摘要（由AI生成）：

本文介绍了使用MATLAB进行三维曲面图绘制和SIMULINK仿真中三维网格图生成的案例。首先，通过给定参数构建拟合曲面公式，并应用surf函数绘制了曲面图像和采样点。其次，通过自定义的Griewank函数生成了三维曲面图。最后，在SIMULINK中根据参数生成了三维网格图，通过改变变量值并分析曲线的变化。所有案例均涉及了MATLAB编程和SIMULINK仿真的应用。

分析数据的时候，有时需要用到三维曲面进行后处理展示，介绍了在MATLAB中生成三维曲面的几种方法：

case1

通过仿真得到x,y,z的数值，其中z(x,y)解析解难以得到的情况，即x,y,z均为数据的情况：

x=[0.05 0.1 0.15 0.2 0.25 0.05 0.1 0.15 0.2 0.25 0.05 0.1 0.15 0.2 0.25 0.05 0.1 0.15 0.2 0.25 0.05 0.1 0.15 0.2 0.25];
y=[1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 4 4 4 4 4 5 5 5 5 5];
z=[7.3 57.25 190 448 860 13 104 345 810 1550 19 150 500 1170 2250 24.6 195 650 1540 2950 30.5 242 810 1900 3580];
%cftool(x,y,z);
plot3(x,y,z/1000,'k.','MarkerSize',8)
hold on[X,Y] = meshgrid(0.05:0.001:0.25,1:0.05:5);
        p00 =      -49.15 ;
       p10 =        1685 ;
       p01 =       13.55 ;
       p20 = -2.036e 04 ;
       p11 =      -242.7 ;
       p02 =      -2.653 ;
       p30 =   1.128e 05 ;
       p21 =        1863 ;
       p12 =       24.15 ;
       p03 =      0.1044 ;
       p40 = -1.751e 05 ;
       p31 =   3.872e 04 ;
       p22 =        70.8 ;
       p13 =      -4.157 ;
       p04 =     0.03852 ;
Z=p00 p10*X p01*Y p20*X.^2 p11*X.*Y p02*Y.^2 p30*X.^3 p21*Y.*X.^2 p12*X.*Y.^2 p03*Y.^3 p40*X.^4 p31*Y.*X.^3 p22*(X.^2).*Y.^2 p13*X.*Y.^3 p04*Y.^4;
a=surf(X,Y,Z/1000);
shading interp
colormap('jet')
grid on
alpha(a,0.6)[X1,Y1] = meshgrid(0.05:0.001:0.25,1:0.05:5);
Z1=0.5 X1*0 Y1*0;
b=surf(X1,Y1,Z1);
shading interp
alpha(b,0.1)axis([0.05,0.25,1,5]);
set(gca,'FontSize',10,'Fontname', 'Times New Roman');
xlabel('\fontname{宋体}\fontsize{11}旋筒半径\fontname{Times New Roman}\fontsize{11}/m');
ylabel('\fontname{宋体}\fontsize{11}旋筒质量\fontname{Times New Roman}\fontsize{11}/kg');
zlabel('\fontname{宋体}\fontsize{11}旋筒最佳控制力矩\fontname{Times New Roman}\fontsize{11}/(N·m)');

应用：cftool

根据左框中的参数，得到拟合曲面的近似公式，然后应用surf函数将上述图像和采样点显示出来。

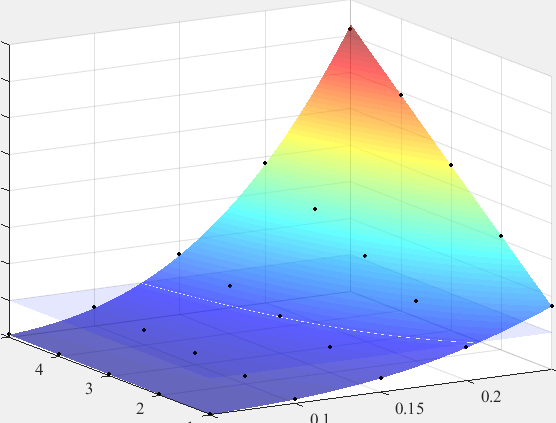
case2

z(x,y)函数可以得到：

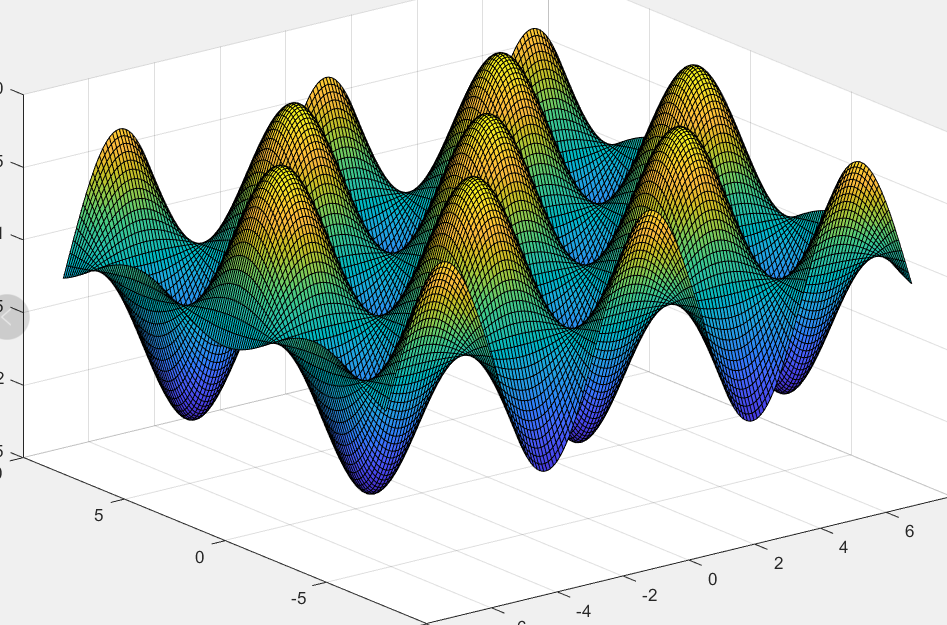
首先：构造z函数，并存为m函数

function y=Griewank(x)
% Griewan 函数
% 输入 x，给出相应的 y 值，在 x = ( 0 , 0 ,…, 0 )处有全局极小点 0
[row,col] = size(x);
if row > 1
error( ' 输入的参数错误 ' );
end
y1 = 1 / 4000 * sum(x.^2 );
y2 = 1 ;
for h = 1 :col
y2 = y2 * cos(x(h) / sqrt(h));
end
y = y1 - y2 1 ;
y =- y;
end

然后生成[X,Y]网格映射区间：

x = [-8 : 0.1 : 8 ];
y = x;
[X,Y] = meshgrid(x,y);
[row,col] = size(X);
for l = 1 :col
for h = 1 :row
z(h,l) = Griewank([X(h,l),Y(h,l)]);
end
end
surf(X,Y,z);
view([-15.5 30]);
shading interp

end

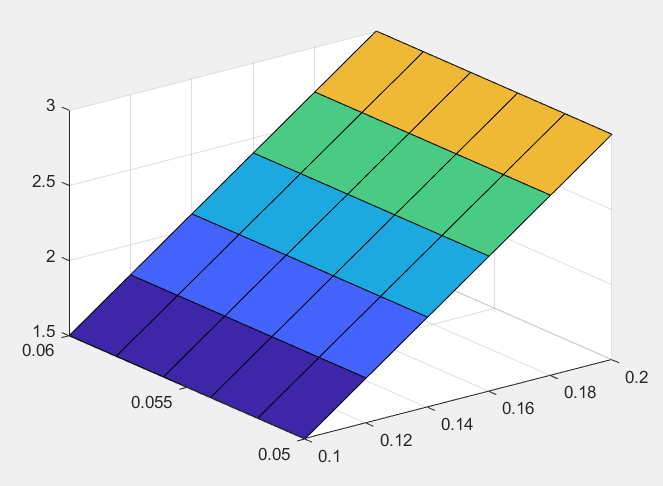
case3 SIMULINK中根据参数生成三维网格图

案例代码：

注意：

F_n、M、u_sl、u_st均是SIMULINK仿真中的变量，改变u_sl、u_st的值分析曲线。

需要将所需数据导出工作空间

F_n=15;

M=F_n/9.81;
u_sl=[0.1:0.02:0.2];
u_st=[0.05:0.002:0.06];
[X,Y]= meshgrid(u_sl,u_st);
[row,col] = size(X);
for l = 1 :col
for h = 1 :row
    u_sl = X(h,l);
    u_st = Y(h,l);
% sim函数
    sim('sim_stafl')
% z函数改这里
    z(h,l)=max(simout.Data);
end
end
surf(X,Y,z);