开尔文的 “哥伦布蛋” 问题
来源:刘延柱科学网博客,作者:刘延柱。
英国力学大师开尔文爵士 (Lord Kelvin) 于1877年提出过一个问题:“为何熟鸡蛋能在平面上直立旋转,而生鸡蛋不能呢?”。这个有趣的 “开尔文问题” 曾吸引了包括格林希尔 (Greenhill,A.G.,1880), 儒可夫斯基 (Zhukovsky,N.E.,1885), 庞加莱 (Poincaré,H.,1910), 契塔耶夫 (Chetayev,N.G.,1957), 鲁缅采夫 (Rumyantsev,V.V., 1965) 等大力学家的关注。自1880年至今已提出过多种理论解释,上世纪80年代也曾引起我国学术界的兴趣和争论。详细情况可参阅附录文章的参考文献。
开尔文问题涉及的鸡蛋能直立旋转的现象也称作 “哥伦布蛋” (Columbus egg),这个名称来源于一个有名的故事。1492年哥伦布发现了美洲新大陆。有些人不服气,说任何人乘船航行都能到达大洋彼岸。哥伦布拿了几个熟鸡蛋,请大家将鸡蛋竖立在桌上,没人能试成功。哥伦布将蛋壳的一端敲了个小洞就站住了。众人说这太容易了。哥伦布说,既然容易为何你们不去做呢(图1)。

图1 哥伦布竖鸡蛋
一个煮熟的鸡蛋可以看成是一个具有旋转椭球形状的刚体。将鸡蛋的尖端放在桌面上,如果表面绝对光滑,就只有一个几何点与桌面接触,鸡蛋的重力只要能准确通过接触点就能实现平衡。但这很难实现,即使实现,平衡也是不稳定的。稍有倾斜,重力就会朝倾斜方向推动使鸡蛋倾倒。哥伦布将鸡蛋尖端的蛋壳敲碎后,形成的小洞边缘与桌面接触。即使倾斜,只要重力不越出小洞边缘包围的区域鸡蛋仍能直立不倒。实际的鸡蛋壳表面并不光滑,粗糙的尖端存在许多突起的小点与桌面接触,这些接触点围成一个很小的区域,鸡蛋的重力只要不越出这个小区域就能直立不倒。因此,只要有足够的耐心,多试几次,即使不敲洞也能将鸡蛋竖立起来。
将一个熟鸡蛋平放在桌面上,让它快速旋转,它会突然跃起绕尖头直立旋转。于是,鸡蛋就以旋转的运动状态实现了哥伦布的要求。谈到哥伦布蛋还应提起特斯拉 (Tesla,N.) 这个人。这位塞尔维亚裔的美籍发明家、物理学家和电气机械工程师,曾有过数千件重大发明。磁感应强度的国际单位就以他命名,建在上海的以他命名的超级工厂正大量生产纯电动汽车。1893年,他在芝加哥世博会上展示了一个铁制的哥伦布蛋,以宣传他发明的交流电机。他将这个铁蛋放在环形线圈内,通以30至40赫兹的交变电流,以产生旋转磁场激起铁蛋内的感应涡流和驱动力矩,使它在托盘内绕对称轴旋转。端部与托盘接触的摩擦力能使其直立不倒(图2)。2010年,这个铁制“哥伦布蛋”也曾在上海世博会的塞尔维亚馆里亮过相。

图2 特斯拉的哥伦布蛋
与熟鸡蛋不同,生鸡蛋的情况就要复杂多了,因为生鸡蛋是一个薄壁壳体内包含液状物质的复杂物体。如果将鸡蛋的壳体视为刚体,壳内的物质近似视为液体,这个由刚体和液体组成的系统,其运动规律涉及一个动力学分支,即所谓 “充液系统的动力学”(图3)。在力学学科里,刚体是有限自由度的 “离散系统”,而液体是无限自由度的 “连续介质”。这两种不同的力学模型各自有不同的表述方式和分析方法,组合在一起讨论必然困难不少。鉴于离散系统的运动稳定性问题,已有比较完善的分析方法。因此,如能将刚体腔内的液体用离散化的模型近似地代替,就能将刚体和液体组成的复杂系统转换成一个统一的离散系统。它的稳定性问题也就迎刃而解了。

图3 平面上旋转的充液刚体
液体是不可压缩的流体。流体力学将流体区分为理想流体和粘性流体,前者忽略流体内部的粘性阻尼,而后者必须考虑。理想流体又区分为有旋流体和无旋流体,前者内部的流体团有旋转运动,而后者不存在。
如果腔内充满的液体是无旋的理想流体,Zhukovsky 证明,可以用一个等效的刚体替代腔内的流体分析其运动。刚体的质量分布是影响其运动的重要因素,刚体动力学里用惯性张量作为刚体质量分布的数学描述,由刚体相对各个坐标轴的惯性矩和惯性积组成。具有规则几何形状的充液腔所对应等效刚体的惯性张量都有现成公式可查,对动力学研究已不构成困难。
但我们要分析的对象是旋转中的充液刚体,不允许忽略腔内液体旋转的可能性。因此,必须将液体视为有旋流体,不可能采用 Zhukovsky 的等效刚体模型。除非腔体为理想球形,只有这种特殊情况,允许将腔内流体凝固成球形刚体在腔内转动而不受腔壁的约束,从而离散化为3个转动自由度的离散系统。但鸡蛋并非球形,这种简化方法也不能套用。
在流体力学中,有旋流体内各个质点处流体团的旋转状态是利用速度场的旋度来描述。旋度也称为涡量,是流体场的空间和时间的函数。可以证明,椭球形腔体内的流体虽不能像刚体一样转动,但允许做一种特殊的流动,其每个质点有完全相同的旋度,这种特殊流动可称之为 “均匀涡旋运动”。因此,对于椭球腔的特殊情形,可将旋度作为流体的离散变量。球腔作为椭球腔的特例,腔内流体的旋度就转化为球形刚体的角速度了。鸡蛋很接近椭球形,应该能适用这种离散化方法。在流体力学里,理想流体的旋度必须满足亥姆霍兹 (Helmholtz,H.) 方程的限制。于是,利用刚性壳体的角速度矢量ω 和腔内液体的旋度矢量Ω 导出充液刚体的动力学方程,与亥姆霍兹方程联立,就能利用离散系统的稳定性分析方法对鸡蛋的直立旋转稳定性作出判断。
利用上述近似的力学模型进行分析,设a 和c 为椭球的赤道半轴和极半轴,λ=c/a 为椭球的半轴比,α 作为表示液体在系统中所占成分的参数,α =0或1分别 对应于不充液或液体占全部体积的两种极端情形。再引入参数δ=mga/Aω0² ,经过必要的数学推导,可导出受扰运动为周期运动的条件:
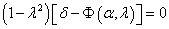
其中,函数Φ(α, λ) 定义为

此条件可用于划分渐进稳定与不稳定之间的分界线。在 (λ,δ) 参数平面内对不同α 作出的稳定域边界曲线如图4所示,其中图(a)和图(b)分别为α=0和α=1情形,如蛋壳的质量予以忽略,可分别作为熟鸡蛋和生鸡蛋的简化模型。鸡蛋的半轴比λ 约为 1.4,以λ<1表示鸡蛋的横躺状态,λ>1为直立状态。利用静止状态,即转速为零,δ →∞时,横卧的鸡蛋稳定而直立的鸡蛋不稳定的常识,推断各个区域的稳定性。
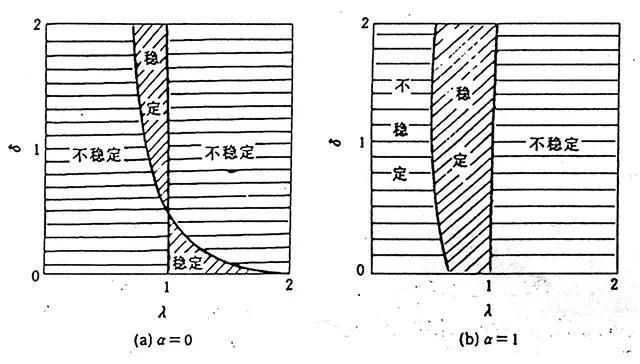
图4 (λ,δ,α) 参数空间内的稳定域
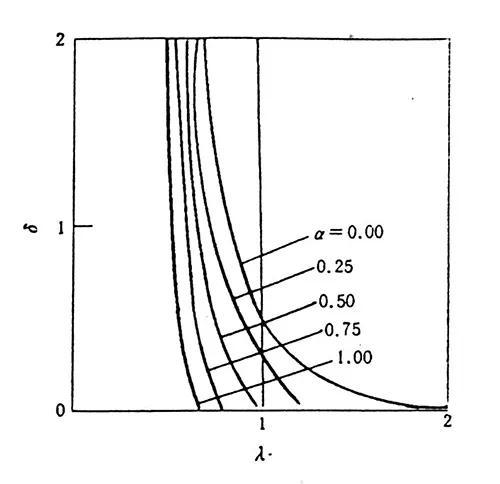
图5 参数α 变化过程中稳定域边界的演变
观察图4可看出,图(a) 显示的稳定性状态与Magnus 对旋转刚体稳定性的分析结果一致,即横躺时低转速稳定,高转速不稳定;直立时低转速不稳定,高转速稳定,此结论可用于解释熟鸡蛋的直立旋转现象。图(b) 右侧的不稳定区表明生鸡蛋直立旋转不可能稳定,左侧的稳定区表示仅横躺旋转可能稳定。在图5中,以曲线族表示α 从零增大到1的过程中稳定域边界的演变。设想将生鸡蛋加热,其液体部分从外部逐渐向内凝固,随着α 的减小,参数平面右侧的不稳定区内逐渐生长出稳定域且不断扩大的过程,开尔文问题可由此得到明确的理论解释。对数学推导部分有兴趣的读者,可参阅附录文章。
参考文献:
[1] 刘延柱. 陀螺力学(第2版),北京:科学出版社,2009,(第11章和第12章)
(原文注:本文综合自原文:刘延柱. 关于Kelvin问题. 力学与实践, 1994, 16 (3) : 43-45;刘延柱. 立春时节话竖蛋. 力学与实践,2013,35(1): 97-98 )
附录:
《 关于Kelvin问题》原文载于:力学与实践,1994,16(3):43-45




