Abaqus CEL技术(1) - 简介
1. 简介
在 Abaqus/Explicit 中提供了三种网格和底层材料之间的三种关系:
拉格朗日 (Lagrangian)

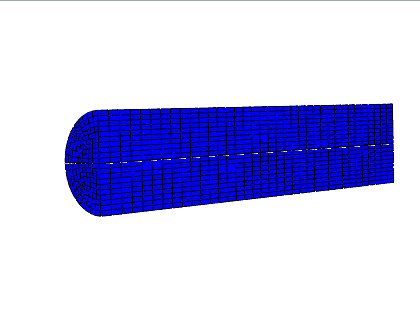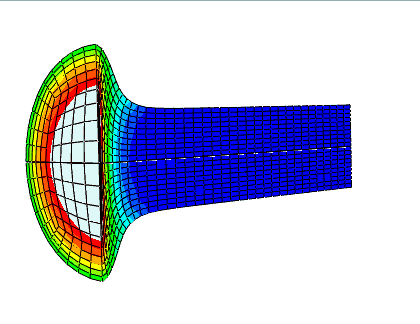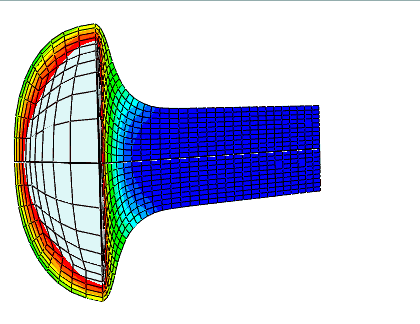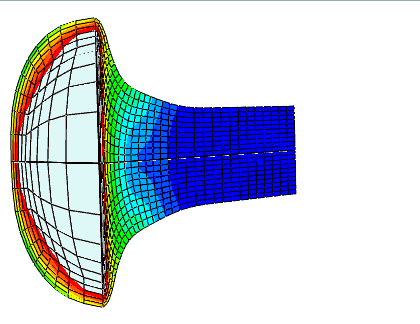
任意拉格朗日 - 欧拉 (ALE) 自适应网格

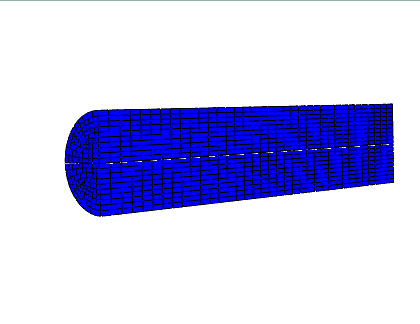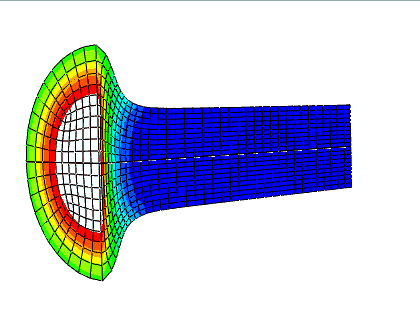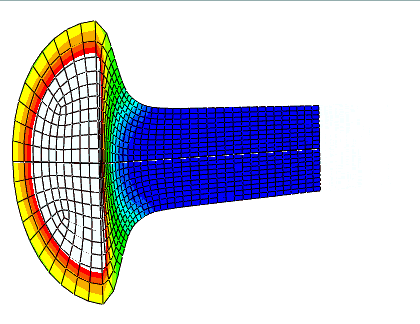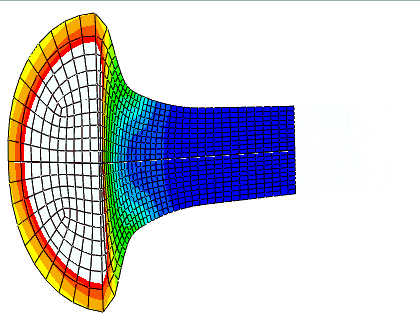
欧拉 (Eulerian)

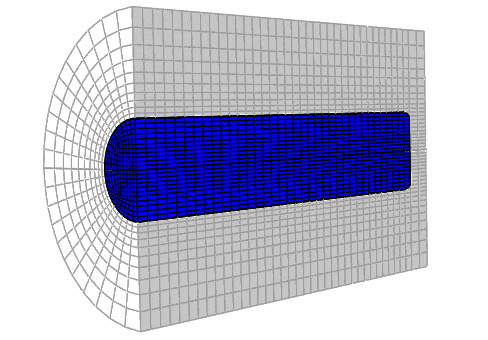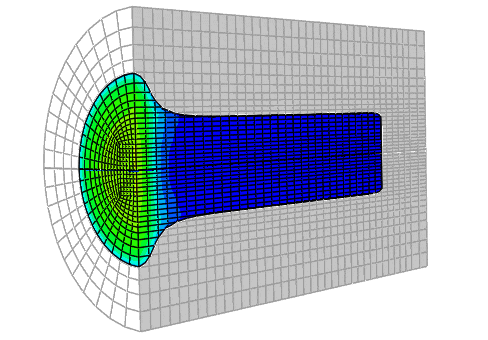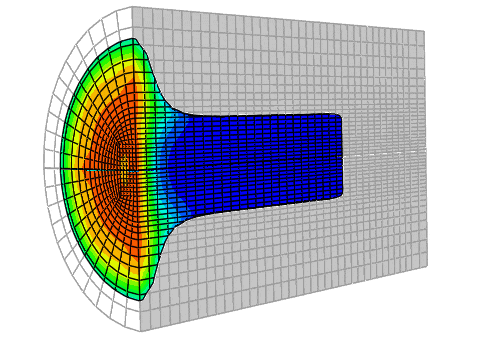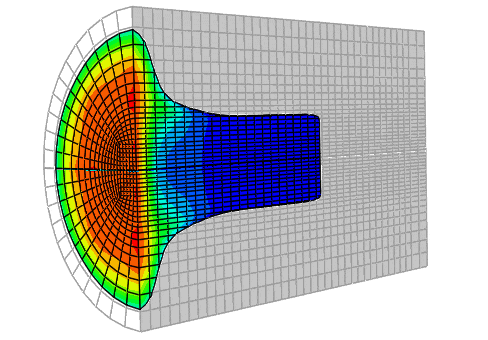
2. CEL技术
3. CEL 技术典型应用
3.1 油箱晃动

3.2 爆破荷载
研究爆炸条件下结构的结构完整性。

3.3 鸟撞机翼
对飞机安全的一种常见威胁,并造成了一系列致命事故。

3.4 锻造
锻造工艺(轧制、镦粗、压制等):通过施加压力使金属成形,金属将经历非常大的变形。

登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2024-11-03
最近编辑:3月前
作者推荐
¥399
5.0
还没有评论
相关推荐
最新文章
热门文章





