2019起重机械检验师全国F卷综合题深度解析

本文摘要（由AI生成）：

文章分析了起重机相关考试题目中的计算过程和常识性错误。首先，指出题目中关于最大弯矩的计算、静态刚性测试和悬臂静态刚度要求等方面的答案选择，并提出这些题目可能存在的问题，包括双梁起重机载荷减半的考虑、弹性模量的常识性错误（实际为E=2.1×105N/mm2而非题目中的E=2.1×106N/mm2）以及截面惯性矩的错误（题目中的I缩小了10倍）。作者通过对比实际主梁图纸和题目中的数据，发现出题者可能通过错误提高弹性模量和缩小截面惯性矩来抵消误差，使得最终答案合理。最后，作者呼吁特种设备行业前辈对文章观点进行指正。

综合题

一台通用门式起重机（MG50/10-26A2），该起重机随机技术资料显示：主要受力结构件均为薄壁箱型，全悬臂长11m，有效悬臂长7.5m,小车自重为18t,用吊钩作业，整机采用变频无级调速控制，主梁跨中和悬臂的最大截面惯性矩I=2.5x10⁹mm⁴，材质为Q235，弹性模量E=2.1×10⁶N/mm²,取g=9.8m/s^2,，请回答50-53

50，主梁在垂直面内最大弯矩可能发生在_____位置。

A,主梁跨正中   B,主梁跨度四分之一处  C,主梁悬臂侧支腿附近     D,A和C

51，主梁跨中在垂直平面内的最大弯矩值（ ）KN.m

A,2165.8     B,2210.0   C,4331.6    D,4420

52,主梁跨中静态刚性的设计计算值（ ）mm( )规范的要求值

A,47.4，符合  B,46.5，符合 C,47.4不符合  D,46.5，不符合

53，相关法规对主梁有效悬臂的静态刚性要求不大于（ ）mm

A,31.4         B,30.0       C,21.4      D,19.3

答案解析：

50，题中信息：起重机跨度S=26m，悬臂长度L=7.5m。

弯矩可能发生在主梁跨中和主梁悬臂侧支腿，需要进行比较。

跨中的弯矩：M1=FS/4=6.5F

悬臂的弯矩：M2=FL=7.5F

所以：M1<M2 

故最大弯矩在主梁悬臂侧支腿，答案选择C.

51,题中信息：起重机跨度S=26m，最大起重量50t（主钩）,小车自重为18t

最大弯矩：

M1=FS/4=(50+18)×9.8×26/4=4331.6kN▪m

答案选择C.

52，起重机的工作级别A2，跨度S=26m，最大截面惯性矩I=2.5x10⁹mm⁴，弹性模量E=2.1×10⁶N/mm²

f=FS³/(48EI)

=(50+18)×1000×9.8

  ×26000³/(48×2.1×10⁶×2.5×10⁹)

=46.5mm

起重机的静态刚性测主梁跨中静扰度

≤S/700（A2～A3）

≤S/800（A4～A6）

≤S/1000（A7）

低于定位精度要求的起重机，或具有无极调速控制特性的起重机；采用低起升速度和低加速度能达到可接受定位精度的起重机：≤S/500；

起重机的工作级别A2，同时又是无级调速，按照低标准核算

S/500=26000/500=52.0mm

由于46.5mm＜52.0mm

故符合规范要求，答案选择B

53，起重机悬臂长度L=7.5m

悬臂的静态刚度要求：

L/350=7500/350=21.4mm

答案选择C

上面解析是本人按照出题者的思路，做出来的答案，但本人觉得这道题有问题，分为以下几点进行深度分析：

1、通用门式起重机，是双梁，那么涉及到的载荷都要减半，跨中的弯矩：M1=FS/8=3.25F,不影响50题的答案；51题的答案变成2165.8kN▪m，答案变成A；52题为：f=FS³/(2×48EI)=23.2mm，这样就没有可选择的答案了。53题答案不变。

      通过52题列出的答案，似乎明白出题人的本意，这道题没当做双梁去计算，一切数据针对的是单梁起重机。所以这道题不严谨，要么答案有问题，要么题有问题。

2、常识性错误，我们都知道，钢材的弹性模量E=2.1×10⁵N/mm²（而不是试卷中的E=2.1×10⁶N/mm²），无论是Q235还是Q345，或是40Cr高强钢，弹性模量基本是相同的，所以如果结构刚性不足时，采用高强钢是无法使刚性得到加强。

     弹性模量是钢材重要的性能参数，从宏观角度来说，弹性模量是衡量物体抵抗弹性变形能力大小的尺度，从微观角度来说，则是原子、离子或分子之间键合强度的反映。金属材料的弹性模量是一个对组织不敏感的力学性能指标，所以一般工程应用中都把弹性模量作为常数。 但这道题，明显把钢材的弹性模量提高了10倍，犯了常识性错误。也许出题者是为资深人员，因为九十年代以前弹性模量常用kgf表示，E=2.1×10⁶kgf/cm²

     本人参加2017年起重机检验师考试，当时翻开试卷，也看到这个常识性错误，也就是说，至少从17年到现在，起重机检验师全国考试中，这个常识性错误一直在出现，没有得到更正。

3、弹性模量是常数，但出题者错误的提高了10倍，但最终答案却是合理，那么肯定有别的地方也出错了，两个错误叠加，最后又把坑填平了。这个错误就是截面惯性矩。

      截面惯性矩，是反映主梁抗弯性能的一个量，是截面惯性矩指截面各微元面积与各微元至截面上某一指定轴线距离二次方乘积的积分，那么我们就计算一下起重机主梁的截面参数。本人有一套50t-25.5的主梁图纸。

50t-25.5m起重机主梁图纸

      主梁截面尺寸如下图

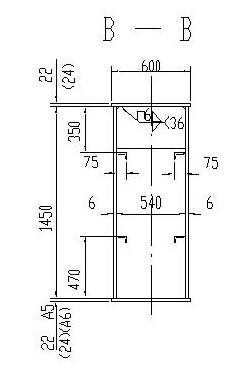
50t-25.5m起重机主梁截面

      保守计算，仅考虑上下盖板和腹板：截面宽度600mm，高度1450mm，上下盖板厚22mm，腹板厚6mm。

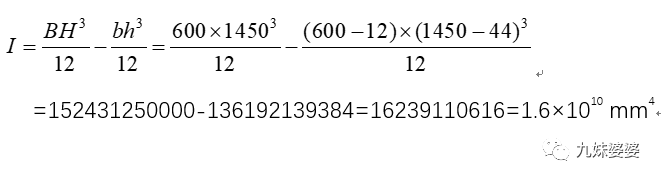
     由于没有考虑拉筋，大隔板和小筋板，因此实际的截面惯性矩还要再大一点，可知50t起重机主梁的惯性矩应该是：I=2.5×10¹⁰ mm⁴

     所以，题中的起重机主梁惯性矩，出题者错误的缩小了10倍（试卷中的I=2.5×10⁹mm⁴），正是由于出题者把弹性模量错误的提高了10倍，惯性矩缩小了10倍，错误的挖个坑，后来又用另一个常识性错误把坑填平，所以得出的最终结果却是合理的。

      起重机检验师考试，是全国性的考试，至少从我17年接触开始，这样的常识性错误就经常出现在考试试卷中，这么大的弹性模量的钢材，这个世界上就不存在。

       本文观点有不足之处，欢迎特种设备行业前辈，对本文发表的观点给与指正.