基于部分浸润效应的欧拉壁膜流动形态演变模拟仿真
■ 飞溅(splash):液滴的一部分留在壁膜中,另一部分以一些更小尺寸的小液滴离开壁面。
薄膜假设:壁膜厚度远小于壁面的曲率半径,壁膜在厚度上的属性是一致的,且壁膜流动平行于壁面。
基于以上假设下的壁膜模型分为基于场的欧拉壁膜模型和基于粒子的拉格朗日壁膜模型。本文采用欧拉壁膜模型。
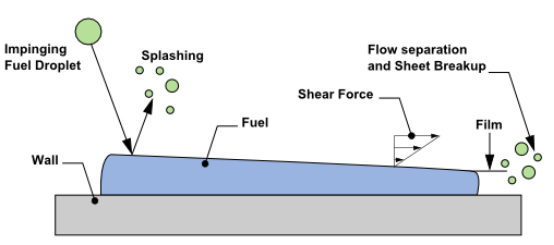
图1. 壁膜模型示意图

图2. 液滴与壁面相互作用决策图
质量守恒
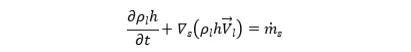
等式左边:非稳态项和对流项;
等式右边:单位面积下的质量源项,如液滴收集、壁膜分离、壁膜脱落、相变等行为下,需更新壁膜质量源项。
动量守恒

等式左边:非稳态项和对流项
等式右边:
→ 第一项:扩散项:其中,压力=气流压力 垂直于壁膜的重力分量 表面张力
→ 第二项:重力源项:平行于壁膜的重力分量
→ 第三&四项:净粘性切应力源项:气流-壁膜之间&壁面与壁膜之间
→ 第五项:动量源项:液滴的收集与分离
→ 第六项:表面力源项:壁膜的表面张力、壁膜与壁面间的接触角
能量守恒
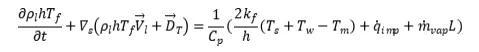
等式左边:非稳态项和对流项
等式右边:
→ 第一项:气流-壁膜间与壁膜-壁面间的净热通量
→ 第二项: :液体从气流中撞击到壁面的能量源项
→ 第三项:相变能量源项:是蒸发/冷凝的质量变化率, 是相变潜热值
控制方程的应用与求解
■ 质量守恒和动量守恒:欧拉壁膜模型的核心基础
■ 能量守恒:涉及壁膜的传热需要启用
■ 由于欧拉壁膜模型适用的液膜很薄,故采用润滑近似(平行流动),因此这些控制方程是在平行于壁面的局部当地坐标中求解的。
切应力驱动-速度线性变化
由气液交界面处外部气体流动侧,切应力与壁膜侧切应力平衡,得出外部流动产生的切应力驱动壁膜速度:

图3. 切应力驱动下壁膜速度变化
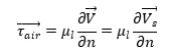

重力驱动-速度抛物线变化
由于重力与壁面切应力的平衡,壁膜速度呈现抛物线变化,壁膜速度在气液交界面的梯度为0,得出重力驱动壁膜速度:
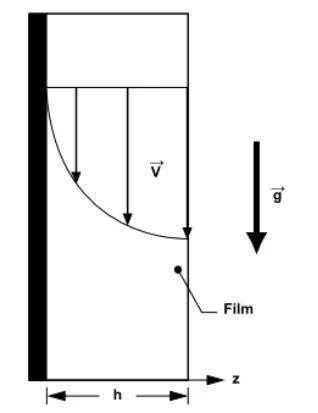
图4. 重力驱动驱动下壁膜速度变化

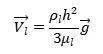
不同应用场合下的壁膜速度
■ 在有外部流体流动的重力场下,如湿空气在冷壁面的冷凝结露问题中,壁膜速度同时受气液界面的切应力与壁膜重力驱动。
■ 在无外部流体流动的重力场下,如壁膜生长流动问题中,壁膜速度完全受重力驱动。
■ 在有外部流动的无重力场下,如航天器燃料储液箱问题中,壁膜速度完全受气液界面切应力驱动。
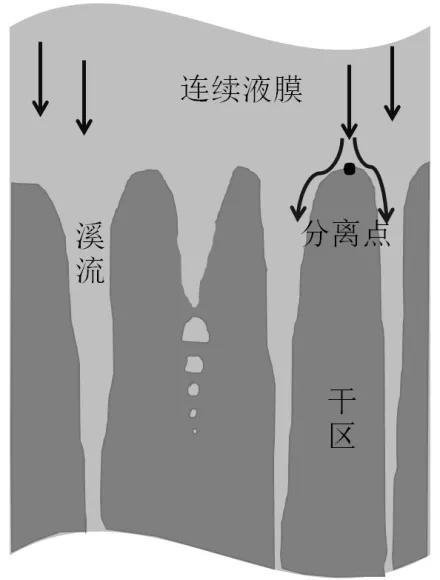
图5. 壁膜流动形态演变示意图
干区和湿润区是由壁面和壁膜的接触线划分的。
■ 壁膜湿润面积分数方程:
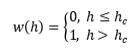
h:壁膜厚度
hc:临界壁膜厚度(fluent中1.e-7 mm)
■ 部分浸润效应形成机理:液膜与壁面间接触线的表面力限制壁膜扩散流动
■ 表面力的影响因素:壁膜表面张力σ 、壁膜流体/壁面的接触角 θw
■ 表面力方程:
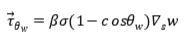
σ:表面张力
β:表征实验与模型的差异的经验系数,范围:0-10
w:壁膜湿润面积分数
θw:接触角
测试内容
建立壁膜流动模型,研究在重力场中不同流量下,壁膜的流动形态。
测试目的
探讨部分浸润效应下壁膜流动的内在机理,分析欧拉壁膜模型与部分浸润效应的条件设置思路,通过对比工况,研究不同输入参数(接触角、质量流量)对壁膜流态模拟结果的影响
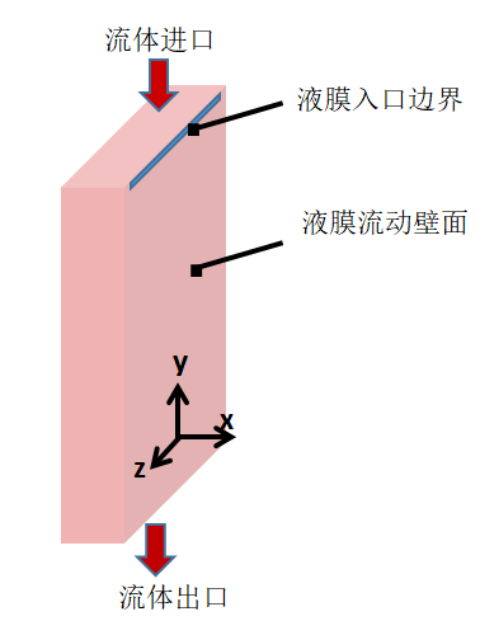
图6. 壁膜流动模型
测试流程
网格设置
采用六面体网格,网格尺寸为2x2x2mm,其中壁膜壁面中第一层网格设置为壁膜入口边界(2x80mm),其余部分设为壁膜流动壁面。
物理模型
激活能量方程、层流模型、欧拉壁膜模型。其中:
■ 欧拉壁膜模型的模型与材料设置中,需激活求解壁膜动量选项,并在动量选项中打开重力选项与压力梯度选项,在此基础上才能打开扩展项和表面张力项;在壁膜材料中选取水作为工质,设置其表面张力为0.07194。
■ 欧拉壁膜模型的时间离散与空间离散选项中,为提高计算精度,壁膜的时间、连续与动量离散均选择二阶离散。壁膜最大厚度与壁面第一层网格高度相关,设为2mm。
■ 打开质量与动量方程耦合求解和弯曲平滑,默认情况下,先计算壁膜的质量方程,再计算壁膜的动量方程。而当壁膜特征量——壁膜高度与速度是耦合时(如波浪表面的自由下落壁膜),需采用同时计算质量与动量方程的耦合求解。耦合求解主要应用于弯曲壁膜和壁膜表面张力计算的场合。

图7. 壁膜流动模型网格

图8. 欧拉壁膜模型子模型与材料设置
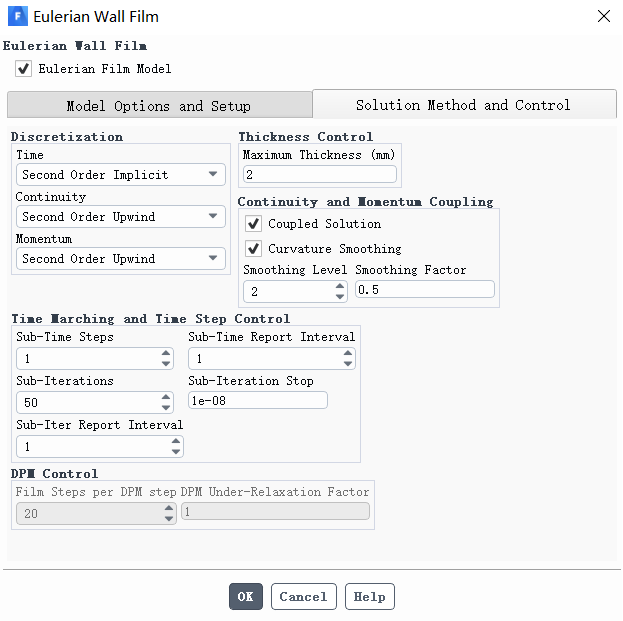
图9. 欧拉壁膜模型时间离散与空间离散选项
壁膜壁面条件设置
■ 壁膜边界入口设置
在壁膜壁面上方处设置长宽为2x80mm区域为壁膜入口边界条件,给定壁膜质量通量。对比工况设置质量通量分别为5、10、20、50、100、200kg/(m2·s),对比研究不同流量下,壁膜流动形态演变规律。
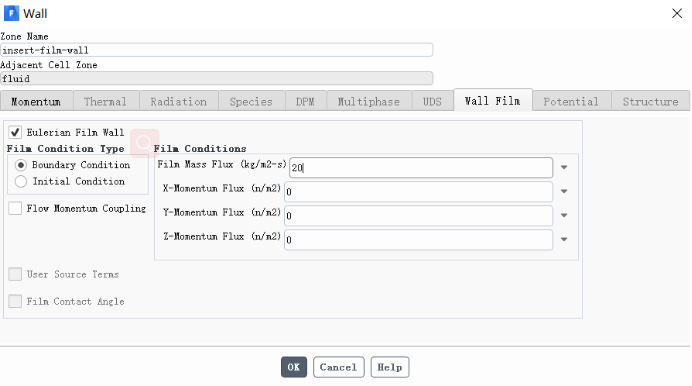
图10. 欧拉壁膜模型壁膜边界入口
■ 壁膜流动壁面设置
将壁膜壁面除壁膜入口边界外区域设为壁膜流动壁面。
壁膜部分浸润效应的条件设置:激活初始条件下壁膜接触角选项,设置壁膜与壁面间的平均接触角(对比工况分别设置为75°和15°,分别表征疏水与亲水表面)、相对标准误差(人为设定为13.5%)与表征实验与模型差异的经验系数(人为设定为1)。
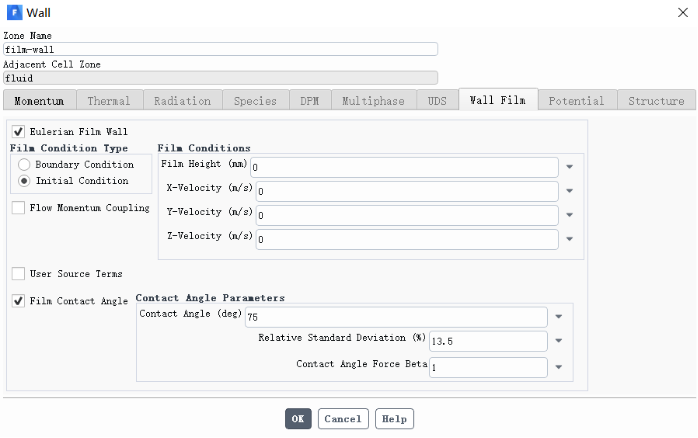
图11. 欧拉壁膜模型壁膜流动壁面
测试结果
不同质量通量下壁膜的形态演变
■ 给定壁膜/壁面接触角为75°下,质量通量为5kg/(m2·s)时,壁膜的表面张力占优,壁膜倾向于分离收缩,壁膜由上方入口受重力驱动沿着壁面往下流动,在流动初始便出现壁膜分离,形成溪流现象;
■ 随着质量通量的增加,当质量通量为10kg/(m2·s),壁膜厚度与速度明显增加,流动规律仍然呈现初始壁膜分离并形成溪流现象,但在流动下半段开始出现溪流合并现象
■ 当质量通量增加为20kg/(m2·s)时,壁膜流动现象变得更为复杂,随着时间的推移,连续壁膜的分离点明显下移,并且溪流流动过程中出现溪流合并再分离的复杂流动现象;
■ 当质量通量增加为50kg/(m2·s)时,壁膜的质量通量占优,壁膜倾向于铺展流动,壁膜流动开始出现转折性变化,随着时间推移,壁膜流动整体呈现连续流动现象。
■ 当质量通量增加为100、200kg/(m2·s)时,壁膜连续流动的规律愈发明显,并且在同一水平线上,在大接触角下的疏水性壁面上的壁膜厚度从左到右先变小再变大,即在左右俩侧边缘处的壁膜最厚。此现象的机理是在壁膜质量通量占优的情况下,壁膜整体呈现连续流动的规律,但由于壁面的疏水性,壁膜仍然存在收缩的趋势,故在边缘处的壁膜最厚并且流动速度最大。
不同接触角下壁膜的形态差异
如图14所示,给定质量通量为:20 kg/(m2·s),对比研究时间为300ms,壁膜/壁面接触角分别为75°和15°,图为壁膜流动的形态差异。
壁膜在疏水性和亲水性表面上的流动分别呈现壁膜分离溪流流动和连续流动的规律。此外,联系上文,对比壁膜在疏水性表面和亲水性表面上的连续流动现象,发现在同一水平线上壁膜在亲水性表面上呈现俩侧厚度小、中间厚度大的规律。
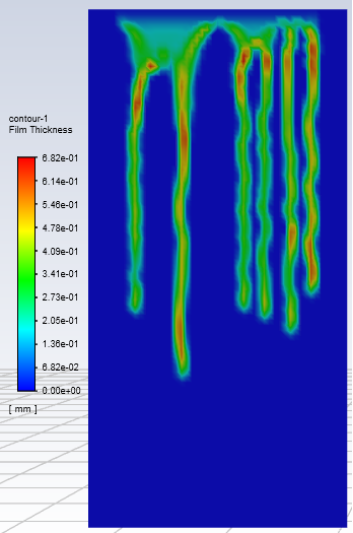
壁膜质量流:20 kg/(m2·s)
接触角:75°
时间:300 ms
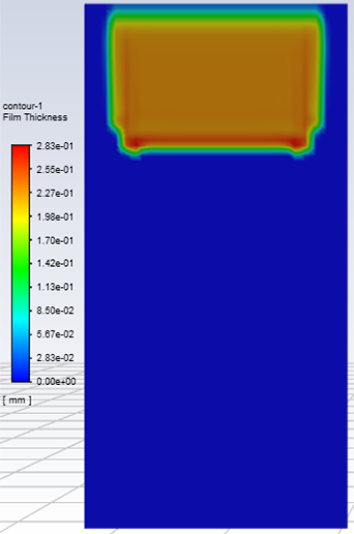
壁膜质量流:20 kg/(m2·s)
接触角:75°
时间:300 ms
图14. 同接触角下壁膜的形态差异
■ 壁膜模型还包含更多的子模型与相关应用,如可应用于喷淋冷却、灭火场景的拉格朗日壁膜模型建模、可应用于湿空气在冷壁面冷凝与再烘干过程的组分输运与欧拉壁膜模型的耦合建模。






