案例分享 | optiSLang:优化双频带缝隙天线
问题定义
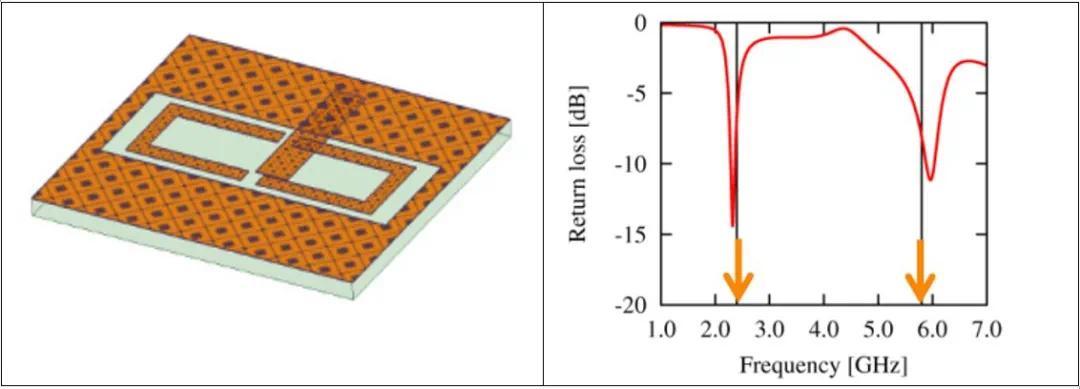
1. 最大限度降低频率在2.4和5.8GHz时的回波损耗
回波损耗的最小值(位置)与所需频率相匹配
两个最小值的振幅应最小化
2. 设计变量考虑9个几何参数
任务描述
缝隙的宽度和长度(ws, ls)
地平面上的U形导体与x方向和y方向上缝隙边界的距离(gap1, gap2)
地平面上两个导体之间的距离(dd)
地平面上导体在x方向和y方向的宽度(w1, w2)

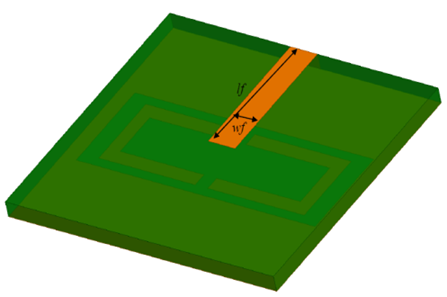
任务描述
微带馈线的长度和宽度(lf, wf)
Ansys Workbench工程
打开准备使用Workbench工程文件Dual_Band_Antenna.wbpz
使用Ansys HFSS(高频电磁场求解器)作为求解器
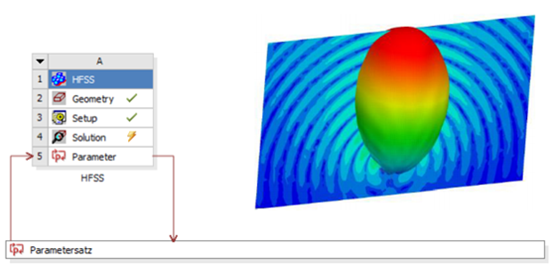
任务描述
响应值定义为预期频率(2.4与5.8GHz)的S11振幅以及两个最小值对应的频率
输入参数和仿真响应将出现在参数集中
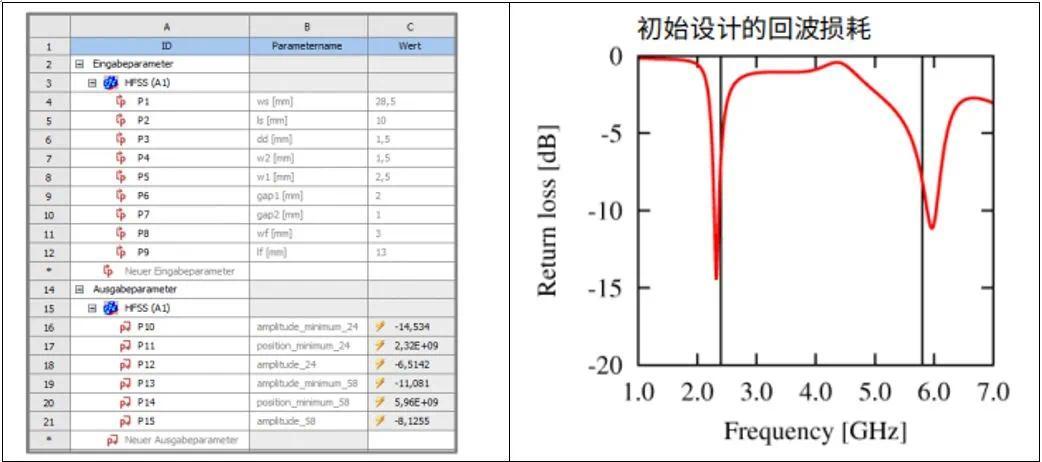
定义设计变量
将新的敏感度分析拖动到参数集上
指定几何参数的上限和下限
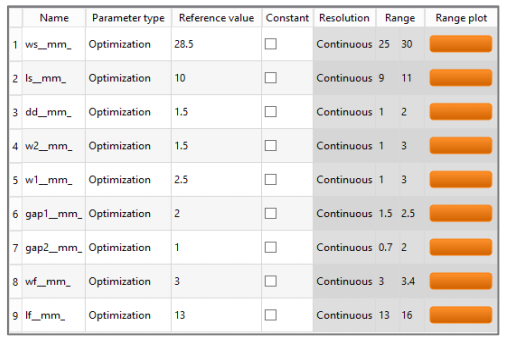
定义优化标准
将计算频率和期望频率的差值平方之和作为目标,监控敏感度设计中的偏差
约束是不必要的
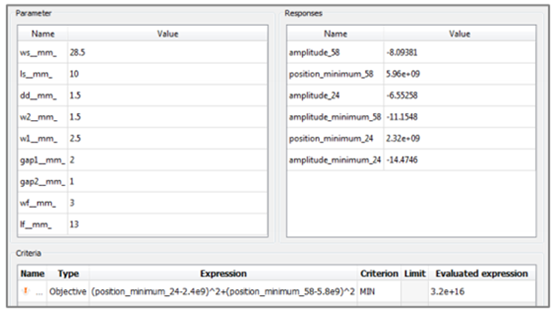
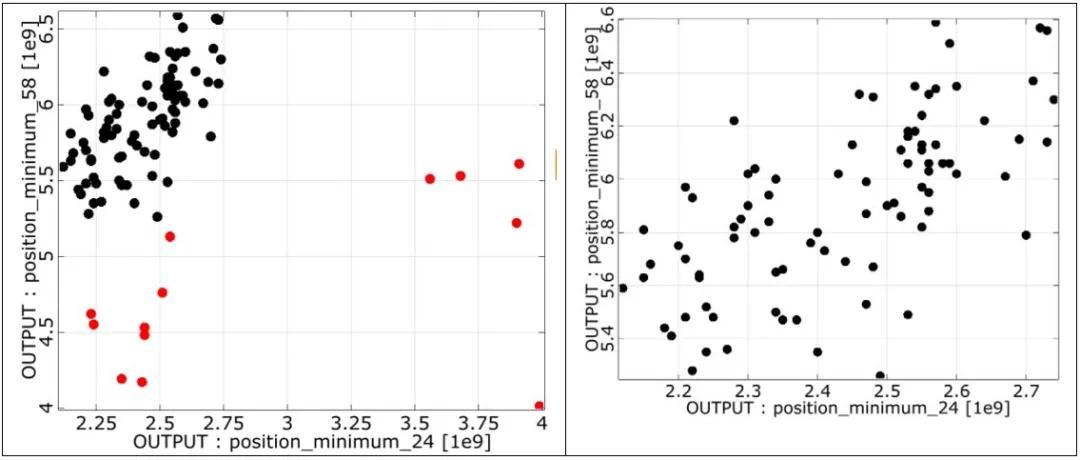
敏感度分析结果
使用HFSS求解器评估了100个拉丁超立方抽样(Latin Hypercube Samples)
一些设计频率与预期频率2.4和5.8 GHz相差甚远
不激活这些相差甚远的采样点后可在各位置上观察到正相关,此外MOP模型的预测质量也有所提高
使用MOP进行敏感度分析
1. 谐振点的位置主要受ws的影响,而且CoP值较高
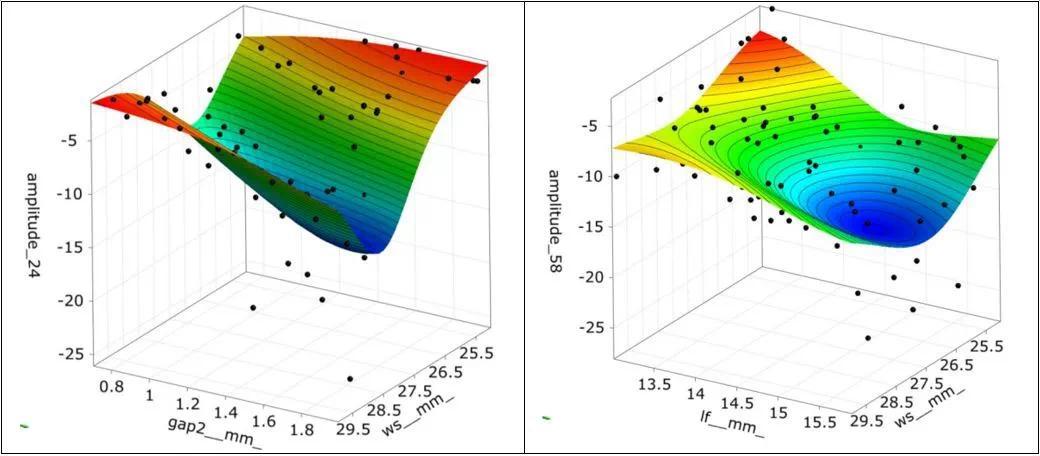
2. 参数ws和If对最小振幅的影响最大
3. 由于振幅的预测质量较低,因此无法对参数影响进行可靠量化
接下来的优化将考虑所有参数

使用MOP进行敏感度分析
谐振的频率位置显示出接近线性的行为,而且CoP值较大
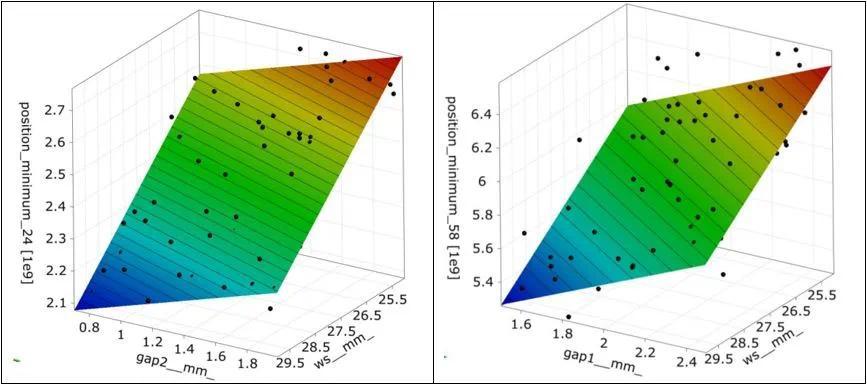
使用MOP进行敏感度分析
1.2.4与5.8GHz的S11振幅显示出强烈的非线性行为,而且CoP值较小
MOP上的直接优化可能不成功
下一步将使用直接求解器调用进行优化
敏感度分析的最佳设计
拉丁超立方体抽样的最佳设计表明,最小值的位置与预期值有较高的一致性
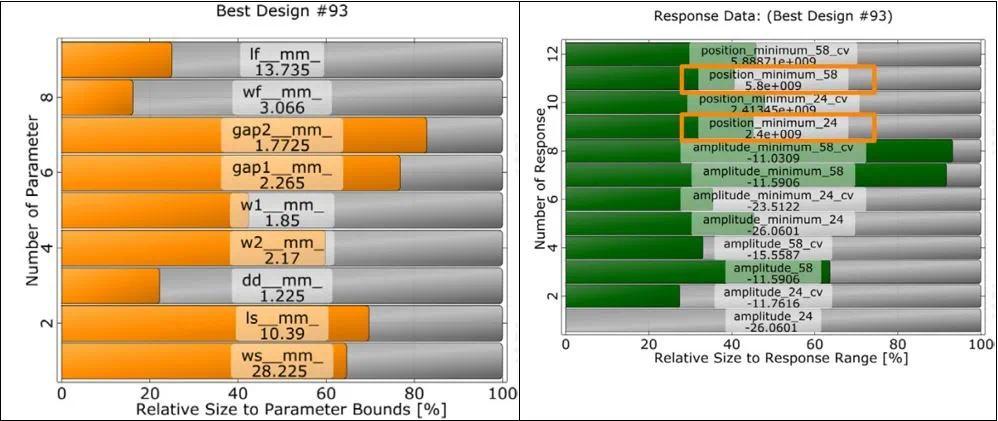
敏感度分析的最佳设计
1. 谐振点位置匹配比初始设计更好
2. 相应的振幅并未改善
接下来的优化必须考虑目标函数中的位置和振幅
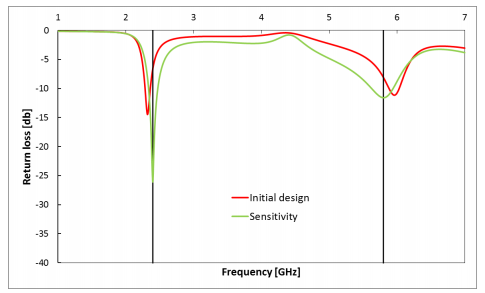
直接优化
1. 在目标函数中考虑以下两项和的最小化
谐振频率和预期频率的差值平方之和
两个预期频率对应的幅值的最大值
2. 通过将位置误差缩放0.01GHz引入加权

使用直接求解器进行优化
optiSLang建议使用自适应响应面方法作为优化方法
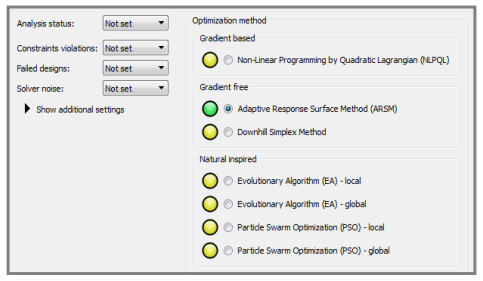
使用自适应响应面进行优化
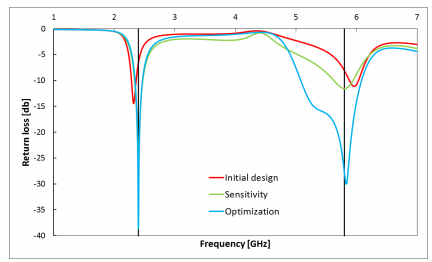
最佳设计与预期频率完美匹配,而且显著改善了振幅值
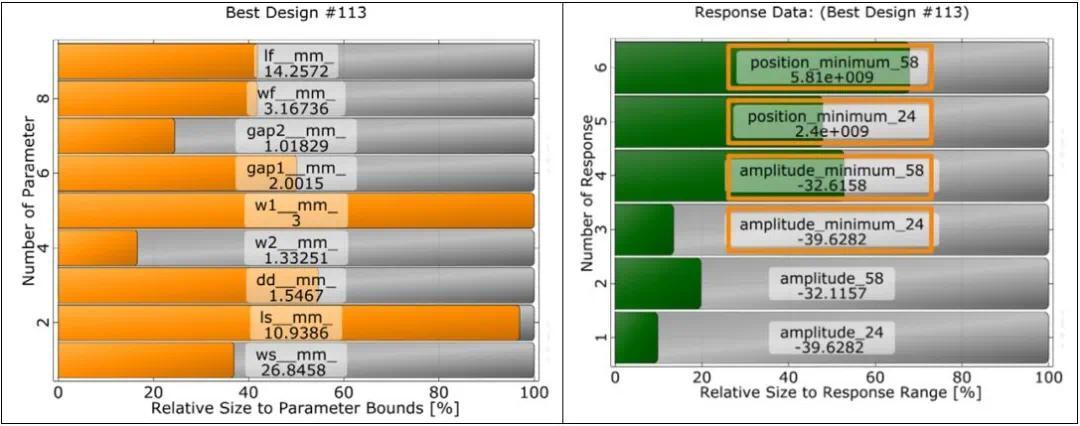
总结优化结果
敏感度分析发现了一种能够满足预期频率的设计
由于幅值中的CoP值较小,因此无法可靠地识别不重要的参数
通过加权频率偏差和振幅值,使用直接求解器进行优化,能够大大改善初始设计