数字信号处理v3 第三章 离散傅里叶变换(2)
继续讲解离散傅里叶变换。只讲实用的知识,不讲虚的。工程化的讲解有助于同学们消化理论知识。因为傅里叶变换本身就是一个实用化的技术。现在来讲讲傅里叶变换在实际使用的知识。同学们见过频谱仪吗?我们学校的学生肯定没有。因为直到2018年,我们学院都还没有这种设备。2022年了,也没有在实验室见到此设备。老师们难道不用吗?说句实话,很多老师只知道念PPT,连数字信号处理的应用都不讲解,那如何能让学生感受到本门课程的优势呢?哎,无奈,继续接着上堂课的内容开始讲解。目前市面上的频谱仪基本有两种,一种是FFT式频谱仪,另一种是扫频式频谱仪。后者基本已经被淘汰。本课程后续会讲到FFT,就是快速傅里叶变换,基于这种原理的频谱仪就是FFT式频谱仪。频谱仪的工作原理很简单,信号输入后经过滤波器给到ADC进行采集,将采样点记录下来,然后再通过DSP或者CPU完成FFT的运算就能得到信号的频谱。扫频式频谱仪是当年模拟时代的产物,在数字时代,这种频谱仪已经被淘汰!可以明确的告诉大家,信号处理的工作肯定离不开频谱仪,还有一种设备也离不开!那就是示波器!一般高校里面肯定有示波器,大家多用用就能知晓这些设备有哪些作用!最直观的感受就是通过频谱仪看信号的频域,通过示波器看信号的时域!傅里叶变换是一种精准的数学描述。但在计算机或者芯片中的实现过程却是需要一步步把时域和频域进行离散化的处理,而后进行大量的计算,最终给出结果。
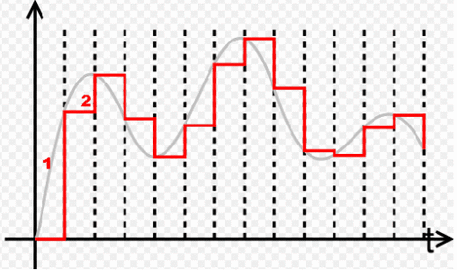
离散化也就是要采样结果。对信号在时域进行等间隔采样,那么信号在频域会发生周期延拓。同样道理,频域采样,自然时域也会发生周期延拓。那么要得到时域频域都离散的结果,显然时域频域都要采样。周期延拓怎么办?只取一个周期就行了。怎么只能取一个周期,求助于滤波器了。
总结一下运算的演化过程:
第一步,时域离散化,得到离散时间傅里叶变换(DTFT),频谱被周期化;
第二步,再将频域离散化,得到离散周期傅里叶级数(DFS),时域进一步被周期化。
第三步,考虑到周期离散化的时域和频域,只取一个周期研究,也就是众所周知的离散傅里叶变换(DFT)。
DFT是没有实际的物理意义,它可以满足我们研究的需要。借此运算,计算机的处理才成为可能。那什么是离散傅里叶变换?下面就讲到了!请同学们务必掌握DFT的概念和用法(DFT实质:有限长序列的傅里叶变换进行的有限点的离散采样)。
在频域分析信号分两种方式。第一种为对确定性信号进行傅里叶变换,分析频谱信息。第二种呢?随机信号的傅里叶信号不存在,转而研究它的功率谱。功率谱是定义为时域信号傅氏变换模平方然后除以时间长度。功率谱是随机过程的统计平均概念,所表现的是单位频带内信号功率随频率的变换情况。本公众 号中有关于谱分析的文章,欢迎学习交流这个系列文章!有些工程化的知识必须提及!比如截断效应!信号的截断效应是指在对信号进行处理时,由于对信号进行了截断操作而引起的一系列现象。一、截断的原因
在实际应用中,我们通常只能处理有限长度的信号。例如,在数字信号处理中,由于计算机的存储和计算能力有限,我们只能对有限长度的信号进行分析和处理。因此,需要对无限长的信号进行截断,得到一个有限长度的信号段。二、截断的方法
常见的截断方法有矩形窗截断和其他窗函数截断。矩形窗截断是最简单的截断方法,即将信号在某个时间区间内的值保留,而在该区间外的值设为零。其他窗函数如汉宁窗、海明窗等,可以在一定程度上减少截断带来的不良影响。窗的内容后续会讲解。三、截断效应的表现
- 频谱泄漏:截断后的信号的频谱不再是原信号频谱的准确表示,会出现频谱扩展的现象,即频谱泄漏。这是因为截断相当于将信号与一个矩形窗函数相乘,而矩形窗函数的频谱是一个 sinc 函数,具有无限宽的频谱,导致原信号的频谱在截断处发生泄漏。
- 频率分辨率降低:截断后的信号的频率分辨率会降低。频率分辨率是指能够分辨出的两个相邻频率成分之间的最小频率间隔。截断会使信号的频谱变得模糊,从而降低了频率分辨率。
四、减少截断效应的方法
- 选择合适的窗函数:不同的窗函数具有不同的频谱特性,可以根据信号的特点选择合适的窗函数,以减少频谱泄漏和提高频率分辨率。
- 增加信号长度:在可能的情况下,增加信号的长度可以减少截断效应。因为信号长度越长,截断对信号频谱的影响就越小。
- 采用其他信号处理方法:如频率抽样法、快速傅里叶变换(FFT)的补零技术等,可以在一定程度上减少截断效应。
这方面的内容就讲到这,关于之前提到的谱分析内容可以学习下面的文章。如果时间越长,那么图c就会越接近图b。大家可以写一个截断效应的仿真程序来加深这个概念。学完本章后,希望同学们能够利用DFT(在Matlab中使用什么函数呢?如果没有,大家可以根据定义写出DFT函数吗?)进行信号检测和谱分析。实践一次,胜过看书百遍!
考研测试!
这里搜集了部分历年考研中出现的关于离散傅里叶变换(DFT)的真题类型及示例,当然也有解答!
一、DFT 的基本定义与计算













.jpg?imageView2/0/w/120/h/120)
.jpg?imageView2/0/w/90/h/90)