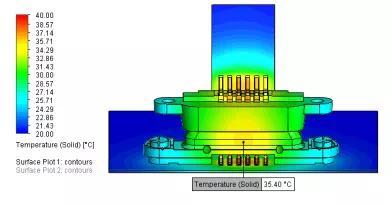
温升对称模型的简化

4年前浏览4422

在“[FloEFD] 网格划分对分析精度的影响中”，我们曾经提到：网格的多少/质量对计算结果精度有很大的影响，甚至可能会引起分析结果的失真。但是由于分析时效性及计算资源的限制，不能一味的追求细化网格，在此背景下对称模型的简化处理就能发挥一定的作用。

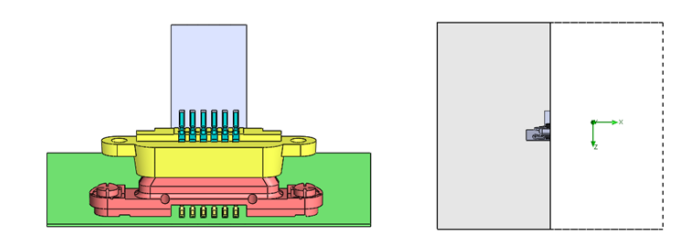
Figure-1 :对称模型

以图示模型为例进行对比说明：

对称模型设置与整体模型基本一致，不同的是计算域需要进行调整，如上图：

Case-1:对整体模型划分网格，采用局部网格进行网格细化。

Case-2:对一半模型划分网格，使网格质量与Case1相近。

对比以上两种模型运行时间及分析结果。

网格数及划分时间

Case-1

Case-2

Cell：640,101

Solid cell：250,082

Time：76s

Cell：263,421

Solid cell：92,612

Time：33s

运行时间及分析结果

Case1

Results:

探测点1 ：35.40℃

CPU Time：0:38:17

Case2

Results:

探测点1 ：35.38℃

CPU Time：0:09:43

总结：

① 在Cell总数及质量相近时，半模型所需计算资源将缩减很多，并且模型越复杂，效果则越明显，而结果基本相同。

② 若将半模型继续细化，则可以利用与整模型相同的计算资源得到更精确的结果.

对称模型注意事项：

1.如果在对称平面穿过的开口、表面或体积处指定整体边界条件（如质量流量或体积流量、热功耗），则必须将输入值调整为对称条件。Flow Simulation 会自动将指定值应用于计算区域。由于对称条件减小了计算区域和体积，因此必须相应减小其他条件（表面或体积）的指定值。例如，如果对称平面将开口分为两半，那么必须指定实际质量/体积流量的一半以满足条件。

2.不仅模型需要对称，边界条件及整体流体流动也要对称。

有时模型和入口流动均对称并不能保证其他流动区域也对称，例如通过圆柱面的冯卡门涡街。