信号完整性-我的均衡之CTLE学习笔记
本文摘要(由AI生成):
本文主要介绍了CTLE均衡技术在ADS通道仿真中的设置及仿真问题。首先介绍了通道对信号的频域和时域上的影响,包括差分线损耗曲线、时域脉冲信号的电压响应曲线以及频域上的输入输出电压频谱分量差异。接着介绍了CTLE的功能及其实现方式,包括有源CTLE和无源CTLE。最后介绍了在ADS中如何设置CTLE的参数,包括zeros、poles和pre-factor,并通过一个单零点和单极点的简单滤波器示例,分析了其频域响应和幅频响应。1、写在前面
相信大家在进行信号完整学习时,遇到的最大的困惑就是不知道何从下手,当初我也跟你们有同样的困惑,这也是我写这篇文章的目的之一。一是希望自己的学习过程有个记录,通过文章来整理自己的思路;二是希望这篇文章对你有一点帮助。
如何利用软件进行上手操作,能够进行基本的仿真设置,忽略背后那一堆公式的推导,快速地得出评估结果是非常重要的,这就是工程思维。当然,在这之后你仍然需要去理解背后的原理,只有这样才能提高自己的水平。
但是而对于初学者而言,最大的困难就在第一步。今天我要跟大家分享的是关于CTLE的均衡技术在ADS通道仿真中如何设置以及仿真的问题。
对于CTLE相信大家都听过,资料上应该也看过,但是若要问怎么设置CTLE的参数,这些参数代表的意思是什么估计会难倒一片,再问拉普拉斯变换又是什么,估计直接晕倒在厕所了………
好了,言归正传,在进行CTLE介绍之前首先介绍一下通道对信号的频域和时域上的影响。
二、通道的频域与时域特性
考虑一段长距离传输线,会对信号会带来什么问题呢?我们可以从频域和时域上来分析。如图所示,一段长10英寸的差分线,随着频率的提高,S21基本是线性增大的,在12.5GHz处的插损达到了17dB。
再看时域特性,输入信号原本是一个理想的方波,经过这段长距离走线后,输出电压的幅度降低了,同时上升沿和下降沿变的很缓慢,特别是下降沿有拖尾现象,这会对邻近的符号造成干扰,即我们常说的ISI(码间干扰)。
ISI的本质是通道对高频分量的衰减远大于低频分量的衰减。如果从传输线的等效LC模型来看,就是电容和电感负载对信号的影响。电容和电感都有一个充放电的时间,因此会使得上身沿和下降沿变缓。


8英寸长的差分线损耗曲线
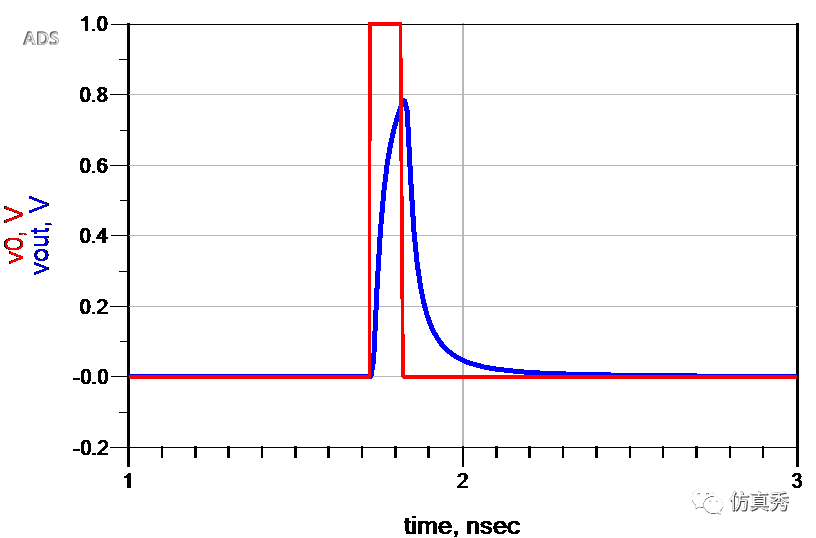
10英寸长的差分线对时域脉冲信号的电压响应曲线
如果进一步研究,我们再回到频域,如下图所示。输入电压的频谱分量和输出电压的频谱分量有很大区别。在10GHz以内,两者的频谱分量幅度差别不是很大,大约在5dB以内,但是随着频率的提高,输出信号的频谱分量幅度和输入信号之间的差距越来越大,在图中的4个mark点分别是11dB---16dB-----20dB-----23dB。
也就是说,通道对高频分量的衰减远大于低频分量,而且随着频率的提高,这种差距是越来越大,这是造成ISI的根源。

输出电压与输入电压的频谱图
三、通道对眼图的影响
高速信号都是以眼图来评估其质量,那么试想一下,如果一个25Gbps的信号经过这段长走线,其眼图会是什么样呢?这可以通过在ADS中搭建一个简单的通道仿真来看,如下图所示。TX是信号源,速率是25Gbps,中间经过一段8英寸长的差分线传输线,到达接收端RX元件,通过眼图探针测量收端的眼图。
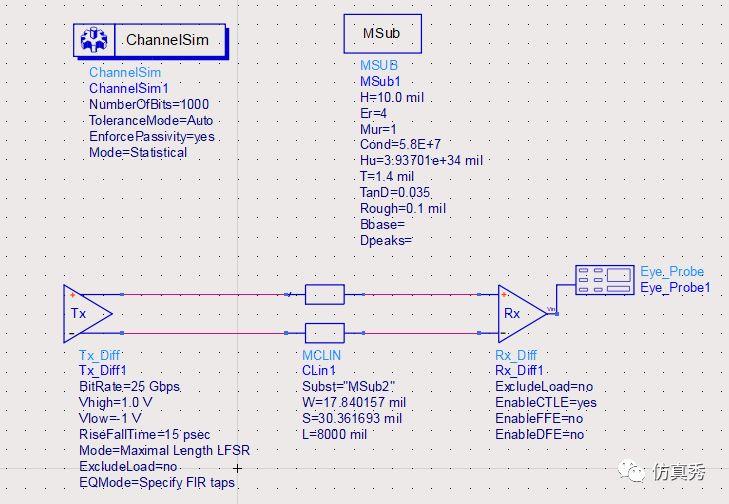
通道仿真原理图
启动运行按钮,仿真结果如下图所示,我们看到收端的眼图已经完全闭合,带来了非常严重的信号完整性问题,如果收端不做任何处理,那么接收端收到的信号将全是误码。

CTLE关闭
而当把收端的CTLE功能打开时,神奇的一幕出现了,如下图所示,原本闭合的眼图张开了,眼高达到了402mV。是不是很兴奋?兴奋的是不是想了解CTLE是个什么东西。
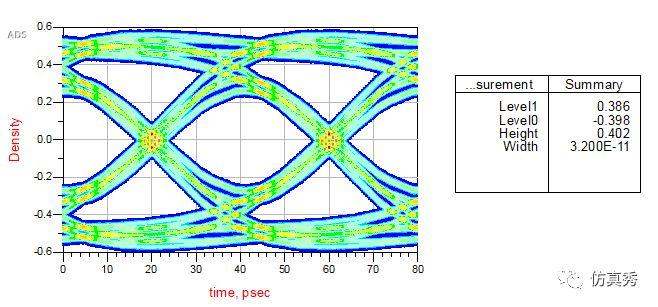
CTLE 开启
四、什么是CTLE
到这一步我们看到了CTLE功能的神奇,能够将原本闭合的眼图打开,也就是说能够消除ISI的部分影响。那么CTLE究竟是什么呢?
CTLE是Continuous Time Linear Equalization的简称,即连续时间线性均衡器,是在高速串行接收链路中常用的一种均衡技术。
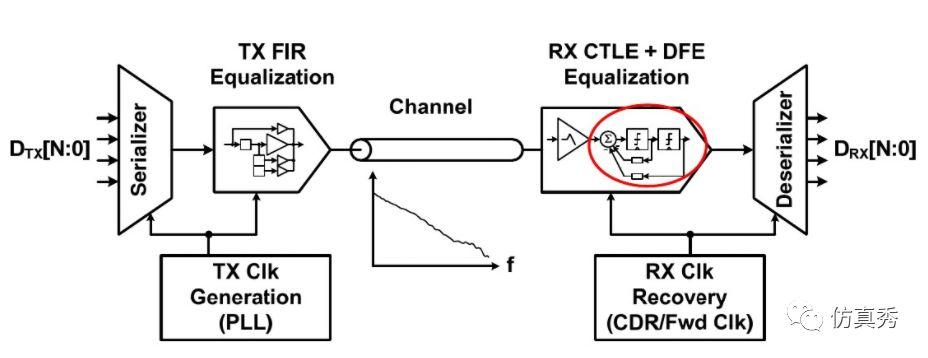
典型的高速串行收发链路架构
CTLE本质上是一个高通滤波器,实现方式有无源和有源两种方式。(不想看公式的可以忽略)
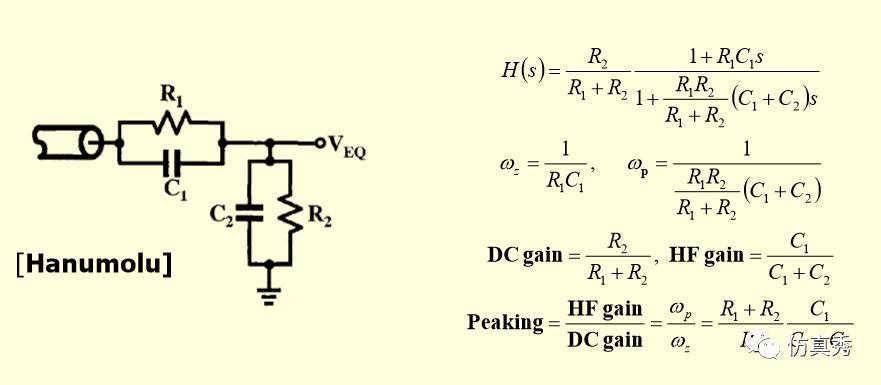
无源CTLE的实现
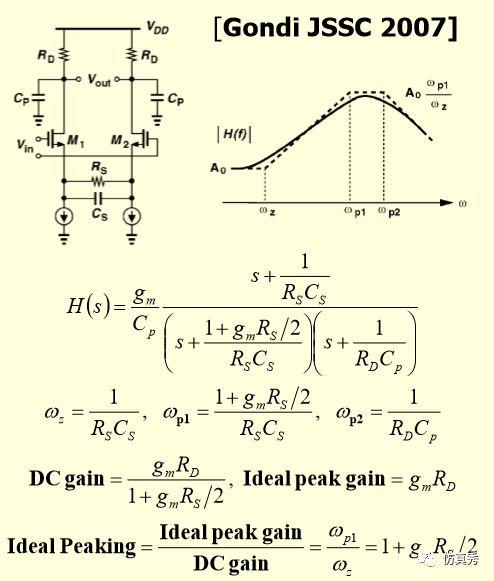
有源CTLE的实现
5、ADS中的CTLE及参数设置
那么在ADS中该如何设置它的参数呢?在ADS中的通道仿真中,对于RX元件有CTLE、FFE、DFE三种均衡设置方式。如下图所示:

通道仿真中的RX元件
勾选Enable,点击Edit按钮,出现如下对话框,有zeros和poles,pre-factor。这是什么鬼东西呢?大家都听说过CTLE本质上是一个高通滤波器,这里的Zeros和poles分别是这个高通滤波器的零点和极点,也就是前面那些公式里面出现的wz和wp,pre-factor是滤波器传递函数的系数。

Zeros和poles
对于高通滤波器,做过射频的都知道,以前都是通过设置其3dB带宽,截止频率和衰减等指标可以获得一个高通滤波器。比如下图所示,就是一个截止频率为0.8GHz,3dB带宽是1GHz的巴特沃斯高通滤波器,其频率响应曲线如下图,含义非常的清晰。

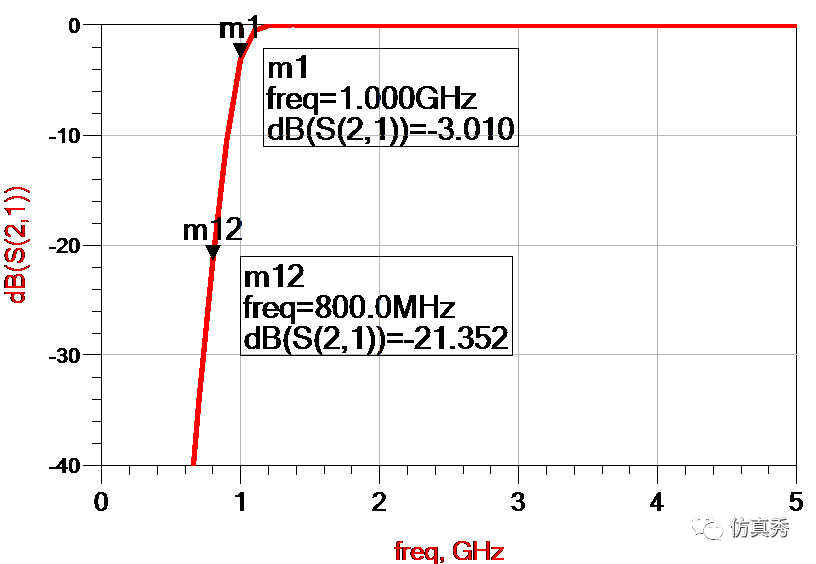
巴特沃斯高通滤波器
而在这里,不是这样设置的,高通滤波器的特性是通过零点和极点来控制的。以前习惯于频域上的设置,现在是时域上的设置方法。如果要进一步了解零点和极点的概念,你需要去了解滤波器的传递函数和拉普拉斯变换(估计会晕倒一大片……….),这在后面进一步讲。
好了,言归正传,到这里大家想知道的就是我如何在ADS仿真中,设置一个CTLE的参数来提高信号质量,以便应用于我们的实际项目中,节约调试时间。以这个通道仿真为例,CTLE的参数设置如下:
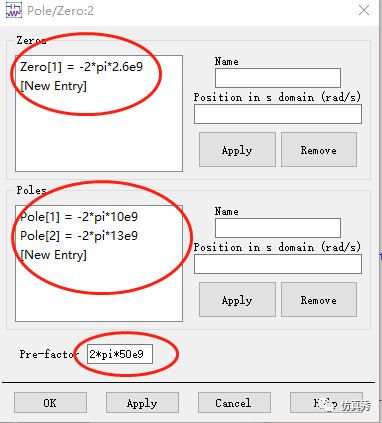
CTLE参数设置
零点和极点的单位是rad/s,不是Hz,因此需要设置成角频率的形式,而且是负数,即w=-2πf。在ADS中,CTLE的传递函数公式如下
H(s)= Pre-factor*N(s)/D(s)
其中
N(s)=(s-Zero[1]) * (s-Zero[2]) * ...
D(s)=(s-Pole[1]) * (s-Pole[2]) * ...
Zero[1]、Zero[2]、Zero[3]…. Zero[n]代表n个零点,Pole[1]、Pole[2]、Pole[3]….. Pole[n]代表n个极点。
当传递函数的分子为0时对应的频点就叫零点,当传递函数的分母为0时对应的频点就是极点。
本例中由1个零点和2个极点构成,还有一个前置系数。写成传递函数的形式就是
H(s)= Pre-factor*(s+wz0)/(s+wp1)*(s+wp2)
其中,wz0=-2*pi*2.6e9,wp1=-2*pi*10e9,wp2=-2*pi*13e9。
Pre-factor=Adc*wp1*wp2/wz0,在ADS中,Adc默认取1,正常是在[0,1],代表了频率为0时的直流增益。
也就是说零点对应的频率为2.6GHz,极点1对应的频率为10GHz,极点2对应的频率为13GHz,所以前置系数Pre-factor=2*pi*50e9。那么这里我们要追问两个问题:
第一、参数设置对应的频率响应是怎么样的?
第二、为什么CTLE能够使眼图张开?
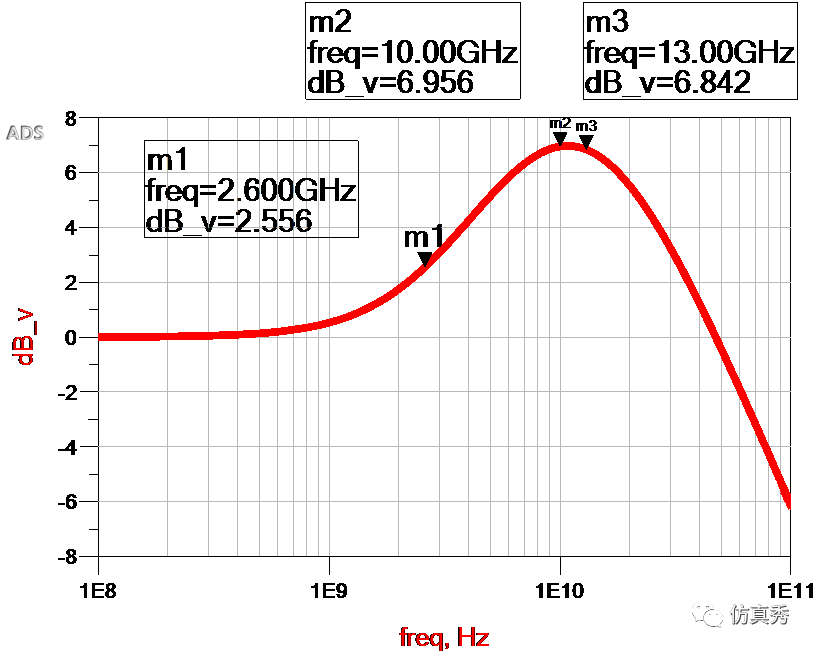
CTLE的频率响应
如上图所示,就是上述CTLE的频率响应曲线。我们看到这条曲线其实前半部分是一个高通滤波器,后半部分增益又是急剧下降的,这跟我们传统的高通滤波器是不一样的,如上图那个的那个巴特沃斯高通滤波器。就这条曲线本身来说,其实更像是一条带通滤波器。
正是因为CTLE利用的就是前半部分的高通特性,所以习惯上就称CTLE为高通滤波器。另外从图中还可以看出,大概在1GHz以后滤波器的增益开始有明显的增大,1GHz以内增益基本都是保持不变的,大概在11GHz附件增大到peak值7dB。然后又开始急剧衰减。
而且我们发现,零点和极点并不完全对应图中的频率拐点。比如零点我们设置的是2.6GHz,但是频率从1GHz以后就开始往上拐了。两个极点10GHz和13GHz也不是对应图中的增益peak值,而是处于peak值的两边。但有一点可以肯定,零点和极点一起控制了这条曲线的形状。
再比如,在USB3.0中,CTLE的传递函数和频率响应曲线如下所示,从图中我们也可以看到类似的规律。
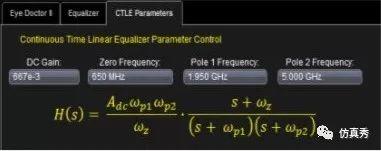
USB3.0-CTLE传递函数
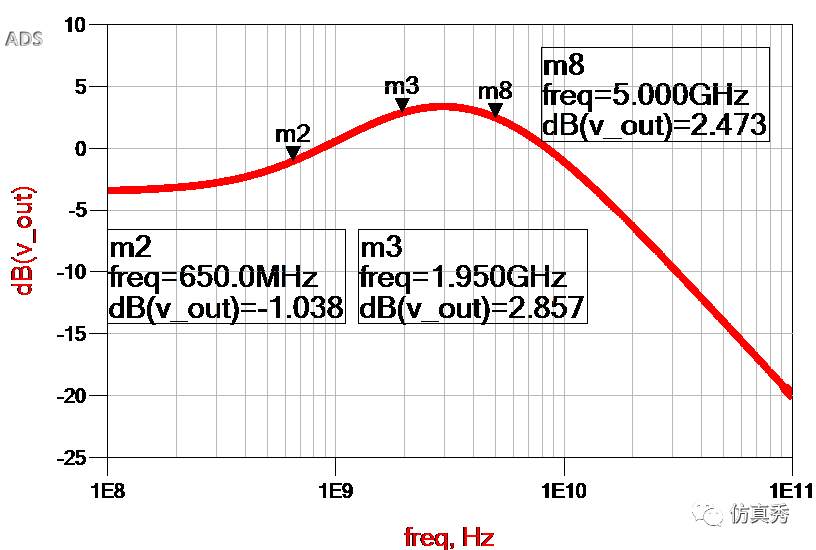
USB3.0 CTLE频率响应曲线
六、为什么CTLE能够改善眼图质量
在解决了怎么设置CTLE的问题之后,作为一个对技术有追求的工程师,我们需要多问几个为什么。那就是为什么CTLE能够改善眼图质量?
既然CTLE是一个通过零点和极点控制的高通滤波器,那么信号经过CTLE之后的频率响应会是什么样的呢?
如下图所示,紫色为无CTLE时的通道频率响应,蓝色为打开CTLE之后的通道频率响应,红色为CTLE本身的频率响应。从图中可以看到,蓝色曲线在低频处(2GHz以内)与紫色曲线基本重合,但在2GHz以后直到30GHz范围内,蓝色曲线都在紫色曲线的上方,这表明在高频处,蓝色曲线的衰减比紫色要小。
在CTLE的作用下(红色),紫色曲线被拉升了一下,使得紫色移动到了蓝色位置,其增益平坦度比原来要好。
若从带宽的角度来看,以3dB带宽为基准,在没有CTLE的时候,带宽只有2.1GHz,打开CTLE之后带宽可以达到6.6GHz,提高了3倍。换句话说,CTLE相当于提高了通道的带宽,这就是为什么CTLE能够使眼图睁开的本质原因。对,因为它提高了通道的带宽。
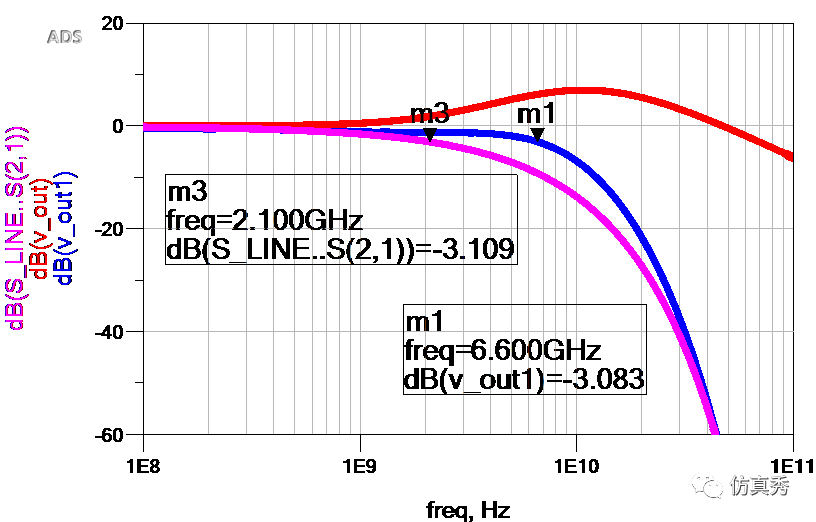
有无CTLE时的频率响应曲线对比
从CTLE的频率响应曲线我们看到,CTLE是对其中某一段频率范围的信号进行选择性放大,而对这段频率范围以外的信号又是衰减的。因此,可以再从时域上验证一下。当输入一个正弦信号,频率为1GHz和10GHz时,经过CTLE之后,其时域波形分别如下图,红色代表输入信号,蓝色代表输出信号。从图中可以看出,在1GHz时,信号幅度基本相等,没有放大,而在10GHz时,信号幅度放大了2.2倍,转换成dB就是6.9dB,与上图中的频率响应曲线是对应的。
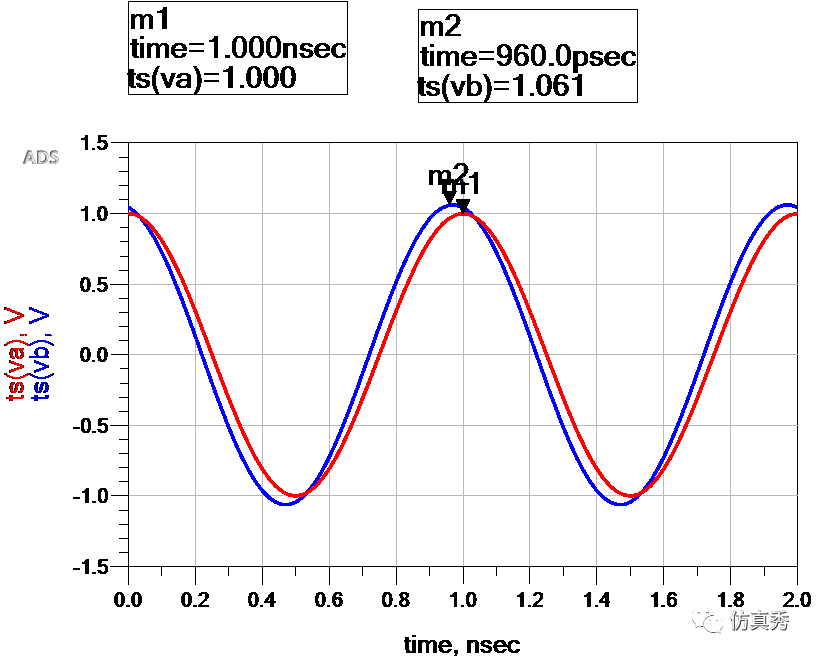
1GHz正弦波输入
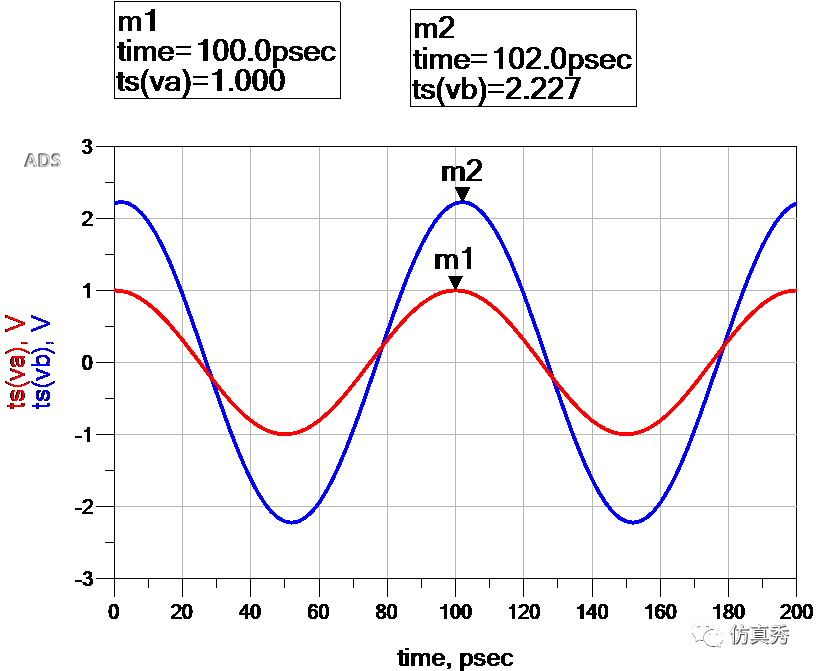
10GHz正弦波输入
七、总结
以上我们利用ADS软件分析了传输线通道衰减带来的ISI问题,并通过通道仿真发现ISI对眼图恶化非常严重。
在本例中,对于25Gbps的信号来说,8英寸长的传输线已经使得收端眼图完全闭合。在收端采用CTLE的均衡技术之后,眼图重新张开。
于是对收端CTLE的均衡技术进行了介绍,并解析了如何在ADS中进行参数设置。并从频域的角度分析了为什么CTLE能够这么神奇,其本质是提高了通道的带宽。
附录A:关于零点和极点的物理意义
上文说道零点和极点一起控制了CTLE的频响曲线的形状,那么他们之间到底是什么关系呢?这需要从零点和极点的物理意义说起。
下面是知乎上关系滤波器零点和极点问题的回答,我觉得解释的比较清楚,这里我偷个懒,就直接**过来,供大家参考,写的非常的清晰明了。
在学习信号与系统的过程中,我们都会被灌输一个概念:实际当中的绝大多数系统都可以用分式多项式形式的系统函数加以表示。这里我们不加证明地全盘接受这一概念(实际上,这个假设我们是可以接受的,联想泰勒级数)。那么我们我们可以将系统函数表示成:

你发现我这里直接用Laplace变换了,是的没错,就是这样。。。
我们可以作出相应的零极点图:
我们再画一个简单一点的。

我还是觉得太烦了!
所以最后我们就拿这个举例子:
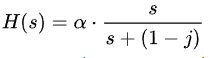
a是啥?现实中不是一般不存在单复零、极点的系统么?管他呢。。。
这是一个最简单的单零点和单极点的系统。我们要判断这个滤波器是高通、低通、带通就至少要对这个滤波器的频域进行分析。我们根据Laplace变换和傅里叶变化的关系可以得到:

其幅度和角度响应分别为:
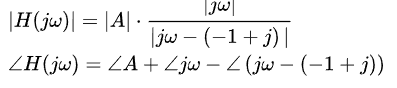
我们可以发现,其实幅频响应可以视为零点到频率点的向量的模值与极点到频率点的向量的模值的比值。也即,
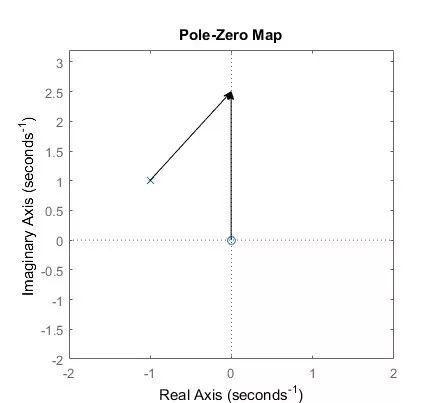
那么通过图形我们可以分析,当频率点jw位于无穷远时,两个矢量的模值近似相等,这时系统函数的值应当为H(s)=A(其实还是要稍微大一点点)。当频点从正无穷趋向于0时,两个矢量的模的比值逐渐增大,直到w=1时,H(j)=1,此时两个矢量的模值相等。
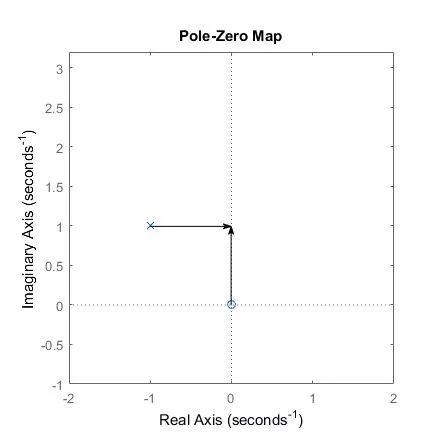
随着w=0,零点对应的矢量的模长逐渐趋近于0,直到H(j0)=0
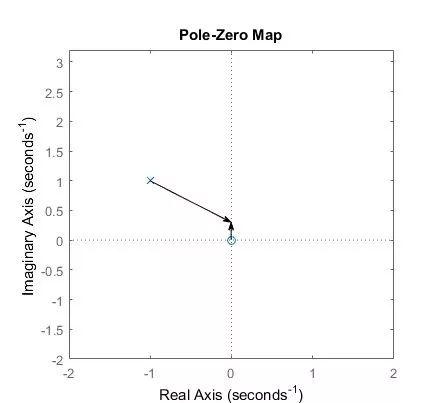

这样不精确,我们再用MATLAB跑一个
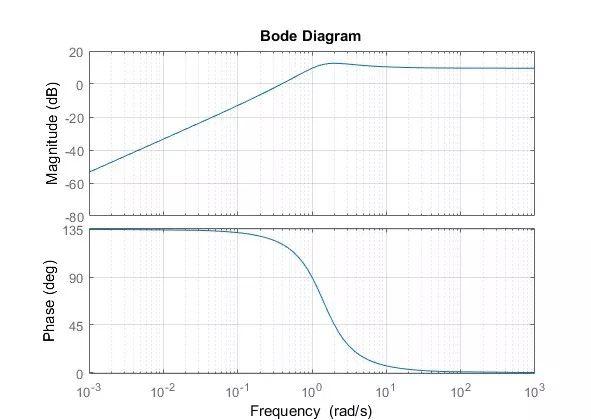
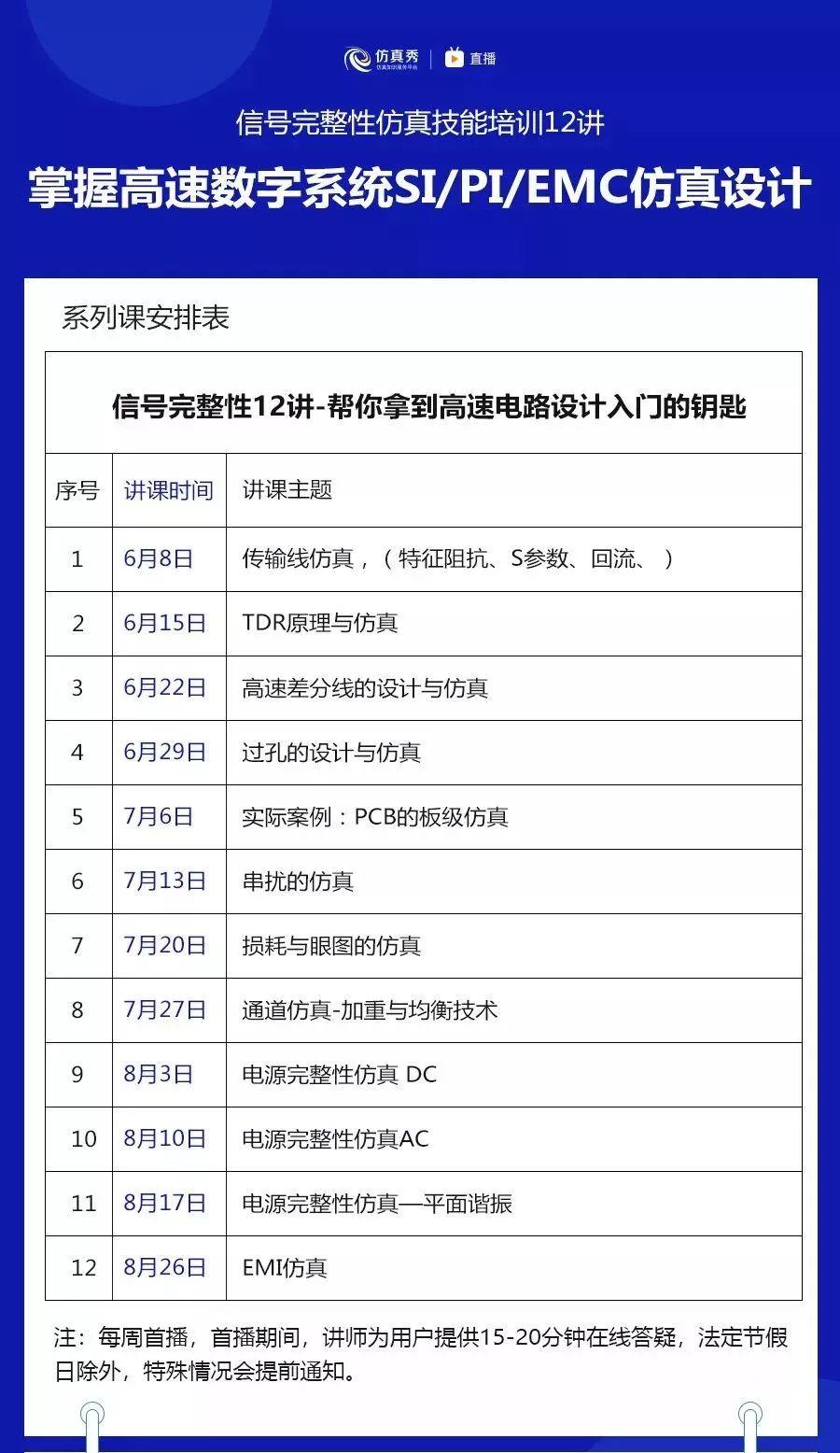
以上是笔者《均衡之CTLE学习笔记》希望对大家有所帮助,自2019年6月6日,受仿真秀平台邀请,我将在这里分享《信号完整性仿真培训12讲-帮你拿到高速电路设计入门的钥匙》,以下是课程排期表:
课程亮点(用户得到):
①掌握信号完整性的基本概念,结合仿真工具深刻理解基础理论;
②掌握ADS的信号完整性仿真流程和工具的使用;
③解决学员在信号完整性入门难、无头绪的问题;
④帮你拿到高速电路设计入门的钥匙;
⑤根据老师自身的项目实战经验分享实际案例,让你理解如何应对高速电路设计;
⑥ 所有听课用户,均可以加入申请加入ADS高频电磁交流群,抱团学习理论,软件和行业应用,课程结束后可以获得部分资料和模型。
⑦付费用户,可以及加入讲师个人的VIP学习群,与讲师持续交流。也可以联系小助手直接获得模型文件和资料。
作者:半个射频工程师 现任某光通信公司技术总监 仿真秀科普作者
声明:原创文章,首发仿真秀,部分图片源自网络,如有不当请联系我们,欢迎分享,禁止私自转载,转载请联系我们。






