电机定子模态的空间特征

节点是指模态振型值为零的位置，也就是说在振型动画中，不动的点即为节点，也是模态振型与原始未变形的结构的交点位置，并且每一阶模态的节点位置都不相同。反节点是指振型值最大的位置，不同模态的反节点位置也不相同。节点与反节点如图1所示。

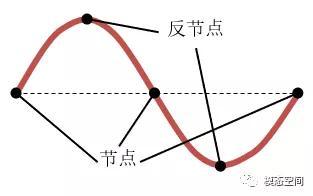
图1 节点与反节点

在一些文献中经常看到用mode（m,n）来描述模态的阶次，这两个数可能是指两个正交方向的节点数，也可能是指两个正交方向的反节点数。如对于二维平面类结构的某一阶mode (m,n)而言，m是指沿平面一个方向模态振型的反节点数，n是指平面内与前一个方向正交的方向的反节点数。如图2所示为某平面类结构按这种方式表示的模态。

mode (1,1) 

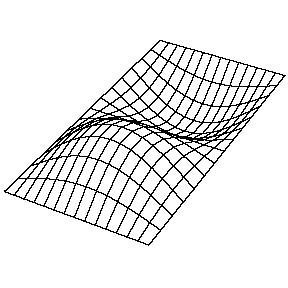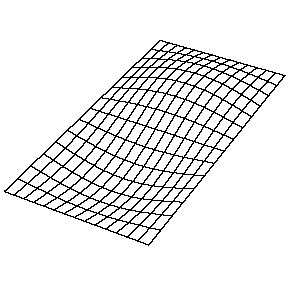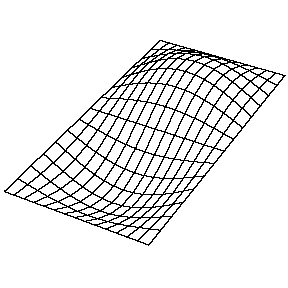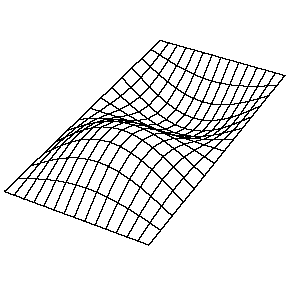
mode (1,2) 

mode (2,1) 

mode (2,2) 

图2 某平面类结构的模态表示方式

对于圆形、圆盘形或圆柱形结构而言，也用mode (m,n)来描述模态，但这些的m,n则分别指两个不同方向的节点（节圆或节径）数。如图3所示为某圆盘类结构的模态振型，此时m表示节径数，n表示节圆数。

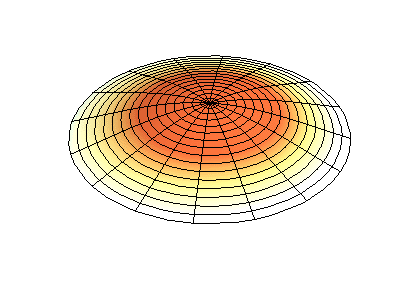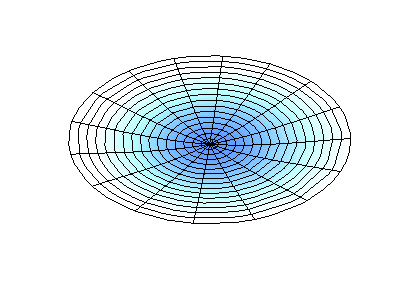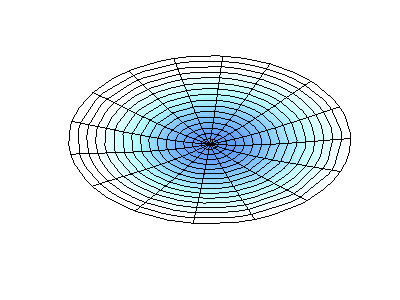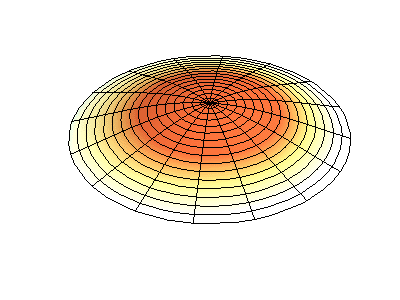
mode (0,1) 

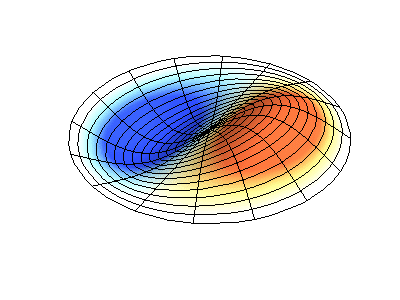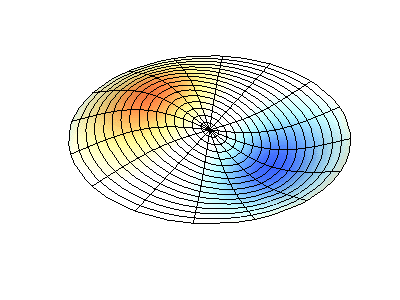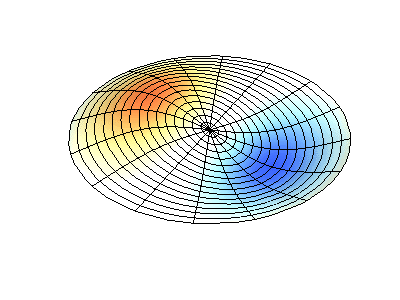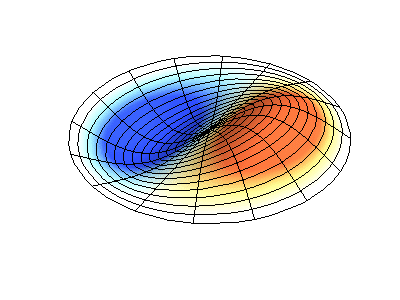
mode (1,1) 

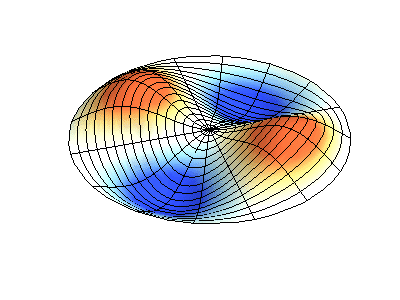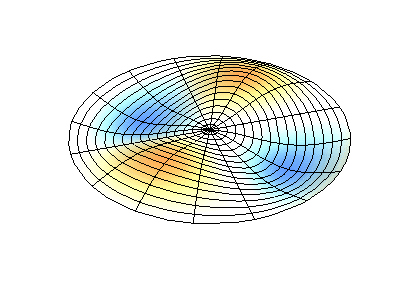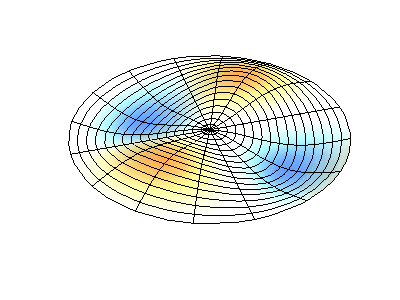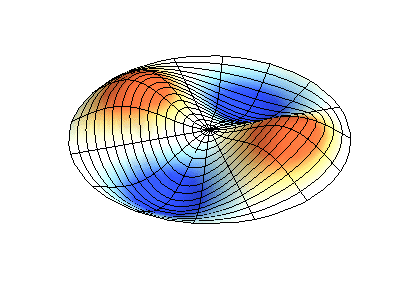
mode (2,1) 

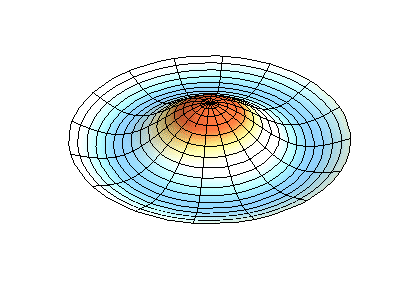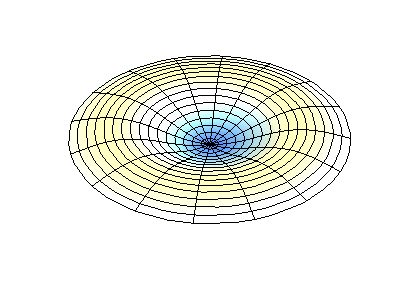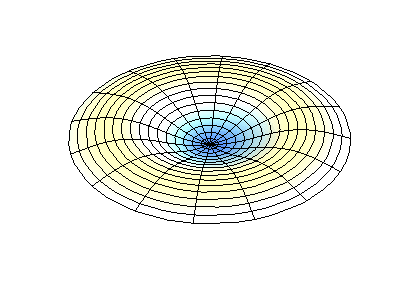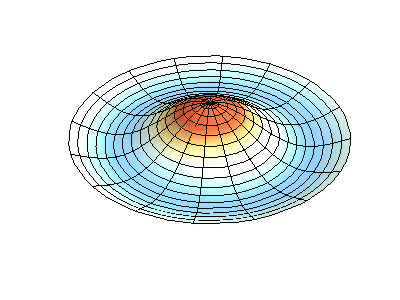
mode (0,2) 

图3 圆盘类结构的模态表示方式

3、电机定子模态的空间阶次

电机的定子是一个空心圆柱形结构，如图4所示，当用mode (m,n)来描述其模态时，m表示轴向的节点数，n表示周向节点数。但这里的n是周向节点数的一半，也可以认为n是径向的瓣数。周向各阶模态振型如图5所示，红色表示振型，黑色表示未变形图。

a)定子实物

b)定子FEM 

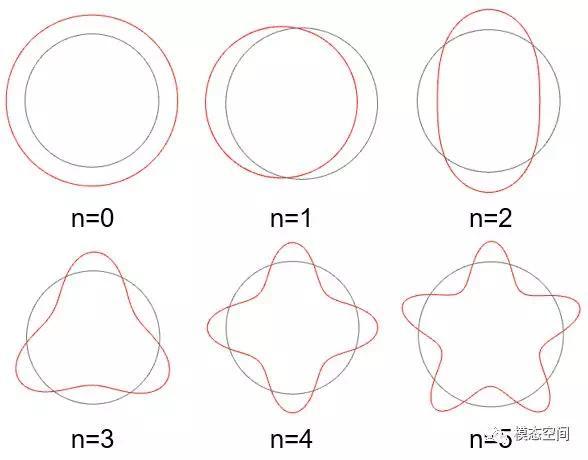
图5 m=0时，前6阶（n=0-5）模态振型

（图形由Simcenter 3D计算得到）

从图5可以看出，如当n=3时，周向节点数为6，但对应的模态阶次为3。因此，周向节点数的一半对应模态的空间阶次。或者也可以认为n所对应的模态空间阶次为相应振型的瓣数，如n=3的振型有3瓣。另一方面，按空间阶次排序时，各阶模态频率不再是按频率从小到大的顺序排列，图5中的0阶次对应的频率远高于5阶次的频率。如图6所示，n=0阶的模态频率为5338Hz，远高于后面的2，3，4阶模态频率，与按模态频率从小到大的传统表示方式明显不同。

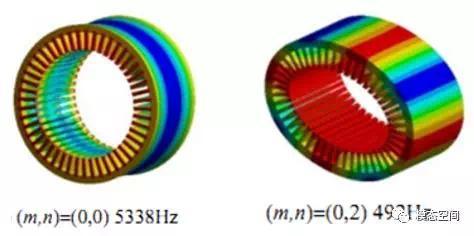
图6 各阶模态频率与模态振型

在图5中，n=1为刚体模态，n≥2为弹性模态，n=0是传统表示方式中的高频模态，由于它的振型是沿径向变大或缩小，因此，这阶模态也称为“呼吸”模态。由于电机定子为轴对称结构，因此，弹性模态还存在重根，如图7所示。

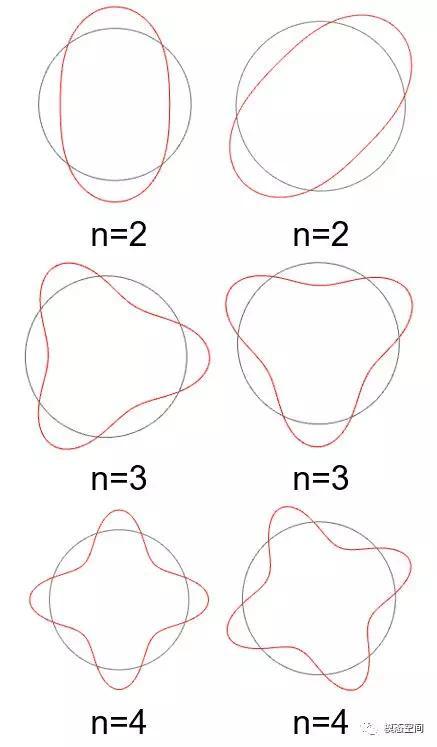
图7 电机弹性重根模态

（图形由Simcenter 3D计算得到）

以上描述的情况都是m=0时，也就是轴向无节点时的模态，但实际上，电机定子除了轴向无节点的模态之外，还有轴向有1个或多个节点的模态，如图8中的模态（1，2）和模态（1，3）。对于周向节点数相同的模态，轴向节点数m越高，频率越高，如图中的模态（1，3）的频率比模态（0，3）高725Hz。因此，周向节点数相同的模态存在无穷多阶，因为轴向节点数不同。

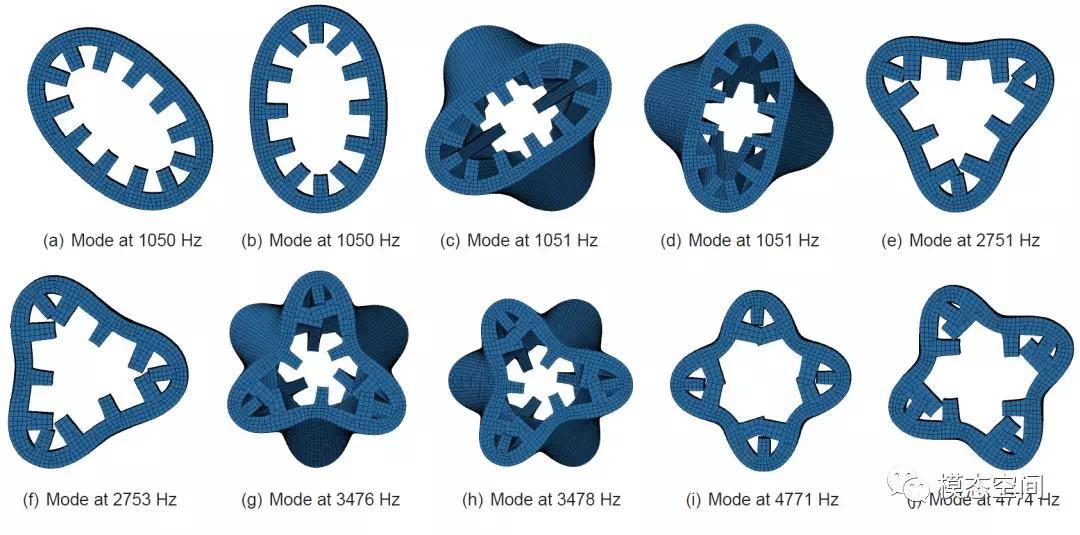
图8 电机定子的模态

4、关心轴向节点为0的低阶模态的原因

对于电机振动和噪声而言，比较重要的是研究轴向阶次为零，并以径向振动为主，且阶次较低的模态。这主要是基于以下两个方面的原因：

1）径向电磁力波p的空间前5阶次力波的形状如图9所示，这与电机定子前5阶模态振型完全相同或相似，因而，电机定子周向节点数的模态阶次与电磁力波的阶次定义相同。关于电磁力波是如何产生的，请参考朱碧华同学的文章《浅谈新能源汽车NVH：永磁同步驱动电机径向电磁力致噪声》。

在《什么是固有频率？》一文中讲到，当外界的激励频率接近或者等于结构的固有频率时，结构会发生共振现象。而对于电机定子而言，除了频率接近或相同之外，还需要考虑电磁力波的波形也需要与定子某一阶模态振型相近或相同。即当径向电磁力波某一阶次与定子空间模态振型相同，且电磁力波的频率与定子这一阶模态频率接近或相等时，定子会发生共振，因此，电磁力波需要从振型上和频率上与电机定子的模态阶次避开。

从两个方面来考虑，是基于周向节点相同的模态，因轴向节点数不同导致还存在无穷多个固有频率，也就是说，固有频率相同的模态可能对应多阶不同的模态。如图8所示的周向n=3的模态，当m=0的模态频率为1050Hz；m=1的模态频率为1051Hz，二者的固有频率非常接近。由于轴向节点和周向节点的不同组合，难免不存在固有频率相同，而节点数不同的模态。因此，避免电机共振问题，需要同时考虑频率和振型，也就是所谓的“避频”与“避型”。

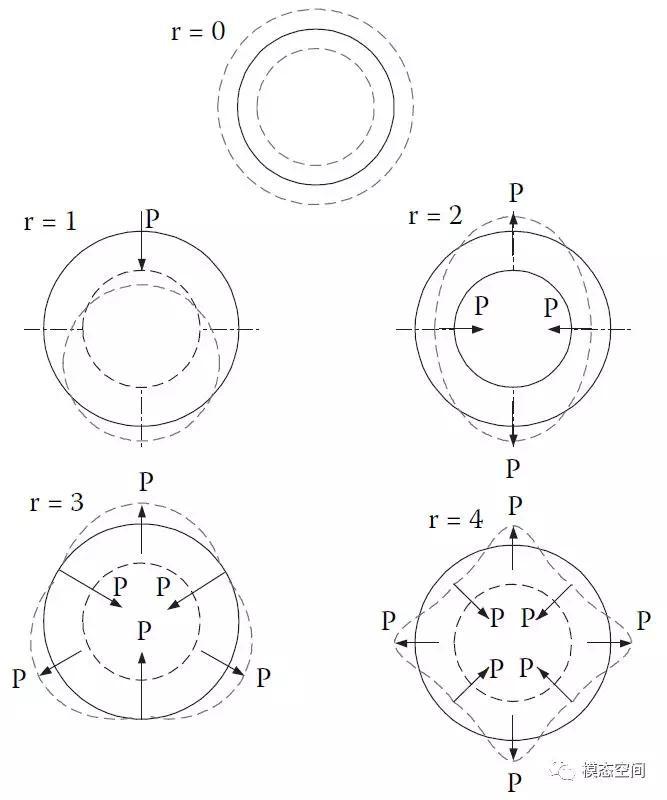
图9 电磁力波的前5阶波形

2）当仅考虑定子的周向模态时，定子铁芯的变形Δd与电磁力波阶次r的4次方成反比，即

Δd∝1/r⁴

从上式可以看出，电磁力波的阶数越高，产生的变形越小，因而，只关心低阶力波即可。

5、小结

通过上面的分析，对于电机定子模态，我们可以得出如下结论：

1）电机定子模态在空间上以轴向节点数和周向节点数的一半(或是径向瓣数)来表示。

2）周向节点数相同的模态，固有频率有无穷多组，因为轴向节点数可以不同。

3）周向节点数不同的模态，固有频率有无穷多组，分别对应径向电磁力波的分布形状，其阶次定义与径向电磁力波阶次相同。

4）轴向节点数不同的模态，固有频率有无穷多组，阶次等于轴向节点数。

5）轴向节点数为零的低阶模态是电机振动噪声关注的重点。

6）从避免共振的角度来讲，电磁力波需要从振型（力波形状与模态振型相近或相同）和频率（力波频率与模态频率相近或相同）上同时考虑避开。 

参考：

1.http://www.acs.psu.edu/drussell/Demos/MembraneCircle/Circle.html

2.MarlinO. Thurston. Noise of Polyphase Electric Motors. CRC Press, 2006

3.诸自强，陈永校. 电机噪声的分析与控制.浙江大学出版社，1987

作者：谭祥军 模态空间公 众号主编

声明：原创文章，首发模态空间公 众号（ID:modalspace），欢迎分享，禁止私自转载，转载请联系作者授权。