三维辐射绕射水动力计算程序Nemoh的精度验证
本文摘要(由AI生成):
本文验证了三维辐射绕射水动力计算程序Nemoh的计算精度。结果显示,Nemoh对网格大小敏感,细网格对小周期问题有利;在多体耦合水动力计算中,Nemoh与AQWA结果高度一致;但对于有月池结构物的波浪力计算,Nemoh精度有限。因此,使用Nemoh时需考虑网格影响,对于复杂问题应进一步验证其精度。
针对Nemoh的精度验证包括三部分:
水动力网格收敛性;
多体水动力计算精度;
特殊结构(有月池)的水动力计算精度验证。
01
—
网格收敛性
基于常数面元法的三维辐射绕射水动力计算程序依赖于水动力面元网格质量,网格越密,浮体外表面描述越精确,静水力计算精度越高,能够实现的水动力计算频率越高(周期越小)。
不同的计算程序对于网格的要求不尽相同,横向比较而言,WAMIT无疑是对水动力网格适应性最好的,更Robust。有一些计算程序(如AQWA)对于网格的质量会有严格的要求,计算网格在不满足内部网格质量要求的情况下无法进行计算,这些约束包括:单元大小与计算频率之间的关系(单元大小小于波长1/7),网格形态规整,网格节点连续等等。
Nemoh的程序内部对网格也有要求(单元大小小于波长1/7以及水深与波长的比等),但并不给出确切的提示,只要网格满足一般要求,程序可以进行计算,但精度会受到比较明显的影响。
这里以一艘MPV为研究对象,对Nemoh的网格质量对于计算精度的影响进行分析。
MPV主尺度信息如下[1]:
| 数据项目 | 单位 | 数据 |
| 吃 | m | 5.6 |
| 排水量 | ton | 6479 |
| 重心相对于艏垂线距离 | m | 38.7 |
| 重心距离船底基线高度 | m | 5.6 |
| 横摇惯性半径Rxx | m | 7.3 |
| 纵摇惯性半径Ryy | m | 22.6 |
| 艏摇惯性半径Rzz | m | 22.5 |
| 垂线间长 | m | 76 |
| 型宽 | m | 20.4 |
| 型深 | m | 8.0 |
计算网格包括五种,对应网格大小分别为1m、2m、3m、4m、5m。网格情况分别如图1.1~图1.5所示。计算模型和计算工况通过WARP进行处理,计算模型为仅考虑右舷的对称模型。计算周期为3~30s,间隔1s。计算角度为0~180°,间隔30°。水深100m。
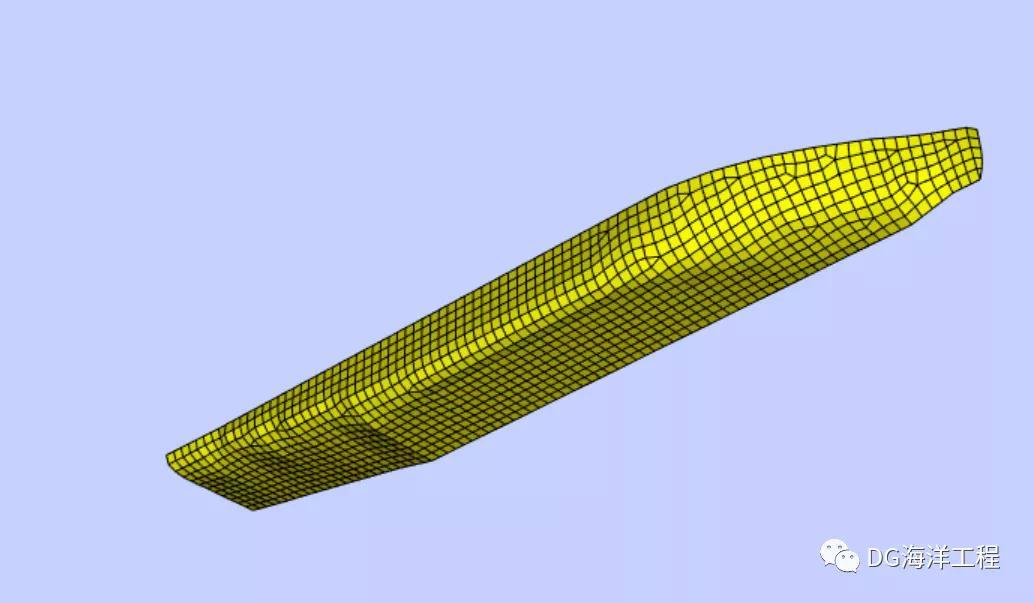
图1.1 MPV水动力计算网格--网格大小1m
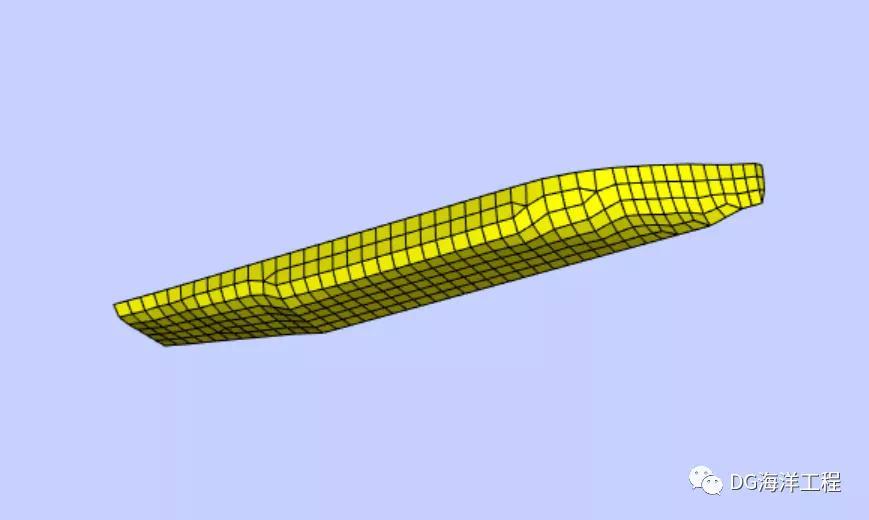
图1.2 MPV水动力计算网格--网格大小2m
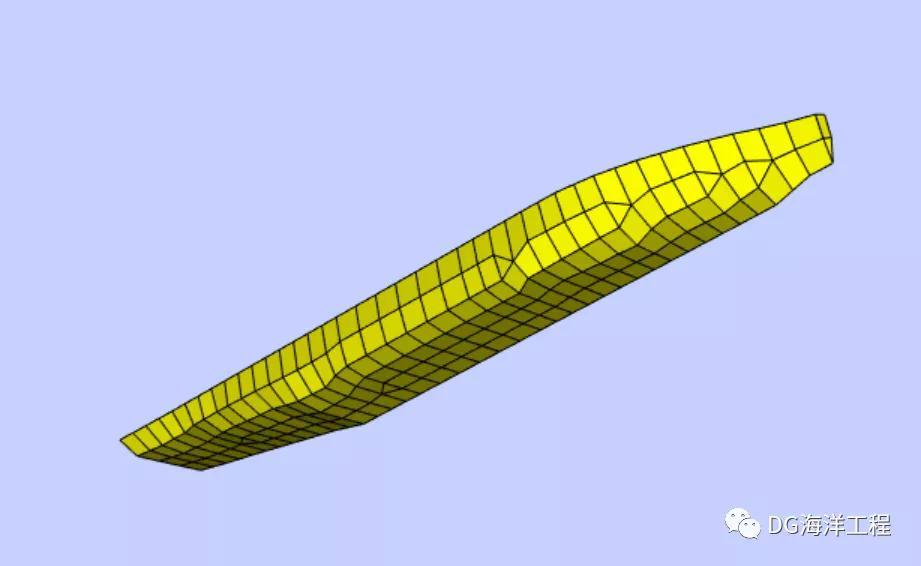
图1.3 MPV水动力计算网格--网格大小3m
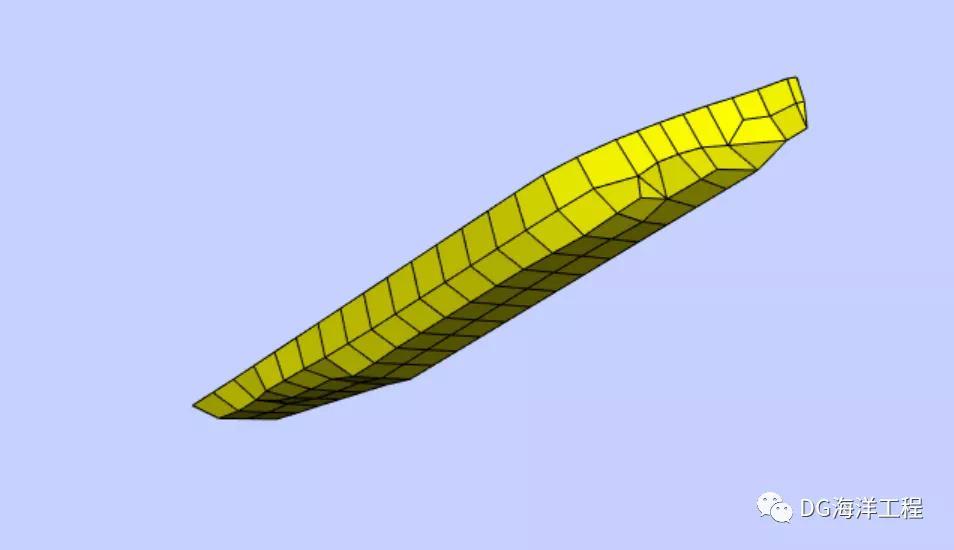
图1.4 MPV水动力计算网格--网格大小4m

图1.5 MPV水动力计算网格--网格大小5m
计算结果比较内容包括:
升沉、横摇、纵摇运动方向的附加质量与辐射阻尼;
90°浪向作用下的一阶升沉/横摇波浪载荷及其相位,0°浪向作用下的一阶纵摇波浪载荷及其相位;
Nemoh的计算结果与AQWA的结果对比。
1.1 不同网格计算的附加质量与辐射阻尼结果对比
图1.6~图1.11为不同网格模型给出的升沉、横摇、纵摇三个自由度的附加质量和辐射阻尼计算结对比。

图1.6 不同网格大小计算MPV升沉附加质量对比

图1.7 不同网格大小计算MPV升沉辐射阻尼对比

图1.8 不同网格大小计算MPV横摇附加质量对比

图1.9 不同网格大小计算MPV横摇辐射阻尼对比

图1.10不同网格大小计算MPV纵摇附加质量对比

图1.11 不同网格大小计算MPV纵辐射阻尼对比
对比结果显示,随着网格尺寸减小(船体网格越密),计算结果趋向收敛。随着周期的减小,大网格的计算精度下降,因而使用Nemoh在小周期范围内想要实现更高的计算精度需要更密的计算网格。
周期4s结果出现跳动,应为不规则频率。Nemoh不具备不规则频率去除功能,但网格的加密有利于降低不规则频率的结果震荡。
1.2 不同网格计算的一波浪载荷结果对比
图1.12~1.17为不同网格模型给出的升沉、横摇、纵摇三个自由度一阶波浪载荷及对应相位对比结果。

图1.12 不同网格大小计算MPV升沉一阶波浪力

图1.13不同网格大小计算MPV升沉一阶波浪力对应相位

图1.14 不同网格大小计算MPV横摇一阶波浪力

图1.15 不同网格大小计算MPV横摇一阶波浪力对应相位

图1.16 不同网格大小计算MPV纵摇一阶波浪力

图1.17 不同网格大小计算MPV纵摇一阶波浪力对应相位
对比结果显示,随着网格尺寸减小(船体网格越密),计算结果趋向收敛。较密的网格在小周期收敛性变好,但整体上一阶波浪力对于网格大小的敏感性弱于辐射载荷的结果。
1.3 Nemoh与AQWA的结果对比
这里对比Nemoh与AQWA计算的附加质量、辐射阻尼与一阶波浪载荷。AQWA与Nemoh的计算网格完全一致,均为1m大小。
为了保证条件一致,AQWA不去除不规则频率。
附加质量和辐射阻尼对比结果如图1.18~1.23所示。
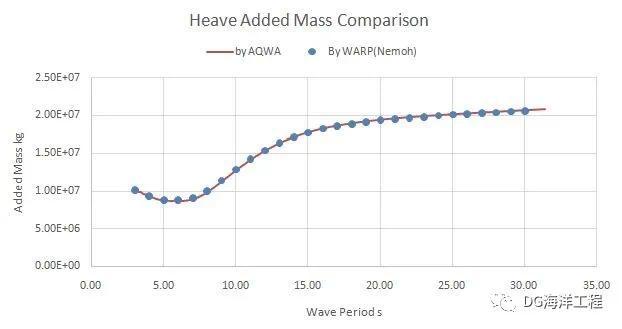
图1.18 升沉附加质量对比--Nemoh and AQWA

图1.19 升沉辐射阻尼对比--Nemoh and AQWA

图1.20 横摇附加质量对比--Nemoh and AQWA

图1.21 横摇辐射阻尼对比--Nemoh and AQWA

图1.22 纵摇附加质量对比--Nemoh and AQWA
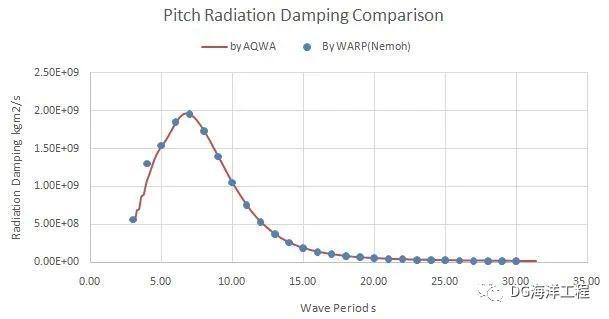
图1.23 纵摇辐射阻尼对比--Nemoh and AQWA
对比结果显示:同样的网格条件下,Nemoh计算的辐射结果与AQWA一致性较好,整体趋势一致,量级一致。AQWA在小周期(3~5s)曲线出现抖动,应是不规则频率的影响,Nemoh的计算周期并未与AQWA完全一致,因而并未体现出这一趋势。
图1.24~1.29为升沉、横摇、纵摇的一阶波浪载荷对比结果。

图1.24 升沉波浪力对比--Nemoh and AQWA

图1.25 升沉波浪力相位对比--Nemoh and AQWA

图1.26 横摇波浪力对比--Nemoh and AQWA

图1.27 横摇波浪力相位对比--Nemoh and AQWA

图1.28 纵摇波浪力对比--Nemoh and AQWA
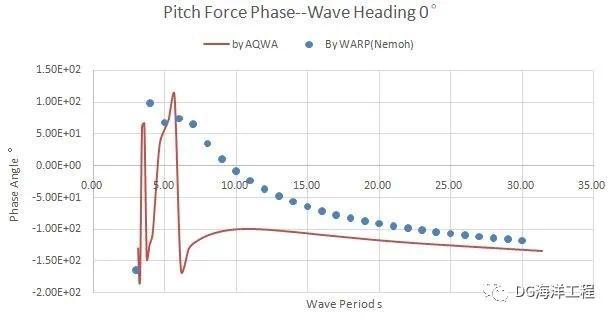
图1.29 纵摇波浪力相位对比--Nemoh and AQWA
对比结果显示:同样的网格条件下,Nemoh计��的波浪力结果与AQWA一致性较好,整体趋势一致,量级一致。Nemoh计算的纵摇载荷相位与AQWA不一致,目前尚未找到原因。
1.4 小结
本节对比了Nemoh不同网格大小对于计算结果的收敛性特征,计算结果显示:大网格在小周期范围内的计算精度较差,想要提高小周期范围内的水动力计算结果精度应使用整体网格更密的模型。
总体上,Nemoh一阶波浪载荷和辐射载荷的计算精度与AQWA差不多。
02
—
多体耦合计算精度对比
这里以 Goo.J 等[2]论文中对多体动力的研究作为参考进行耦合分析计算的结果对比,方驳与圆柱主尺度信息如下[1][2]:
| 项目 | 圆柱 | 方驳 |
| 长度 | \ | 109.7 |
| 宽度 | \ | 101.4 |
| 直径 | 95.8 | \ |
| 吃水 | 30 | 30 |
| 排水量 | 216200 | 333700 |
| 横摇回转半径 Rxx | 31.2 | 29.8 |
| 纵摇回转半径 Ryy | 31.2 | 30.4 |
| 艏摇回转半径 Rzz | 31.2 | 30.4 |
方驳位于圆柱右侧,波浪由方驳一侧向圆柱体传播,二者相距50m,水深100m。
对比同样网格和工况条件下Nemoh与AQWA的多体计算结果,计算模型如图2.1所示。

图2.1 方驳与圆柱体 by AQWA
方驳和圆柱在水动力耦合条件下的纵荡运动RAO如图2.2和2.3所示;方驳和圆柱在水动力耦合条件下的升沉运动RAO如图2.4和2.5所示。
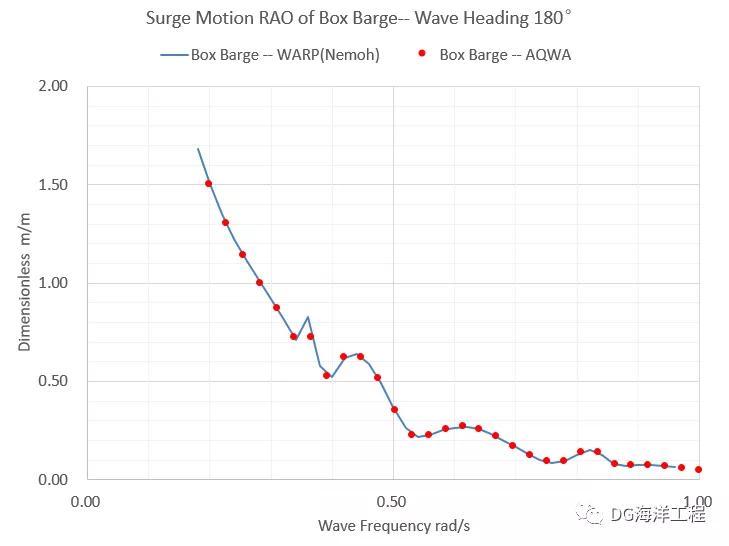
图2.2 水动力耦合条件下的方驳纵荡运动RAO

图2.3 水动力耦合条件下的圆柱体纵荡运动RAO
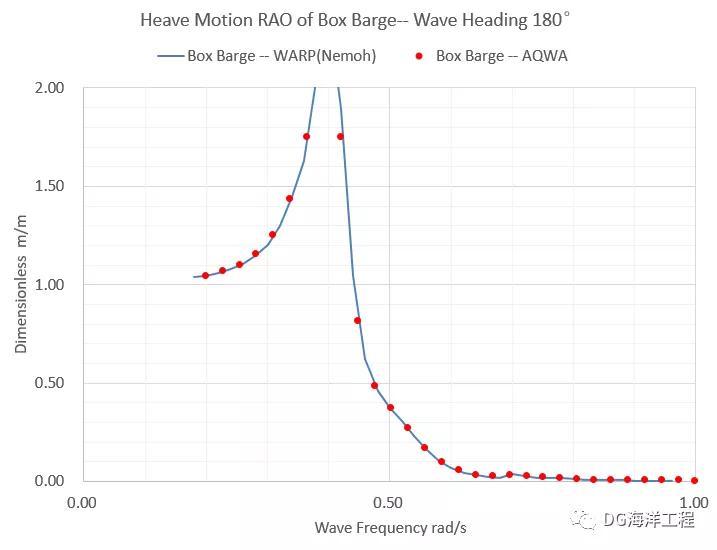
图2.4水动力耦合条件下的方驳升沉运动RAO

图2.5 水动力耦合条件下的圆柱体纵荡运动RAO
对比结果显示:同样的网格条件下,Nemoh多体耦合计算结果与AQWA计算结果高度一致,曲线走势与量级均一致。
这里给出计算结果与文献[2]结果的对比,如图2.6~2.9所示。对比结果显示Nemoh计算的两个体的纵荡运动RAO以及升沉运动RAO与文献结果趋势一致,量级一致,吻合情况良好。
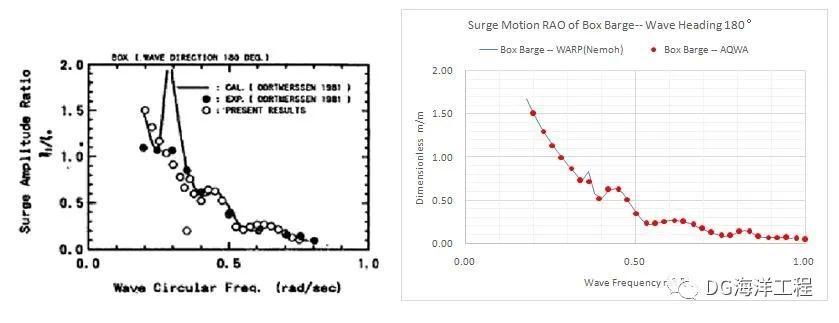
图2.6 水动力耦合条件下的方驳纵荡RAO文献结果对比

图2.7 水动力耦合条件下的圆柱体纵荡RAO文献结果对比

图2.8 水动力耦合条件下的方驳升沉RAO文献结果对比

图2.9 水动力耦合条件下的圆柱体升沉RAO文献结果对比
03
—
有月池结构物的计算精度对比
月池的存在对于基于三维辐射绕射水动力计算程序具有挑战,这里以解析解作为对比参考,比较同样模型和输入条件下有月池结构物的波浪力计算情况。

图3.1 计算模型俯视图
模型验证算例参数:
外径r=1+0.1cos(3θ)
内径r=0.5+0.1cos[3(θ+π)]
其中,θ为极坐标系下相对于x轴正方向的夹角,O0在全局坐标系中的位置为x=3m; y=4m,如图3.1所示
柱体总高度2 m; 一半浸没在水中,即吃水为1 m; 水深2 m
浪向30°
具体计算模型如图3.2所示。

图3.2 月池结构物
WAMIT计算结果与解析解对比结果如图3.3所示,横坐标为波数,力的单位进行了无量纲化。

图3.3 对于月池结构物波浪力的对比--WAMIT与解析解
对比结果显示,对于图3.2中的月池结构物,WAMIT的波浪力计算结果与解析解高度一致。
同样条件下Nemoh与WAMIT及解析解的对比结果如图3.4和3.5所示。

图3.4 对于月池结构物纵荡波浪力的对比--Nemoh、WAMIT与解析解

图3.5 对于月池结构物升沉波浪力的对比--Nemoh、WAMIT与解析解
对比结果显示,对于有月池结构物,Nemoh的计算精度不甚理想,纵荡波浪力计算结果趋势接近但有差异,升沉波浪力对于特征频率的捕捉存在差异。
04
—
小 结
本文对于三维辐射饶射水动力计算程序Nemoh的计算精度进行了部分验证,验证结果显示:
Nemoh对于水动力计算网格具有较大的依赖性,较密的网格对于小周期的问题求解有利;
Nemoh能够较好的解决常规的多体耦合水动力问题,更复杂的多体耦合计算精度还有待验证;
对于有月池的结构物,Nemoh的计算精度有限。
建议:
在使用Nemoh的时候需要严格遵循面元法对于网格的基本要求,提高计算精度;
使用Nemoh求解非常规水动力问题需要多加验证。





