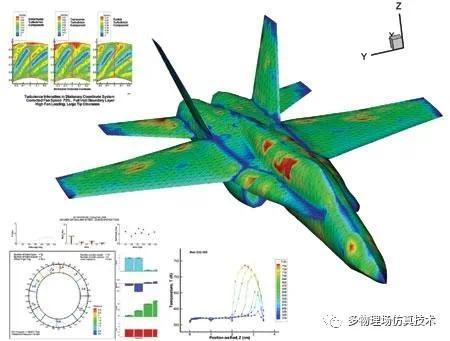
深入理解数值计算网格(1)--网格介绍

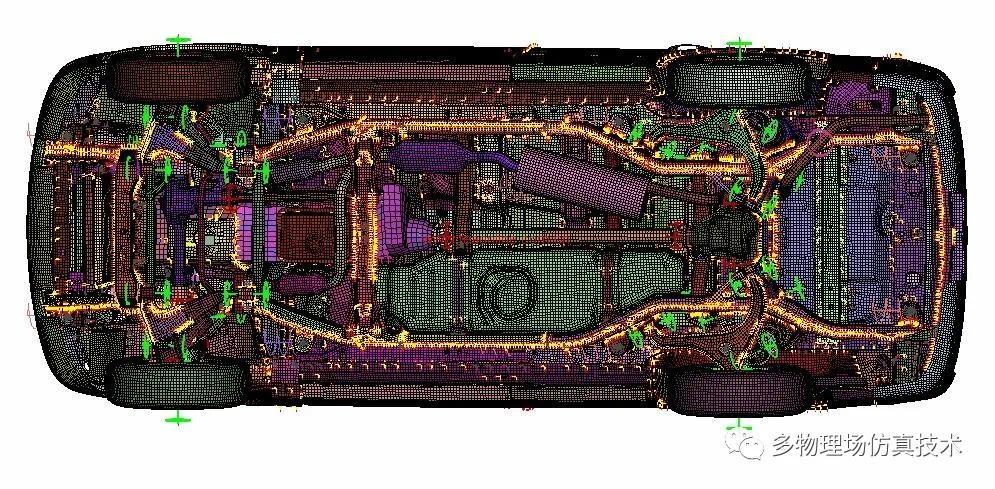
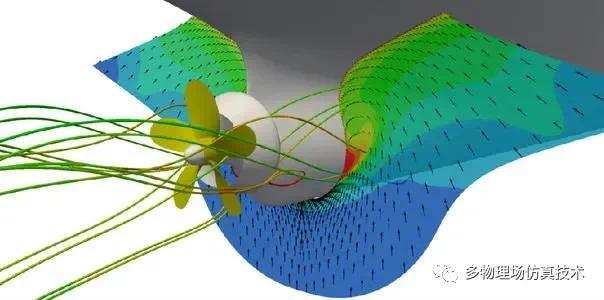
      以上图片均来源于网络，如有侵权，请与作者联系

网格(Mesh)在数值计算中有着举足轻重的作用。主流的数值仿真方法诸如有限元，有限体积，有限元，边界元都是以网格为计算对象。而差分法等，时域有限差分等也是以网格(Grid)点为计算对象。

什么是好网格？

网格的好坏直接决定了仿真计算能否成功，以及正确性，精度，性能。

简单的说就是尽可能用最少的网格，最真实的反应物理量的变化规律。

常见的网格种类：

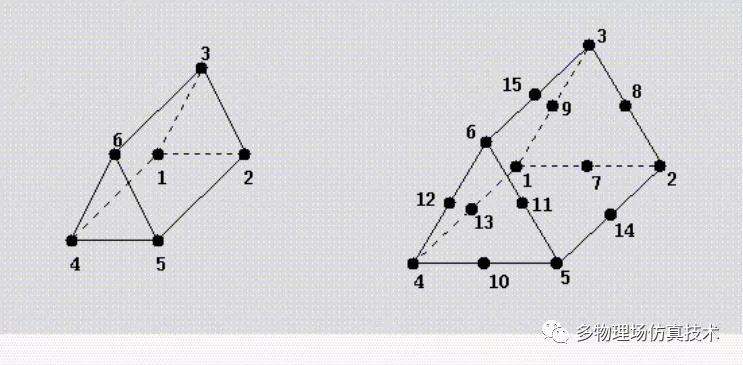
1. 三角形(Triangle)

以上图形从左往右分别为

左> 0阶一次单元，3个顶点，3条边

中> 1阶二次单元，6个顶点，3条边

右> 拉格朗日1阶二次单元，6个顶点，6条边

以下单元类型可以类推

2. 四边形(Quadrilateral)

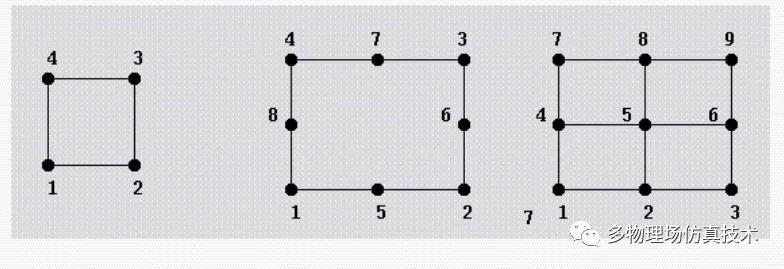
3. 四面体(Tetrahedron)

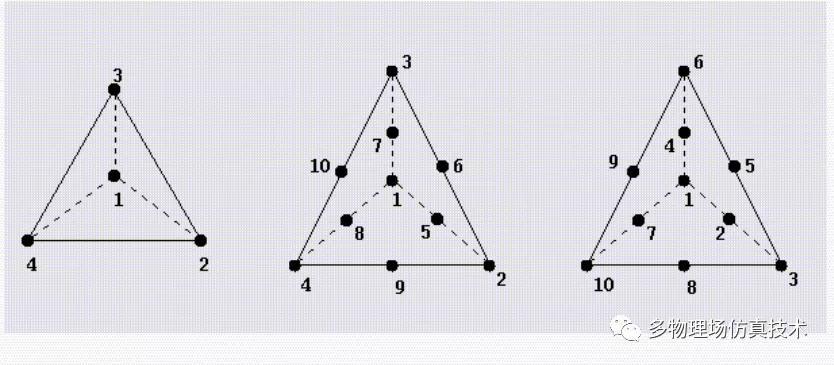
4. 六面体(Hexahedron)

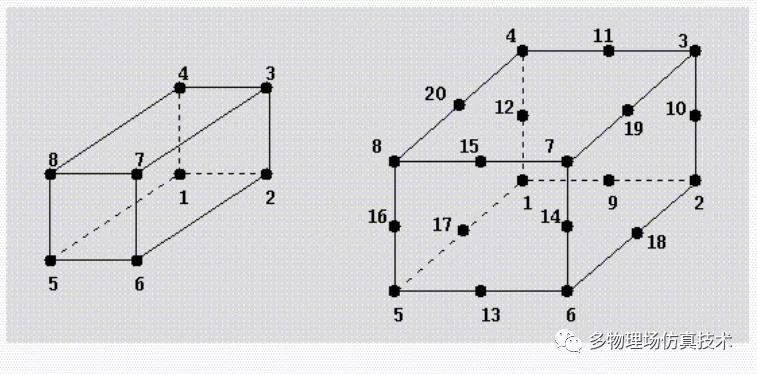
5. 金字塔单元(Pyramid)

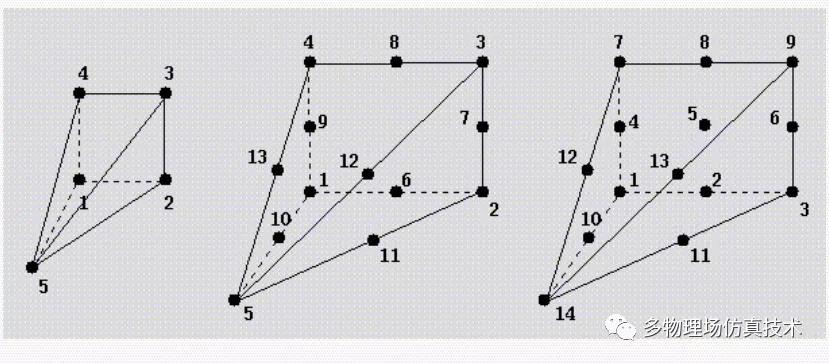
6. 楔形单元(Wdge)

网格的分类：

网格对应的英文有两个Mesh和Grid，Grid 的基本意思为格子，即四四方方非常规整的网格。

对于Mesh，我们通常分为结构化网格和非结构化网格。理解很简单，除了四边形和六面体是结构化网格，其它都是非结构化网格。

对于Grid，通常情况下我们用作有限差分方法的网格。

高阶单元：

除了上述我们提到的0阶1次单元以及1阶2次单元，在数值计算上还有更高阶的单元。高阶单元在数值计算上具有更高的精度，当然也会带来更大的计算量。在所有物理场的数值计算中，通常情况下1阶2次单元具有较好的性价比，即在精度和计算时间上有比较好的平衡。

以电磁矢量棱边3维四面体单元为例，其基函数自由度DOF与阶次的关系为：

DOF = (n 1)(n 3)(n 4)/2;    n为阶的数值

n=0时，DOF=6

n=1时，DOF=20

n=2时，DOF=45

n=5时，DOF=216

以电磁矢量棱边3维六面体单元为例，其基函数自由度DOF与阶次的关系为：

DOF = 3(n 1)(n 2)(n 2)

n=0时，DOF=12

n=1时，DOF=54

n=2时，DOF=144

n=5时，DOF=882

也就是说对于5阶的六面体单元，其一个单元的刚度矩阵可达882*882，对于开发验证，复杂度远远高于常用的0阶和1阶单元。

几何和网格

在网格之前，我们通常拿到的都是几何数据，比如BREP结构，STL面片结构，或者参数化的几何结构。

几何离散成的三角形称之为“面片”，非网格，大部分显示引擎底层都使用三角形来渲染对象，因此2维、3维几何都需要三角化（称之为“面片化”），比如一个长方体共有6个面，每个面需要离散成两个三角形，总共12个三角形。这12个三角形我们称之为12个“面片”，而非网格！一般情况下“面片”质量很差。“面片”有两个功能：一是用来做显示渲染数据；二是可以作为网格划分的输入数据，用来生成面网格。

对于隐式曲线曲面，需要设置合适的离散参数，从网格端进行解析。

有限元方法中的单元和网格

网格是几何上的概念，单元则是数值方法中的概念。

弹簧只能在一个方向上发生变形，是典型的1维单元；同理壳单元（shell）需要XY两个方向来定义，是2维单元；四面体，六面体是3维单元，也称为实体单元；对象可以看做质点的为0维单元，比如称之为“定楼神球"的调谐质量阻尼器。

网格生成算法

网格生成算法无论是在理论还是实际应用中都比较成熟，后续将会详细介绍。在这个领域很难有颠覆式的发展，未来网格底层生成算法可以和实际工业应用更加紧密结合，优化网格生成效率。