任意拉格朗日-欧拉方法(ALE)处理流固耦合问题
1. 引言
有限元法 (FEM) 和任意拉格朗日-欧拉 (ALE,Arbitrary Lagrangian-Eulerian) 方法都是计算流体动力学和结构力学中使用的数值技术。FEM是一种用于寻找偏微分方程边值问题近似解的数值技术,它将一个大系统细分为更小、更简单的部分,称为有限元,然后将这些有限元的简单方程组装成一个更大的方程组来模拟整个问题。FEM 使用变分方法,通过最小化相关误差函数来求近似解。
ALE是一种用于解决涉及移动边界的计算方法,它使用混合描述,结合了跟踪单个流体粒子的拉格朗日描述和关注空间中 特定位置的欧拉描述。ALE 方法在网格需要移动以适应材料形状变化(例如流体-结构相互作用)的模拟中 特别有用,该方法的灵感来自数学家欧拉和拉格朗日对连续介质力学的单独描述。
FEM 和 ALE 之间的主要区别在于它们处理变形的方式:在 FEM 中,网格随材料移动(拉格朗日方法),如果变形很大,可能会导致单元高度扭曲。在 ALE 中,网格可以独立于材料移动,这可以防止发生大变形时发生单元变形。
许多商业性软件内置了ALE方法,例如COMSOL, Adina和Abaqus。此外,材料点法(例如Anura3D)也使用了ALE技术。值得一提的是,FLAC3D正在考虑合并ALE技术来处理岩土工程的大变形问题。
2. COMSOL中的ALE
下面的几何模型是一个水平的流道,在流道中间设立一个窄的垂直结构作为障碍物,流体从左边界进入向右流动,障碍物的出现使得流体进入通道上半部分的窄道,流体对结构
施加了由粘性阻力和流体压力产生的作用力。结构由可变形材料组成,在流体力的作用下发生了弯曲,导致流体也会沿着新的路径流动。这个模型如果在原始几何中求解会导致不合理的模拟结果。
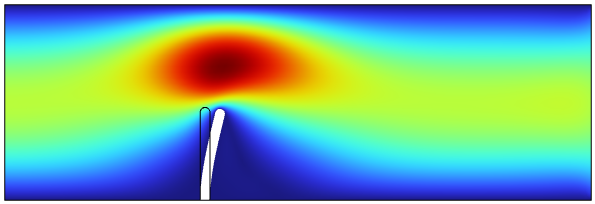
COMSOL Multiphysics 流固耦合 (FSI) 多物理场接口将流体流动与固体力学相结合,以捕获流体与固体结构之间的相互作用。固体力学接口和单相流接口分别模拟固体和流体,FSI 耦合出现在流体和固体之间的边界上。
COMSOL使用ALE方法处理流固耦合,通过动网格来处理几何的变形和边界的移动,将使用欧拉描述和空间框架制定的流体流动与使用拉格朗日描述和材料框架制定的固体力学相结合,ALE 方法处理变形几何体的动力学以及使用移动网格的移动边界,基于结构的移动边界和网格平滑处理来计算通道区域的新网格坐标,根据结构边界的移动和网格平滑计算通道区域上的新网格坐标,在移动坐标系中求解流动的纳维-斯托克斯(Navier-Stokes)方程。
模型的结构力学部分不需要使用 ALE 方法, COMSOL按照常规方法在固定坐标系中对其求解。但是,ALE 方法需要基于结构力学分析得出的应变结果来计算新网格的坐标。
3. 移动网格
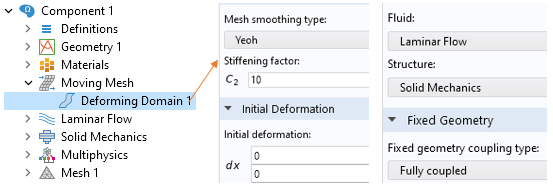
ALE的核心设置是移动网格(Moving Mesh),需要选择网格平滑类型(Mesh smoothing type)。平滑类型有四种:Laplace、Winslow、Hyperelastic 或 Yeoh(默认)。对于 Yeoh,还需要输入刚性系数(Stiffening factor)C2 (默认值10)。在初始变形字段中输入初始变形分量的表达式或值(m)。
Laplace平滑在计算方面是最便宜的选择,因为它是线性的,对每个坐标方向使用一个方程,并且彼此不耦合。然而,Laplace平滑中没有机制可以防止单元反转。因此该方法最适合线性区域中的小变形,例如计算某些量对初始形状周围虚拟变形的敏感性。
Winslow、Hyperelastic 和 Yeoh 平滑方法越来越非线性,并为所有坐标方向创建单个耦合方程组,这使得求解它们的成本更高。它们还具有共同的理论特性,即这些方程的连续解在任何地方都始终具有正体积。不幸的是,对于离散有限元解来说不一定如此。此外,正体积不足以维持单元质量。
在压缩中,三种非线性方法表现出相似的行为,而在拉伸中,Winslow平滑往往允许单元拉伸得太远。更简单的Hyperelastic方法和更先进的 Yeoh 模型之间的主要区别在于,后者通过急剧增加扭曲单元的刚度来响应单元扭曲,这在某种程度上防止了这些区域的进一步变形,并有效地将网格变形更均匀地分布在域上,远离移动边界。
Yeoh 平滑通常会产生最佳结果,并在网格单元反转之前允许最大的边界位移。然而,由于其很强的非线性,它可能会导致收敛问题,特别是对于瞬态和分离求解器。




