VirtualFlow │ 输油管气液两相分层流演化及段塞形成的大尺度三维模拟
液-液流动出现在各种工业过程中,特别是在石油工业中,气体与伴生液体(油、凝析油和/或水)的混合物一起生产和运输。当可变形界面在管道中共流时,它们获得了flow regimes/flow patterns的各种特征分布。理解从分层流到段塞流的转变在油气输送系统中是很重要的,因此其不断地推动着这一方向的研究。段塞流是水平和近水平气液流动中常见的一种流型,其处于大相干扰动状态,从而引起大的压力波动和流量变化,将影响工艺设备。其另一个特点是间歇出现充气液体团块,这些液体团块完全填满了管道的横截面,并以很大的速度向下游流动。
本文通过两类CMFD方法:CFX软件的双流体模型与VirtualFlow的Level Set方法进行数值模拟以解决段塞流形成的问题。首先比较两种预测二维管道中分层流动的方法,随后在只使用Level Set方法的计算结果讨论了在湍流条件下圆形三维管道中分层流向段塞流过渡的结果。湍流通过由Liovic和Lakehal(2007)扩展到界面两相流的LES方法来建模,即自由界面大涡模拟(LEIS)。
模型描述
界面跟踪vs.双流体概念
界面流动是指两种或两种以上的不混相流体被随时间变化的尖锐界面所分离的多相流动问题。通常,当界面一侧的流体是在界面上施加切向应力的气体时,则该界面则被称为自由表面。ITM方法最适合对这类流动进行处理,因为其相当准确地表示了接口拓扑。当界面的确切形状无法确定或相关性较弱时,可借助双流体方法,其中每个相需要单独的守恒方程,并考虑两相之间的作用力。这两类方法都可处理界面流,但精度不同。ITM是本文介绍的单流体方法的基础算法。
单流体方法需要求解一组具有可变材料性质和表面力的守恒方程(Lakehal等 2002)。因此,该方法比双流体模型更准确,因为它最大限度地减少了建模假设。在单流体形式中表示的不可压缩多相流动方程采用以下形式:

其中ρ是密度,p是压力,μ是粘度,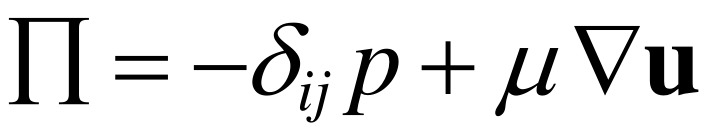 。方程(2)中最后的一项表示表面张力,n表示到界面的法向量,κ为表面曲率,γ为表面张力系数,δ表示以界面为中心的光滑狄拉克函数。在这里采用的Level Set方法(Sussman et al 1994)中,互不掺混流体之间的界面用连续函数φ表示,φ表示到界面的距离,在界面上设置为零,在一侧为正,在另一侧为负。材料属性、体力和表面力作为此函数的函数在局部更新,并使用平滑的Heaviside函数在界面上进行平滑:
。方程(2)中最后的一项表示表面张力,n表示到界面的法向量,κ为表面曲率,γ为表面张力系数,δ表示以界面为中心的光滑狄拉克函数。在这里采用的Level Set方法(Sussman et al 1994)中,互不掺混流体之间的界面用连续函数φ表示,φ表示到界面的距离,在界面上设置为零,在一侧为正,在另一侧为负。材料属性、体力和表面力作为此函数的函数在局部更新,并使用平滑的Heaviside函数在界面上进行平滑:
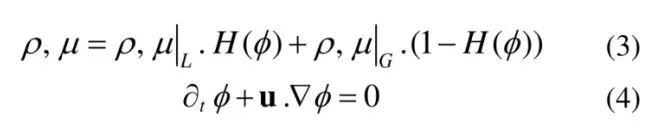
在实践中,Level Set函数在方程(4)的单步迭代后不再是距离界面的带符号距离。为了恢复其在界面附近的正确分布,使用三阶或五阶WENO格式将re-distancing方程迭代到稳态。
不可压缩流动条件下不存在相变时,k相层流运动方程用平均双流体形式表示为:

式中 是表观密度,
是表观密度, 为孔隙率
为孔隙率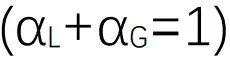 ,实际上为当地的气液体积比。假定系统压力唯一,通过界面交换力对每个相交替进行耦合求解。
,实际上为当地的气液体积比。假定系统压力唯一,通过界面交换力对每个相交替进行耦合求解。
需要类似于(4)的拓扑方程来更新空隙率随时间的变化,但不能与ITM的(例如Level Set和VOF)进行相似。方程(6)的RHS项反映了动量方程中相间相互作用力,即 。例如在散体流动中,RHS项将包括增加的质量、曳力、升力(以及固体颗粒的萨弗曼力)。对于自由表面流动,该项包括基于滑移速度定义的界面剪切力
。例如在散体流动中,RHS项将包括增加的质量、曳力、升力(以及固体颗粒的萨弗曼力)。对于自由表面流动,该项包括基于滑移速度定义的界面剪切力 。与前面提出的单流体方法相比,这个方程的问题在于需要确定特定系数(例如
。与前面提出的单流体方法相比,这个方程的问题在于需要确定特定系数(例如 )来确定动量交换项。
)来确定动量交换项。
二维段塞流的形成
在二维平面管道中模拟二维段塞流动的形成过程,两相流体是液态和气态氨,与参考对比的实验工况相同(Martin等, 2005)。计算域为一根长6.3m,内径146.3mm,壁厚11mm的碳钢管。管道两端关闭,但在管道顶部设置有两个直径0.3m的孔是开放的,分别设置为入口和出口,流体从这两个孔进入和离开管道。纯氨最初被放置在隔热的水平管道中,在指定深度达到热平衡,初始深度从38.1mm到127mm不等。在顶部入口处,流速在1-10m/s之间变化。使用的计算网格由400×20个节点组成。两侧壁面采用无滑移边界条件,在管道的右端出口处采用outflow边界条件。
Level Sets(LS)结果

图1:段塞流形成VL,0=5 m/s (Level Sets)
图1展示了管道流动中波浪的发展情况。入口流速为5m/s,气液交界面选择空隙率为50%。该图显示了在经过不同时间步后,数值计算得到的自由表面变化情况。段塞的形成过程清楚地表明是一阶模态生长的结果。结果显示其是由压力造成的,而非由施加的剪切造成。在第一模态(高振幅长波)的尾迹中形成的第二模态(短波),其在第4幅图中与一阶模态合并导致管道密封。图1展示的结果很好地说明了这种模态间的相互作用或波-波间的相互作用过程。
段塞流在距离入口6个通道高度的下游形成(第5幅图)。随着时间的推移,液体形成的堵塞会导致更多的液体积聚(最后3幅图),这似乎进一步隔离了气体段塞。该阻塞机制不断重复,最终沿着管道形成连续的段塞。第5幅图中显示出两种新模式的生长,这随后引起波的合并,产生第二个阻塞,段塞最终在管道的右端消散。
双流体模型结果
图2是在入流速度为5m/s工况下,采用双流体模型得到的自由液面演化过程。波生长机制的开始方式与Level Set模拟的结果非常相似。但与Level Set方法的模拟结果相反,在第一幅图上已经出现了各种其他的模式,在较远的下游处的自由表面开始出现表面的不稳定现象。这是因为在Level Set模型中,表面张力阻止了短波的形成,而在双流体模型中,表面张力无法平衡界面剪切的作用。

图2:段塞流形成VL,0=5 m/s (2-fluid)
双流体模型本质上并不能预测尖锐界面。段塞在接近管道的右侧时出现消散,如图2的最后3幅图所示。在这种情况下,并没有观察到LevelSet模拟得到的流动结构。相反,这两种液体倾向于逐渐混合均匀。图2中的绿色等高线反映了双流体模型计算结果中混合带的存在。这是双流体方法与ITM方法相比的另一个缺点,ITM方法现在被证明是最适合这类流动的。当双流体模型应用于自由表面流动时,另一个误差来源是缺少一个严格的界面阻力模型 。
。
三维圆管段塞流的形成
问题建立
建立一个完整的三维计算域。部分网格如图3所示。管道长6.3m,管径0.14m。采用多块网格策略,用相邻子域覆盖域,处理器12个,MPI并行执行,网格数量近36万。采用引言中提到的One-Fluid-LES方法(LEIS方法)。具体来说,其利用Level Set技术进行界面跟踪。湍流采用由Liovic和Lakehal(2007)扩展到界面两相流的LES方法建模。
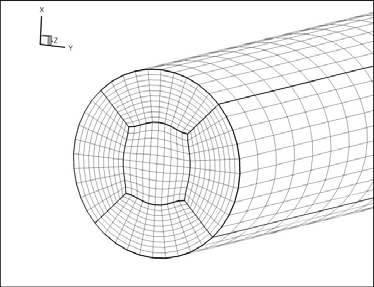
图3:使用BFC生成的多块计算网格
流入边界条件包括固定的表面气液速度和空隙率,条件与Martin等(2005)的实验保持相同,管道右端保持敞开。入口处设置气体速度为14m/s,液体速度为0.5m/s,气液以入口中线为界。入口流入的液体温度为-33℃,气体温度为20℃。基于壁面剪切雷诺数,在整个流域内施加初始流动扰动。
整体水动力学特征
下图为进口气体速度为14m/s,空隙率为50%的气液管道流动中波浪的发展情况。图4显示了在不同时间步后自由液面的位置变化情况。在压力和界面剪切作用下,在距离入口约1.5倍管径处形成一阶波模态,波面具有三维特征。较小的斜坡波在下游进一步发展。二阶波模态在一阶波模态之后形成。在段塞形成前,二阶波试图进一步向下游的一阶波合并。段塞流在距离入口6倍管径的下游形成。与上文中的二维模拟的不同之处在于,密封前形成的短、低振幅波本质上是三维的,自由液面沿展向分布存在不均匀的特征。
值得注意的是,在段塞的下游,由于液面与气体之间发生剪切,以及湍流结构的强烈相互作用,形成了各种坡度和波长的自由液面变化。此外,密封前形成的初始波型呈侧向倾斜,并非完整的正弦波形。图4中最后一幅图显示波峰在密封时的不稳定性,导致强烈的表面起皱,正如Liovic和Lakehal(2007)在破碎波中发现的那样。



图4:不同时刻的自由液面位置变化
随着时间的推移,由液体形成的堵塞会导致更多的液体积聚,这进一步隔离了气体段塞。该机制不断重复,最终沿着管道形成连续的段塞。
表面湍流相互作用
图5展示自由表面以及速度在x,y,z三个方向上的分量大小(云图颜色),分别显示在二维中心y-z平面上。图5显示在液体发生密封后,流场中立即形成的旋涡并脱落。三个方向上的瞬时速度分量证实了这一点,尤其是沿流向(z方向)的速度表现最为明显。








图7:正、负涡度等值线(ωx,ωz)
图6展示了段塞密封后自由表面的破裂过程,图中结合展示自由表面和速度等值线。图6的第3幅图展示了破碎过程对分层液体自由液面的影响,该区域具有非常高的湍流强度。
图7展示了正和负涡度水平的情况,结果表明,即使在段塞破裂之前,湍流在段塞的下游也特别活跃。在波舌的撞击处产生的湍流非常高,最终会穿透到表面之下。这些流动结构以及湍流的产生和传输与破碎波中揭示的规律非常相似(Liovic & Lakehal, 2007)。
段塞速度
图8讨论了段塞尾部和中心的位置随时间的变化,显示了段塞位置与时间的关系,并揭示了二者对时间的线性依赖关系,这与Martin等人(2005)的测量结果一致,他们在该工作中再现的相同流动条件下获得了平均段塞流速度Us=9.4m/s。在该工况下,段塞速度保持恒定,与上文中二维模拟的结果相同。对于水动力学中的段塞流动,如果管道中含气率已知,可根据气液流速计算段塞流速度。在水平线上,段塞流内液体的平均速度近似等于混合速度,或者也可以用解析法估计(Collins et al, 1978):

其中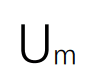 代表混合速度。图8结果表明,LES模拟预测的段塞速度(尾部和中心)与理论解一致,给出的
代表混合速度。图8结果表明,LES模拟预测的段塞速度(尾部和中心)与理论解一致,给出的 =9.33 m/s,与Martin等人的实验(
=9.33 m/s,与Martin等人的实验( =9.4 m/s)一致。
=9.4 m/s)一致。

图8:段塞位移随时间和速度的变化
对于工程实际应用而言,计算结果表明,即便在使用粗网格的条件下,LES方法依旧能够预测管道流动的重要流动特征。而更精细的网格将有助于获得段塞流在流动自由表面上俯冲后的流动和两相分布的详细图像。

图9:过渡到段塞流标准:CFD vs.理论
段塞的起源:与理论解比较
Wallis和Dobson(1973)、Taitel和Dukler(1976)以及其他很多前人的研究已经形成了从分层流动到段塞流过渡的阈值标准。这里将本文CFD结果与Taitel和Dukler(1976)的理论进行对比,该理论解认为段塞流形成的阈值依赖于无量纲体积气体通量和空隙率(α=AG/A):

式中,AG为气体所占面积,D为管道直径,g为重力,A为管道横流面积,M为质量通量。Taitel和Dukler(1976)的模型也与Martin等人(2005)提出的模型进行了比较,基于他们的测量,根据JG*=1.4α2将发生段塞的临界体积通量与空隙率联系起来。图9中展示的CFD结果与理论解之间的对比包括二维层流与三维湍流的结果。
从二维结果来看,绿线对应的气体名义速度为5m/s,确实可以预测段塞流的形成,尽管该值略低于Taitel & Dukler模型的阈值。双流体模型的二维结果不包括在内,因为与ITM的模拟相比,很难从图像上定义双流体模型结果中的段塞流判断。三维模拟结果表明,阈值与Martin等人的模型相当吻合,这实际上远远高于Taitel & Dukler的模型。
结论
本文研究气液二维通道和三维管道流动中波浪的发展与入口空隙率和气体雷诺数的关系。CFD结果基于VirtualFlow计算流体力学软件,使用Level Set方法进行模拟。结果表明,该方法在段塞流动预报方面优于双流体方法。双流体方法将会导致气液界面模糊,在密封区下游产生非物理的混合流区。VirtualFlow对三维湍流的模拟提供了更好的流动细节图像,特别是关于段塞形成和湍流界面相互作用的开始,同时对段塞区速度的预测进行了实验和理论对比验证。
从工程应用角度来看,基于VirtualFlow的数值计算结果在管道石油运输领域与使用一维集总参数模型相比可以更严格地接近真实解。数值结果证明,基于VirtualFlow可以使用相同的方法处理复杂地形上的管道多相流动包括含固体颗粒(散体)的复杂多相流动过程。实践表明,如果对1.6km长的管道进行数值仿真,网格量约在500万左右,预计将需要在32个CPU的Linux集群上进行1周的数值计算。




