如何选择加窗函数?
在我们进行信号分析时候,一般会截取有限长度的信号波形做傅里叶变换,如果这个信号不是周期信号,这个截断过程会产生泄漏,即使是周期性信号,截断的长度不是周期的整数倍,这个阶段的信号也会存在频谱泄漏,导致功率扩散到整个频谱范围,产生大量“雾霾数据”,无法得到正确的频谱结果。虽然知道加窗可以抑制泄漏,但复杂的窗函数表达式及抽象的主瓣旁瓣描述方法,令人更加迷惑,下面我们抛弃公式用通俗易懂的方式介绍窗函数的选择。
加窗与窗函数
我们在之前文章EMI接收机对信号做傅里叶变换中时间窗与RBW的关系里提到,常见的时间窗类型包括:Rectangular、Hamming、Hanning、Gaussian,Blackman、Kaiser、Flat-Top等。
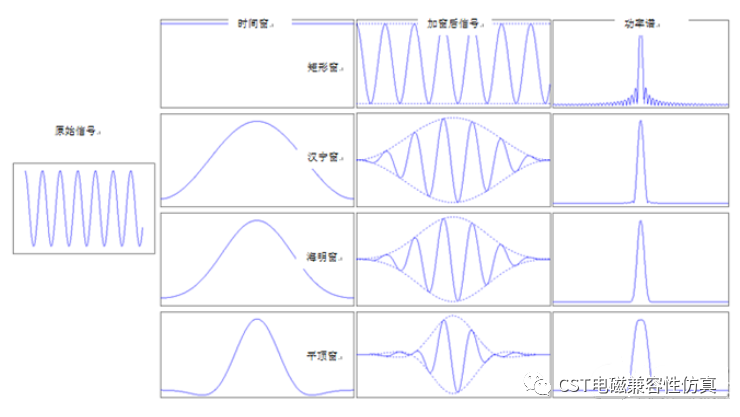
如图直观地描述了四种信号加窗的过程及窗函数基本特征。在时域上看,加窗其实就是将窗函数作为调制波,需要加窗的信号作为载波进行振幅调制(简称调幅)。矩形窗相当于对输入信号乘以1,对截取的时间窗内的波形未做任何改变,而其它三种窗函数都将时间窗内开始和结束处的信号调制到了零。
更普遍地,绝大部分窗函数形状都具有类似从中间到两边逐渐下降的形状,只是下降的速度等细节上有所区别。这个特征体现了加窗的目的——降低截断引起的泄漏,所有窗函数都是通过降低起始和结束处的信号幅度,来减小截断边沿处信号突变产生的额外频谱。
我们来看一下几种窗函数的频谱特点:
(1)矩形窗
矩形窗主瓣较窄,第一旁瓣峰值-13dB,旁瓣衰减速度20dB/十倍频,通带衰减大,阻带衰减小,导致变换中容易带进高频干扰和泄露。

(2)海明窗
海明窗也是余弦窗的一种,又称改进的升余弦窗。海明窗与汉宁窗都是余弦窗,只是加权系数不同。海明窗加权的系数能使旁瓣达到更小。分析表明,海明窗的第一旁瓣衰减为-42dB.海明窗的频谱也是由3个矩形时窗的频谱合成,但其旁瓣衰减速度为20dB/十倍频,这比汉宁窗衰减速度慢。
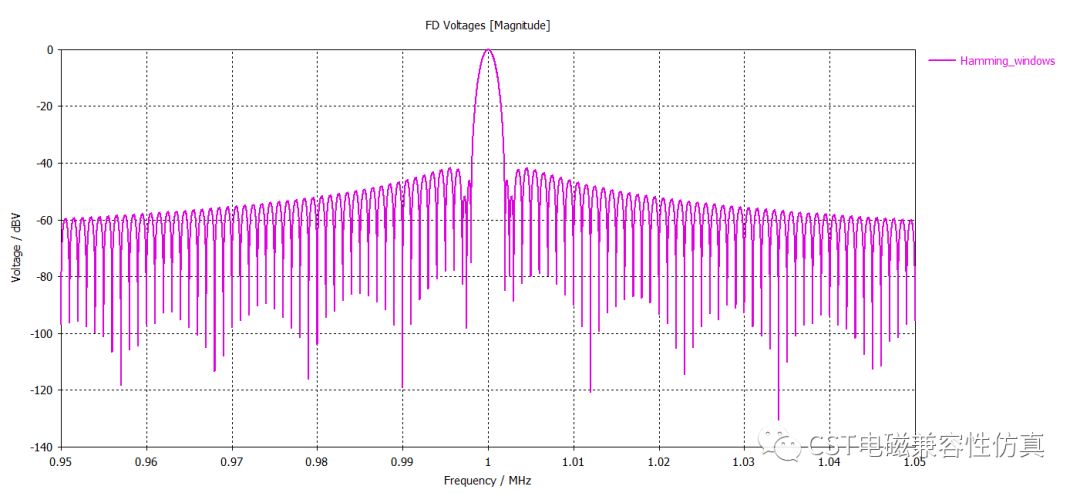
(3)汉宁窗
汉宁窗,即一种余弦窗,主瓣较宽,第一旁瓣-32dB,旁瓣衰减速度60dB/十倍频。
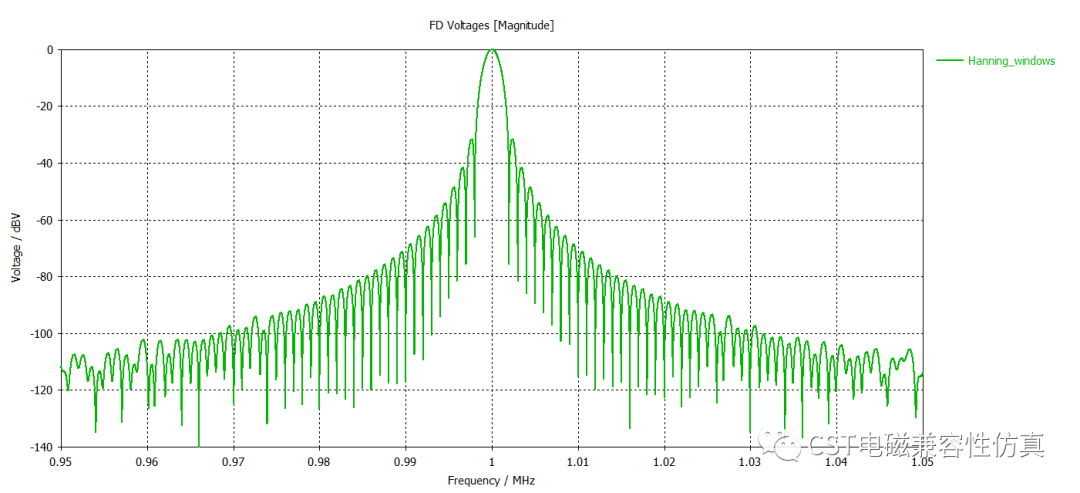
(4)高斯窗
高斯窗,即一种指数窗,高斯窗谱无负的旁瓣,旁瓣没有波动较为平坦。高斯窗谱的主瓣较宽,故而频率分辨力低,非常适用于截取非周期性信号。
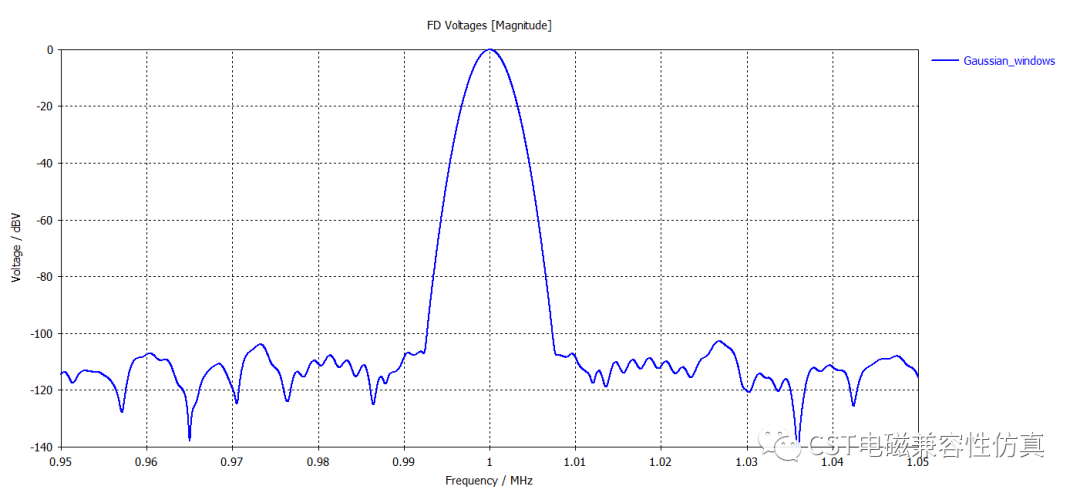
(5)布莱克曼窗
布莱克曼窗是一种类似于汉明窗与汉宁窗的窗函数,号称最平坦旁瓣,主瓣宽,旁瓣小,频率识别精度最低,但幅值识别精度最高。
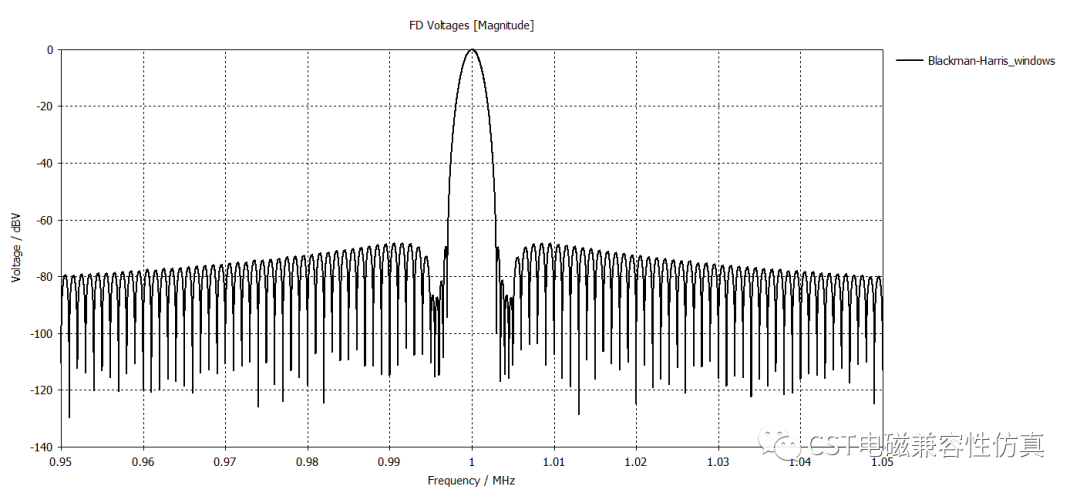
(6)Kaiser窗
Kaiser窗是一种最优化窗,它的优化准则是:对于有限的信号能量,要求确定一个有限时宽的信号波形,它使得频宽内的能量为最大。
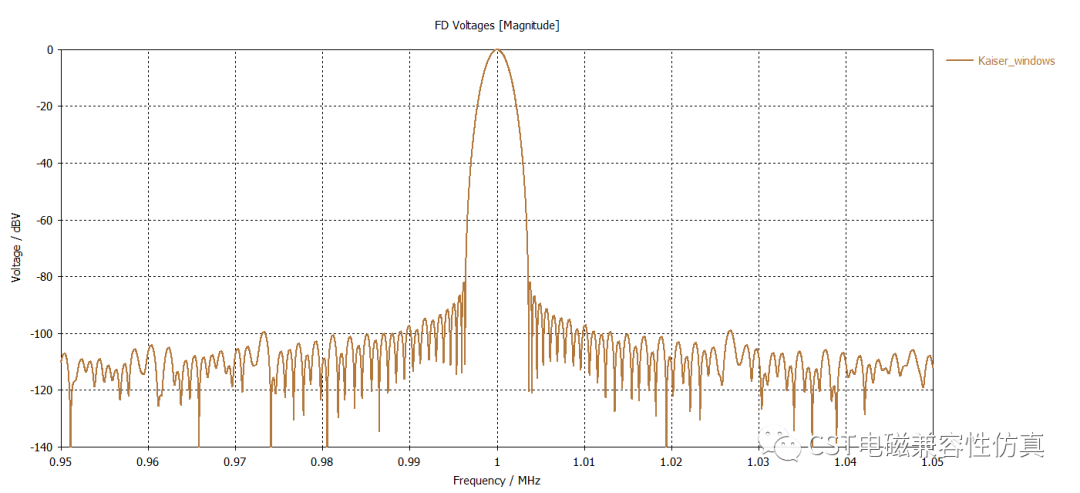
(7)平顶窗
平顶窗主瓣稍宽,幅度的准确性更高,第一旁瓣-93.6dB
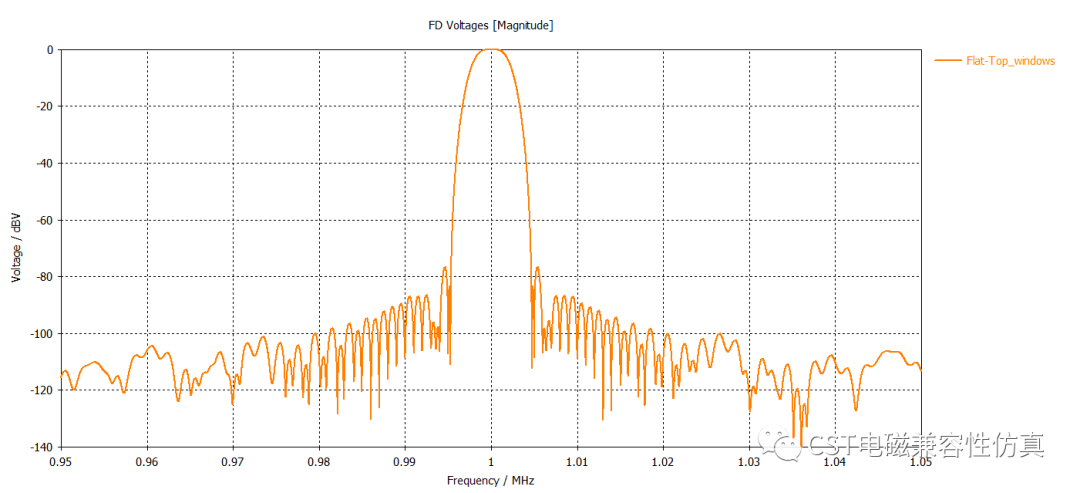
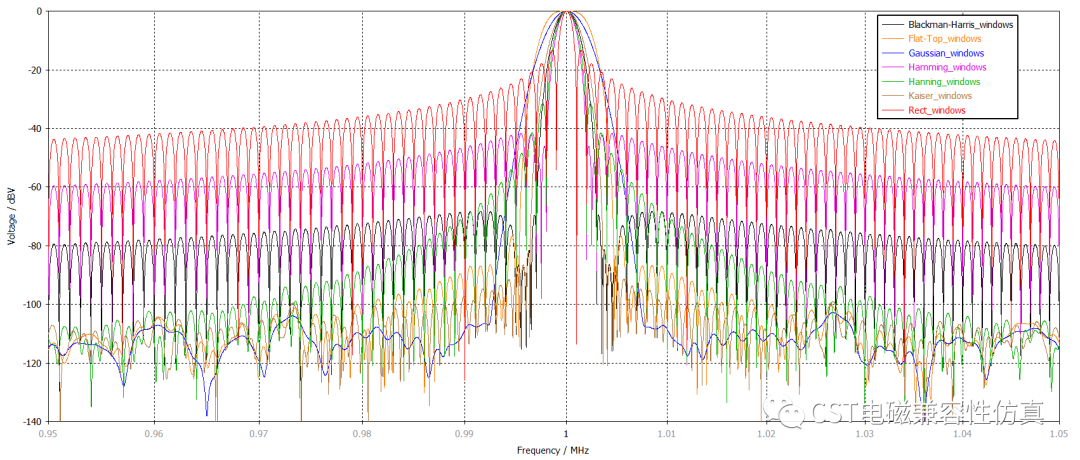
最后我们来看一下七个窗函数的对比:
如何选择加窗函数?
加窗后信号时域的变化显著,由于后续的信号处理一般都是进行傅里叶变换,所以我们主要分析加窗对傅里叶变换结果的影响。傅里叶变换后主要的特征有频率、幅值和相位,而加窗对相位的影响是线性的,所以一般不用考虑,下面讨论对频率和幅值的影响。
加窗对频率和幅值的影响是关联的,对于时域的单个频率信号,加窗之后的频谱就是将窗谱的谱峰位置平移到信号的频率处,然后进行垂直缩放。说明加窗的影响取决于窗的功率谱。
再来看窗函数的功率谱,从上到下,窗函数的主峰(即主瓣)越来越粗,两边的副峰(即旁瓣)越来越少,平顶窗的名称也因主瓣顶峰较平而得名。主瓣宽就可能与附近的频率的谱相叠加,意味着更难找到叠加后功率谱中最大的频率点,即降低了频率分辨率,较难定位中心频率。旁瓣多意味着信号功率泄漏多,主瓣被削弱了,即幅值精度降低了。
有了规律,窗函数的选择就简单多了。
(1)在需要频率分辨率高时,使用旁瓣少的窗口,如汉宁窗,而矩形窗旁瓣太多,泄漏太大,无法抑制泄漏。
(2)在需要幅值准确时,可以使用平顶窗。
(3)对于一次过程时间小于窗口的暂态信号或冲击波形,信号开始和结束处本身就是零,不存在截断引起的泄漏,不需要加窗抑制,因此只需要用矩形窗即可。
(4)对于处理非周期性信号,而且频谱不需要旁瓣分辨率高,旁瓣较少,并且对高频干扰和泄漏要求较高,需要用到高斯窗和凯瑟窗。
(5)对于连续的周期性波形,可以结合不同的窗口获得所关注的结果。


