Johnson-cook 本构模型 umat子程序
Johnson-Cook 材料模型及失效模型。一般用于描述大应变(large strains)、高应变率(high strain rates)、高温(high temperatures)环境下金属材料的强度极限以及失效过程。在Johnson-Cook强度模型中,屈服应力(yield stress)由应变、应变率以及温度决定。
屈服应力的表达式为:
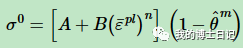
其中,A,B,N,M是材料参数,epsilon_pl是等效塑性应变,θ_m是无量纲的温度,定义为:
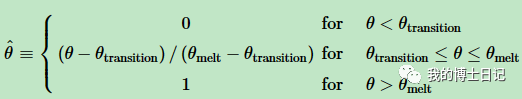
其中θ是当前温度,θ_melt是材料的熔融温度,θ_transition是转变温度,定义为屈服应力不依赖于温度的转变温度。材料参数A、B和n必须在转变温度或低于转变温度时测量。材料参数m应基于高于转变温度的测量值来确定,如果指定零值或未指定m值,则忽略σ0的温度相关性,当θ≥θ_melt时,材料将熔化,并表现为流体;由于σ0=0,因此不会有剪切阻力。通过将等效塑性应变设置为零,将消除硬化记忆。如果为模型指定了背应力,这些背应力也将设置为零。如果在材料定义中包含退火行为,并且退火温度定义为低于为金属塑性模型指定的熔化温度,则硬化记忆将在退火温度下删除,熔化温度将严格用于定义硬化函数。否则,硬化记忆将在熔化温度下自动移除。如果材料点的温度在随后的时间点低于退火温度,则材料点可以再次加工硬化。同时该模型可以考虑应变率效应,即等效应力表示为
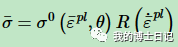
等效塑性应变表示为
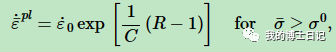
epsilon_0和C是材料参数。考虑应变率的Johnson-cook塑性本构模型可以写为
以上塑性本构模型可以在显式和隐式中进行定义,但动态失效模型仅在显式求解器中提供,该模型仅适用于金属的高应变率变形,Johnson-cook动态失效模型,基于单元积分点处的等效塑性应变值;假设当损伤参数超过1时发生失效。损伤参数ω定义为:
其中分子表示等效塑性应变增量,分母表示失效对应的应变,其中失效塑性应变,失效应变取决于应力三轴度,温度,和应变速率。即
其中d1–d5是在转变温度或低于转变温度时测量的失效参数。该模型最适用于真正动态的情况。对于需要移除元件的准静态问题,建议使用渐进损伤和破坏模型(渐进损伤和失效)或Gurson金属塑性模型(多孔金属塑性),使用该损伤模型时需要配合对应的塑性和硬化模型。
其中塑性模型相关的材料参数拟合可以参考网址:
abaqus中Johnson-Cook本构模型理解 - 知乎 (zhihu.com)
损伤相关参数拟合可以参考网址:
abaqus中Johnson-Cook损伤失效模型 - 知乎 (zhihu.com)
umat子程序验证
相同材料参数下,使用编写的umat子程序与显式求解器内置的模型进行对比,模型材料参数取自文献
模型尺寸为10*10*50(mm),沿着Z方向进行20%的拉伸。
材料参数分别为
杨氏模量:209Gpa
泊松比:0.29
塑性产热分数:0.9
材料参数A:380
材料参数B:1200
材料参数C:0.012
材料参数m:2.5
材料参数n:0.55
材料参数epsilon_0:1.0
转变温度Tr:293K
熔融温度Tm:2150K
材料参数d1-d5:0.1,0.7,1.5,0.005,0.84
模拟的结果
变形后显式与隐式结果的应力分布:
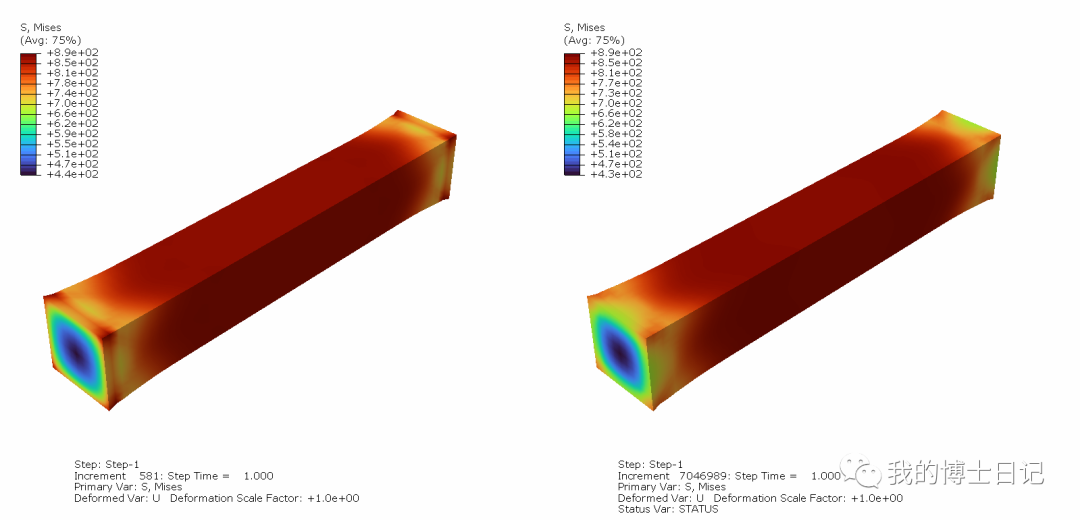
变形后显式与隐式结果的等效塑性应变分布:

可以看到显式与编写的隐式umat子程序具有良好的一致性,其中隐式计算需要大概600个增量步,而显式则需要700万的增量步,计算效率更高,但在高速冲击,切屑问题更建议使用显式程序进行计算





