结构有限元计算中的应力奇异原因剖析

1.应力奇异特征

下面通过一个计算实例，来说明应力奇异的特征，如图1所示给出了一个L型平面应变计算模型。

图1 计算模型

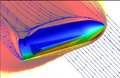
图2 初始网格计算得到的等效应力云图

如图2所示给出了，初始网格计算得到的等效应力云图，最大等效应力为41.9MPa。如图3给出了网格密度与最大等效应力的关系，由该关系可以看出，最大应力随着网格密度的增加而增加，不会达到一个稳定值。

图3 最大等效应力与节点数量的关系曲线

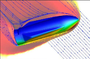
图4 加密10次后的等效应力云图

如图4所示，给出了网格加盟10次后的等效应力，通过实例计算得到规律可知，应力奇异的特征就是随着网格加密（单元尺寸减小），等效应力的数值不断增加，即最大等效应力随着网格密度增加，而不断增加，没有稳定值，理论上，应力会随着单元尺寸趋于0而趋于∞大。但是实际产品中的应力都是有限值，不会出现应力奇异。所以，应力奇异是一种数值计算的虚假解。

2.应力奇异产生的原因

（1）式中给出了应力的基本定义：

                            （1）

由公式（1）可知，如果力的作用面积趋于0，则对应的应力会趋于无穷，这个就是有限元发生奇异的本质原因，即在有限元计算中，如果存在力的作用面积趋于0，则该位置即为应力奇异位置。此外还一种情况，就是在装配体计算中，不同材料部件的绑定连接位置也是一个应力奇异发生的位置，因为这个地方的应力是跳跃的，不连续的，从而导致奇异。

3.产生应力奇异的常见位置

应力奇异发生的位置，就是力的作用面积趋于0的位置，主要包括如下几种常见位置：

（1）直角位置（如前所示）；

（2）集中力载荷作用的点线位置。

（3）固定约束位置的节点；

（4）材料突变或绑定连接的界面位置；